Эффективное использование алгоритма Флойда в ориентированных графах

Алгоритм Флойда является одним из ключевых методов для нахождения кратчайших путей во всех парах вершин ориентированного графа. Он широко используется в различных областях, включая компьютерные сети, геоинформационные системы и анализ данных. В этом разделе вы найдете подборку фотографий и полезные советы по использованию алгоритма Флойда для работы с ориентированными графами.

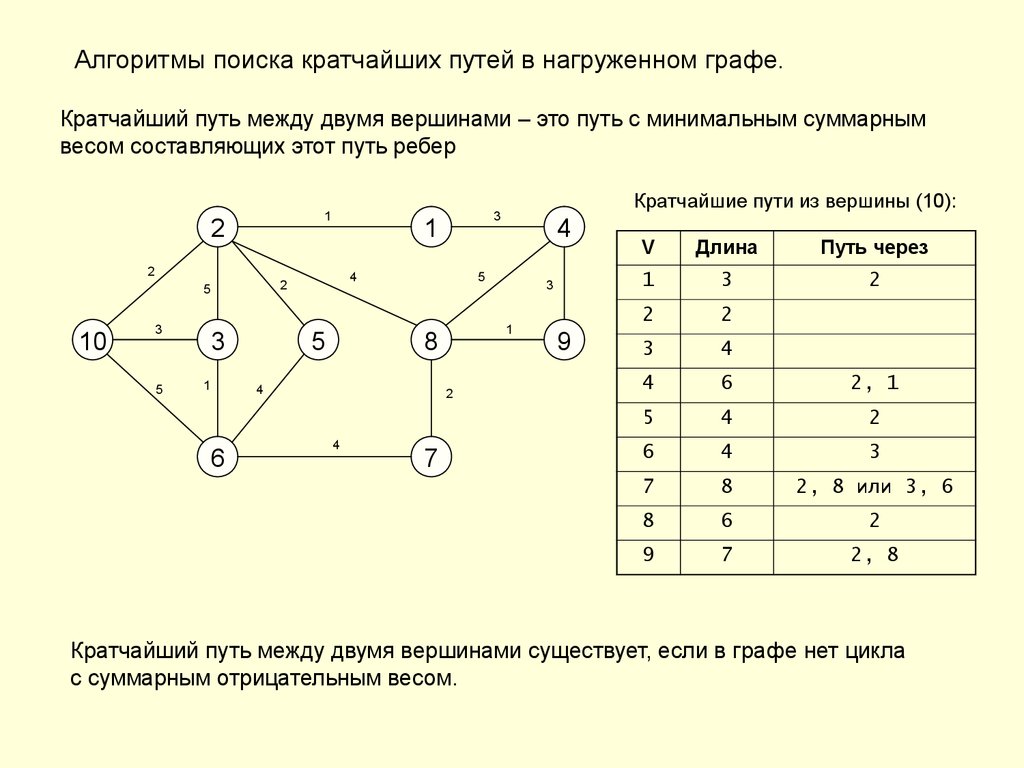
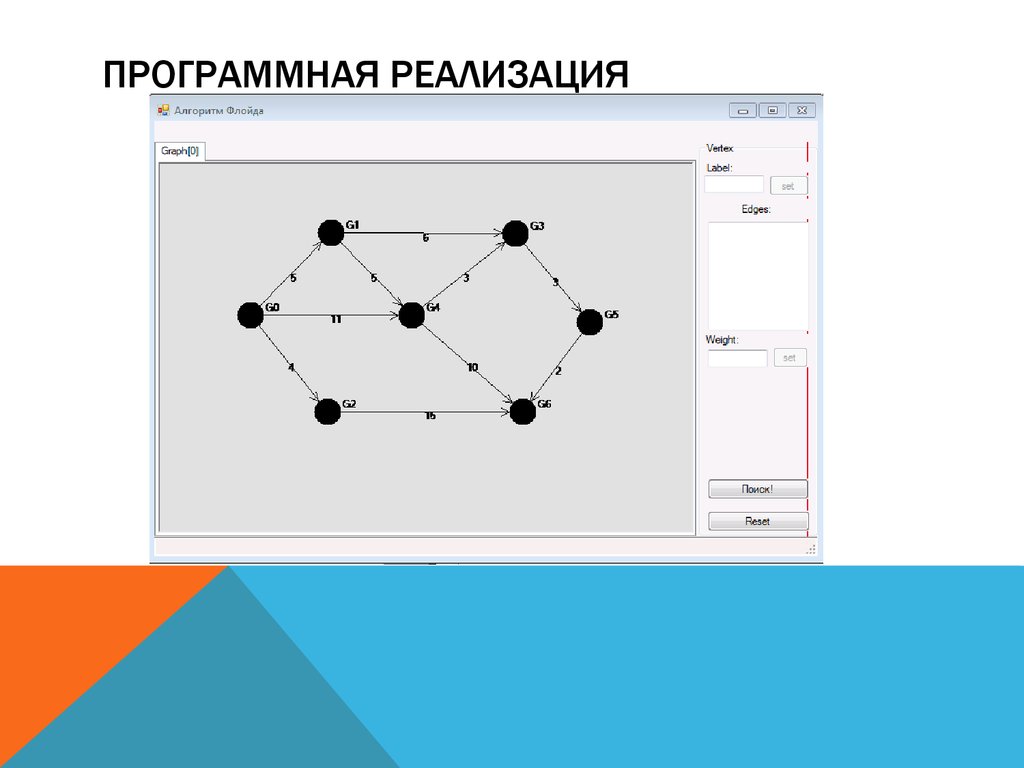
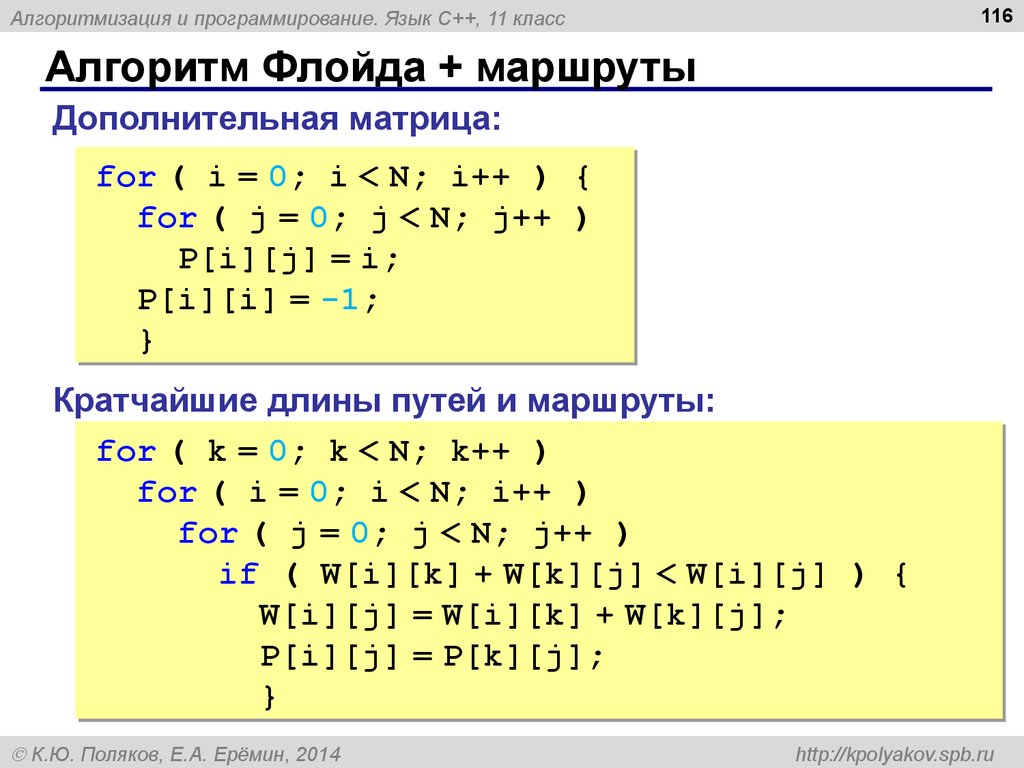
Проверьте, чтобы все вершины и ребра графа были корректно заданы перед запуском алгоритма Флойда.

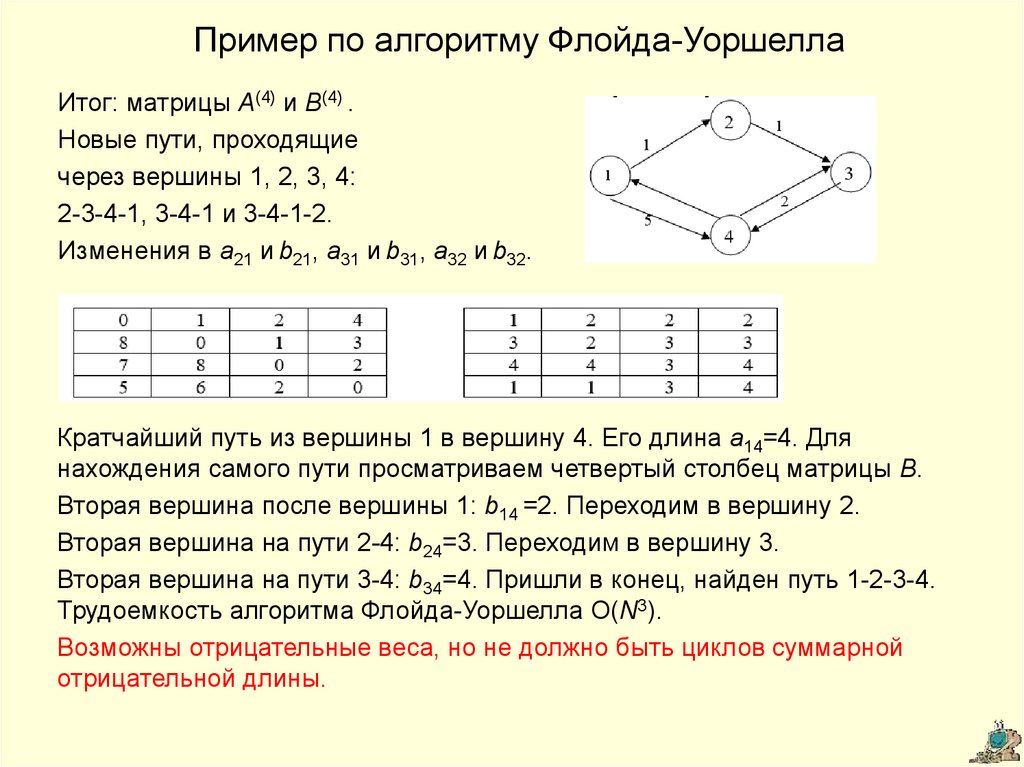
Используйте матрицу смежности для представления графа, так как это облегчит вычисления алгоритма Флойда.

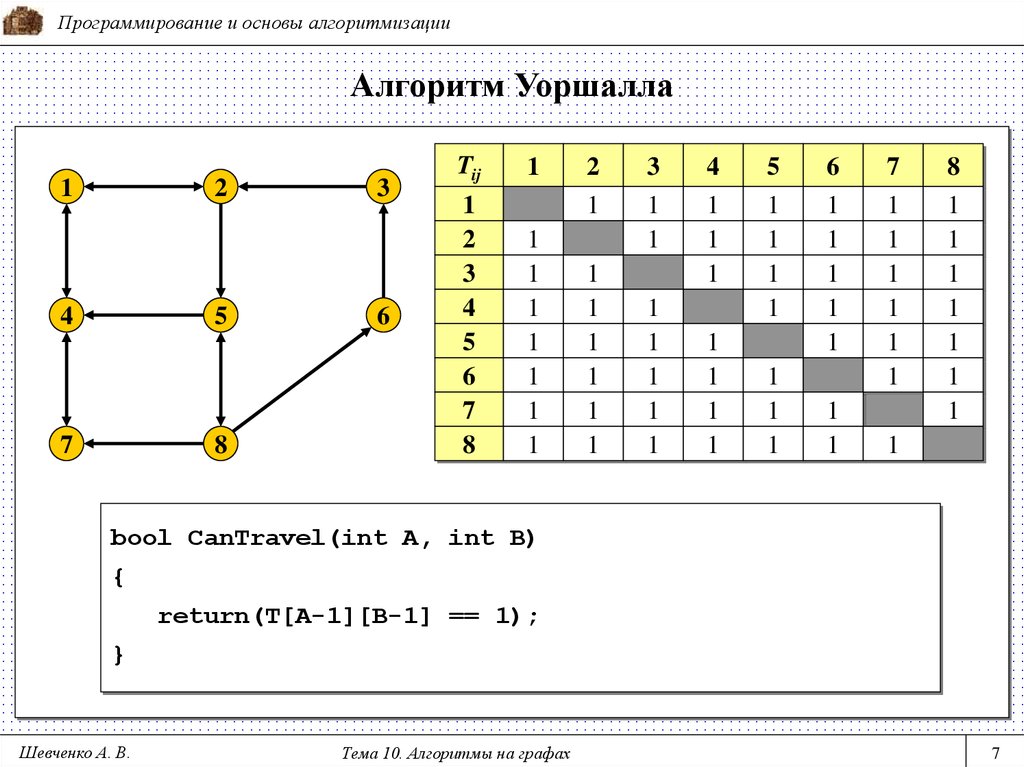
Не забывайте о необходимости обновления матрицы расстояний на каждом шаге алгоритма.

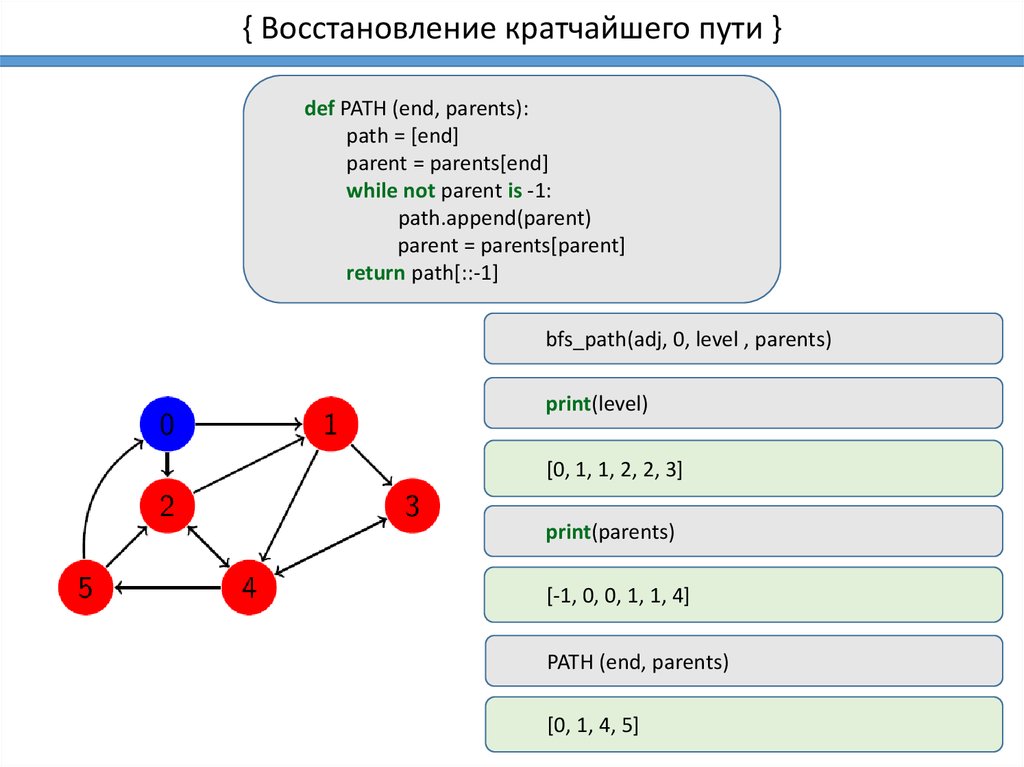
Алгоритм Флойда работает за O(n^3) времени, поэтому для очень больших графов рассмотрите другие оптимизации или алгоритмы.

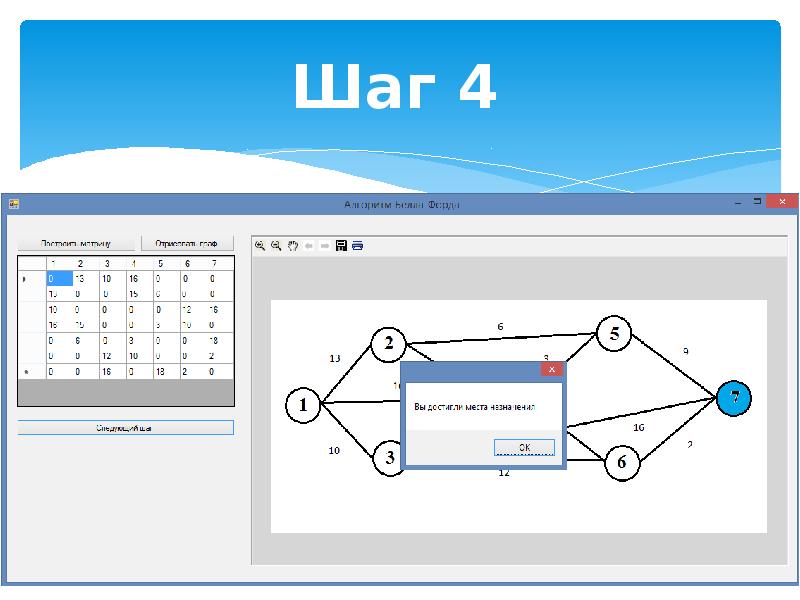
В случае наличия отрицательных циклов в графе, алгоритм Флойда может не дать корректных результатов. Проверьте граф на наличие таких циклов заранее.

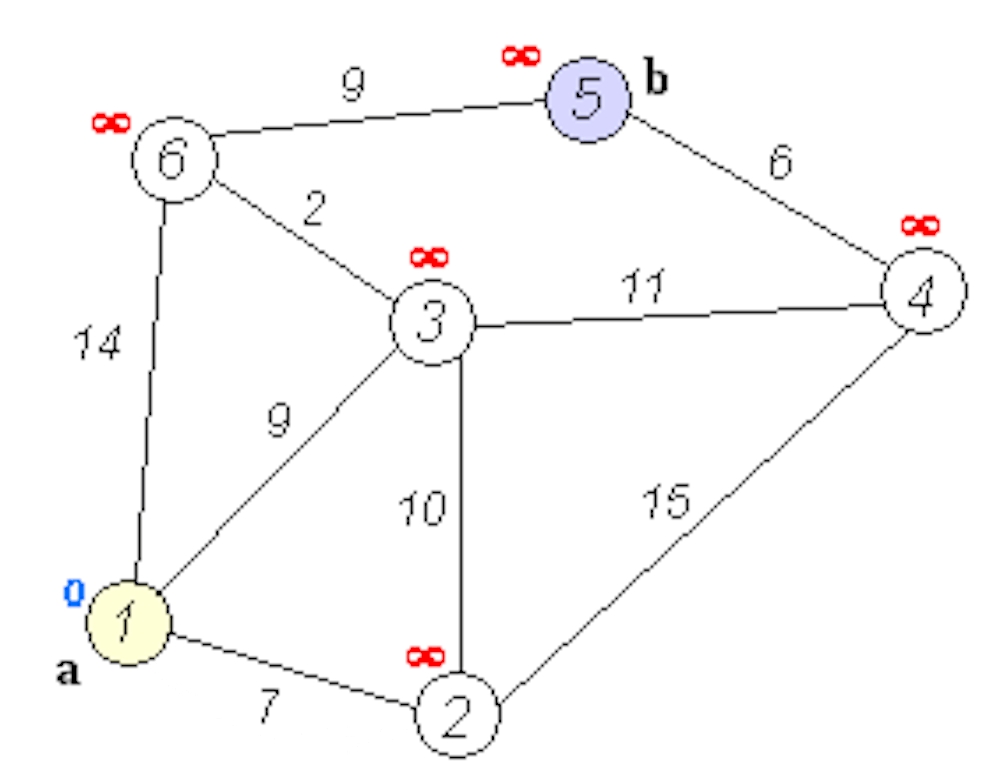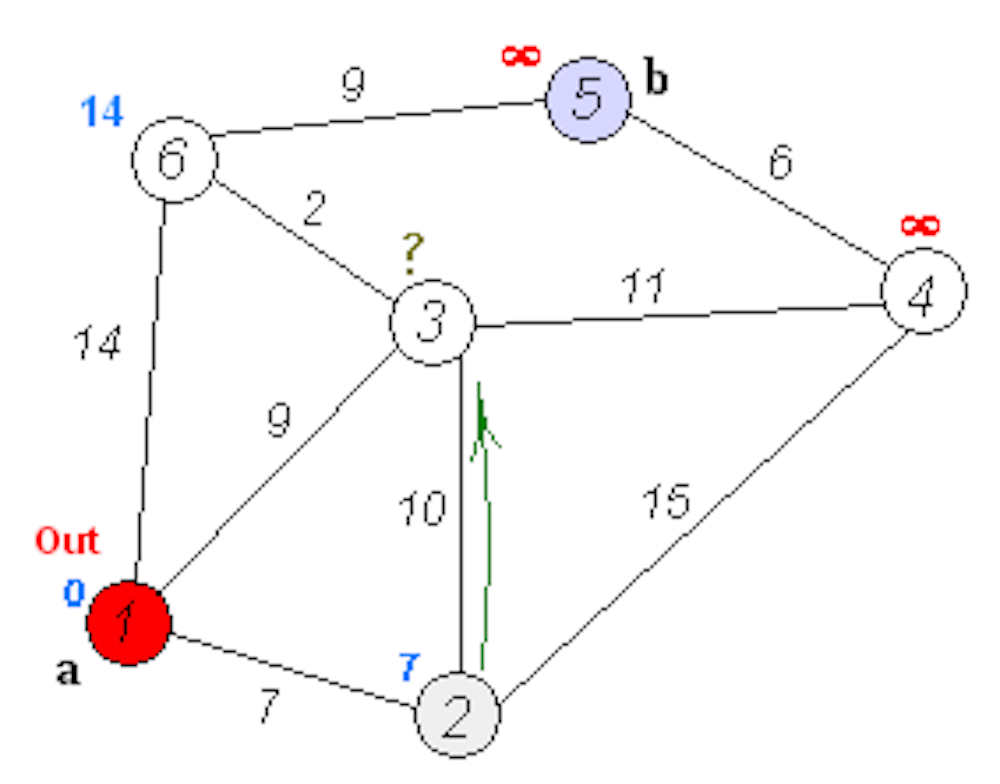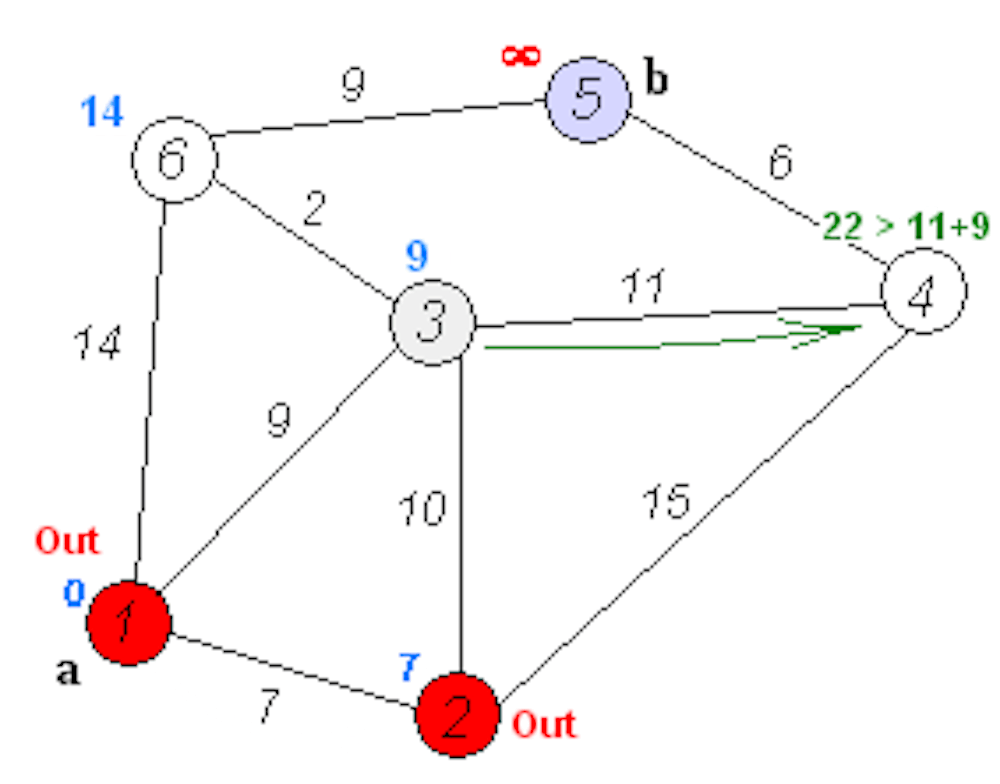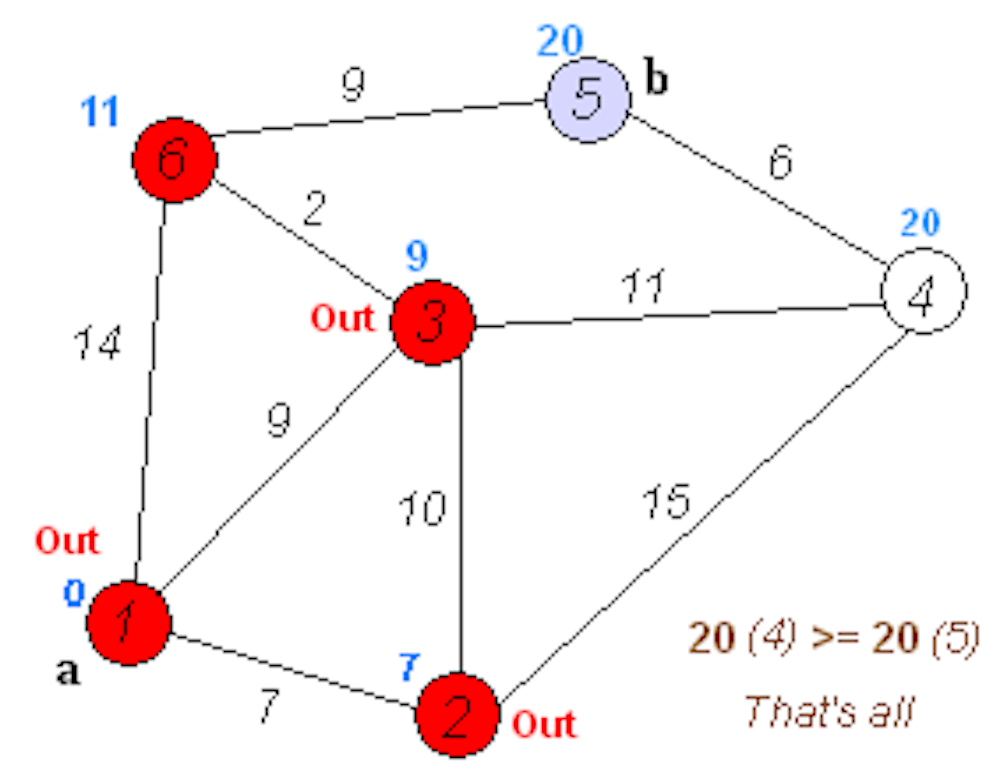
Алгоритм Флойда применим как для взвешенных, так и для невзвешенных графов, но для невзвешенных графов можно использовать более простые алгоритмы.

Для визуализации работы алгоритма используйте графические библиотеки, такие как Graphviz или Matplotlib.

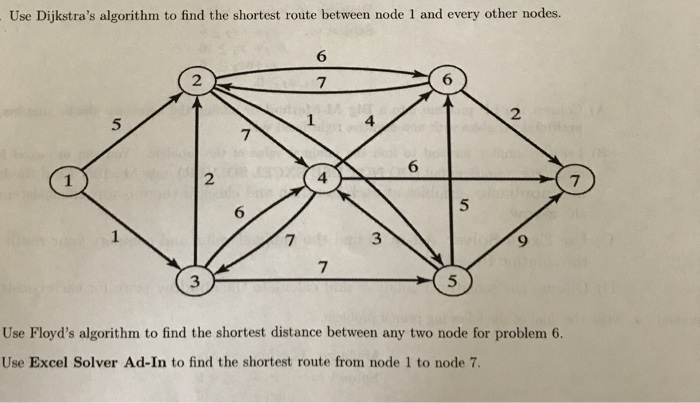
Храните промежуточные результаты работы алгоритма, чтобы иметь возможность восстановить путь между любыми двумя вершинами.

Сравните результаты работы алгоритма Флойда с другими алгоритмами, такими как Дейкстра или Беллмана-Форда, чтобы выбрать наиболее подходящий метод для вашей задачи.

При разработке программного обеспечения используйте тестовые данные для проверки корректности реализации алгоритма Флойда.