Простой способ доказательства признака вписанного четырехугольника

На этой странице вы найдете подборку фотографий и полезные советы по доказательству признака вписанного четырехугольника. Узнайте, как легко и эффективно применить теоретические знания на практике.

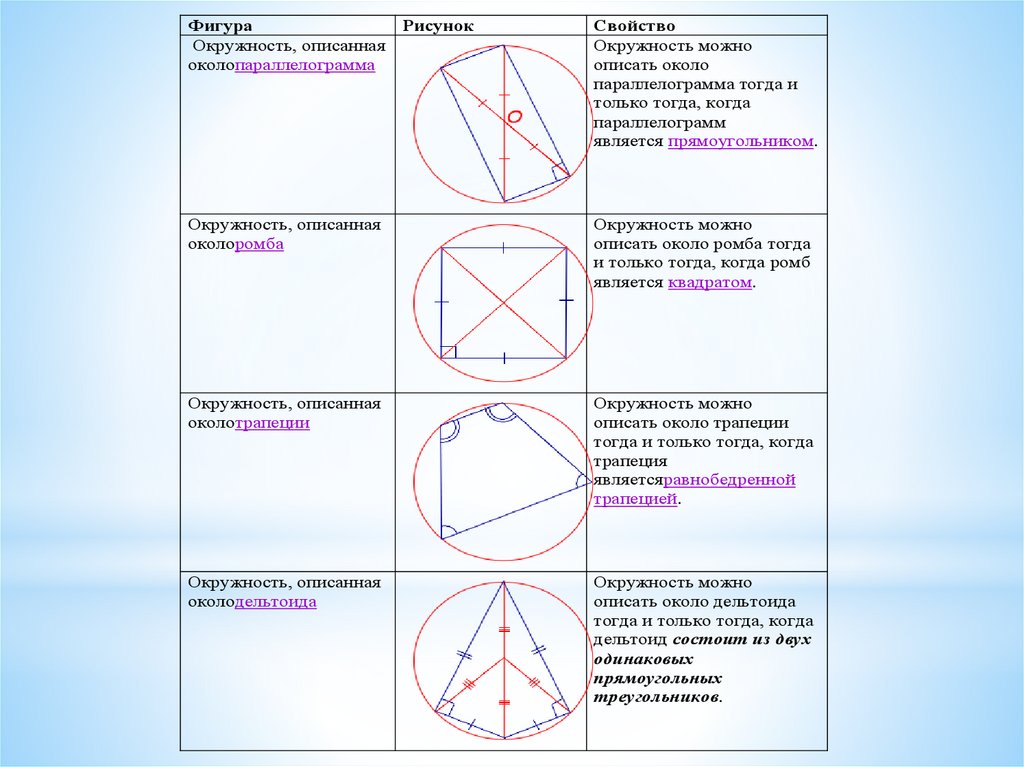
Начните с определения вписанного четырехугольника: это четырехугольник, все вершины которого лежат на одной окружности.

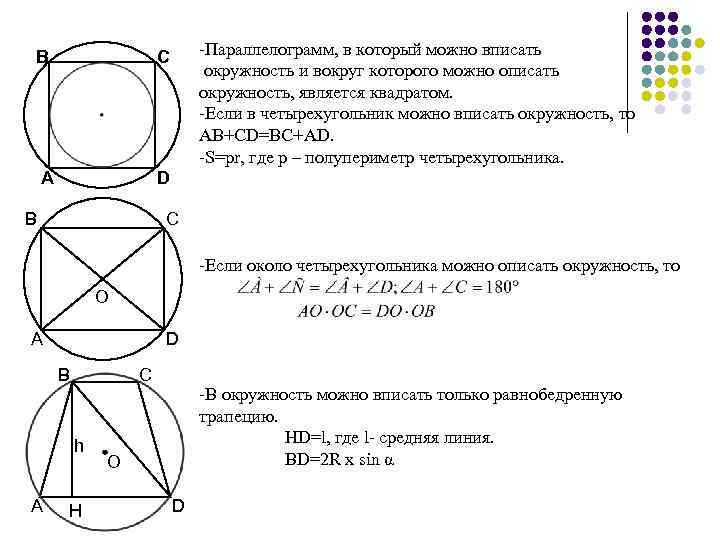
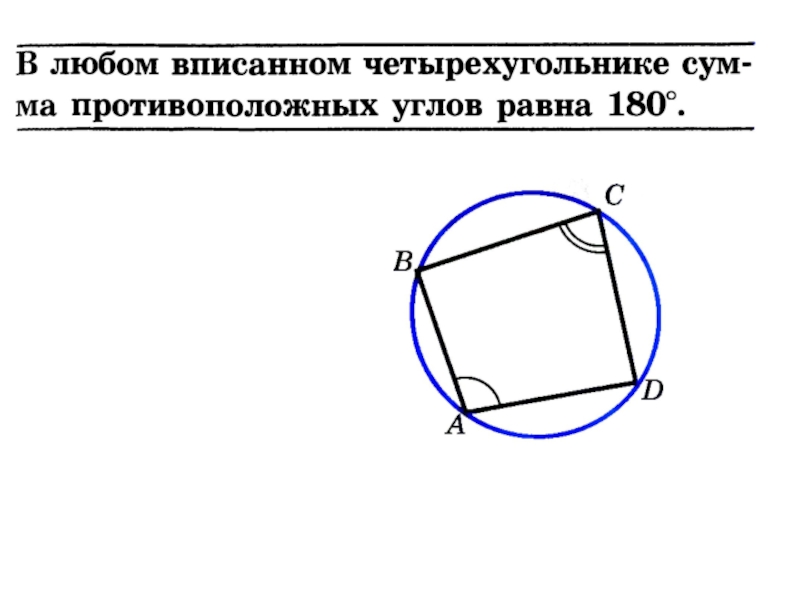
Используйте теорему о вписанных углах: сумма противоположных углов вписанного четырехугольника равна 180 градусам.

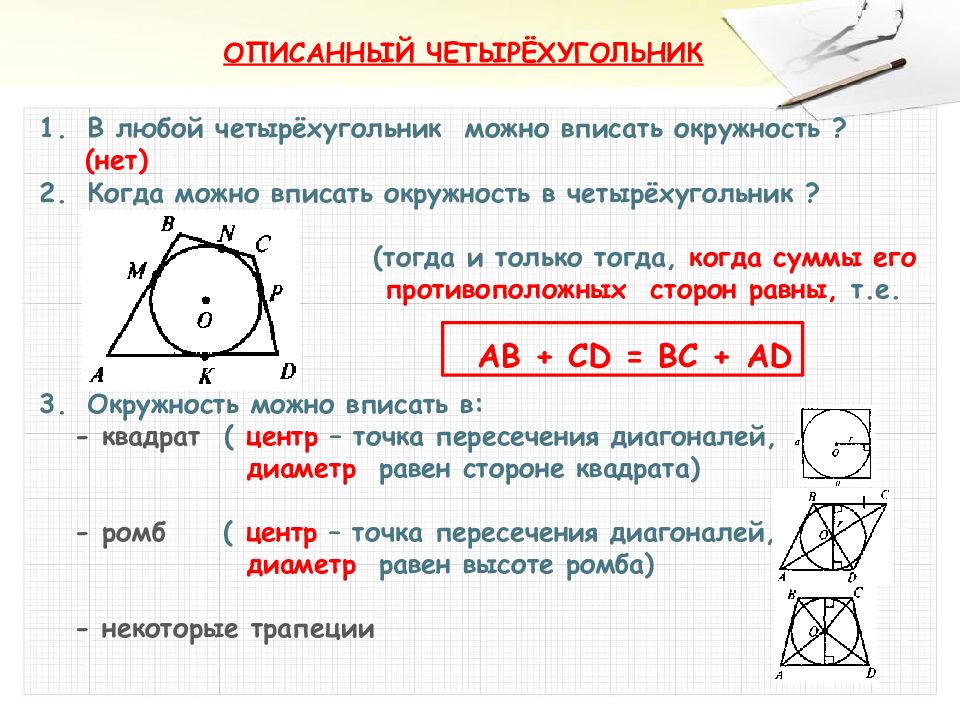
Проведите диагонали четырехугольника и убедитесь, что они пересекаются в одной точке, лежащей на окружности.

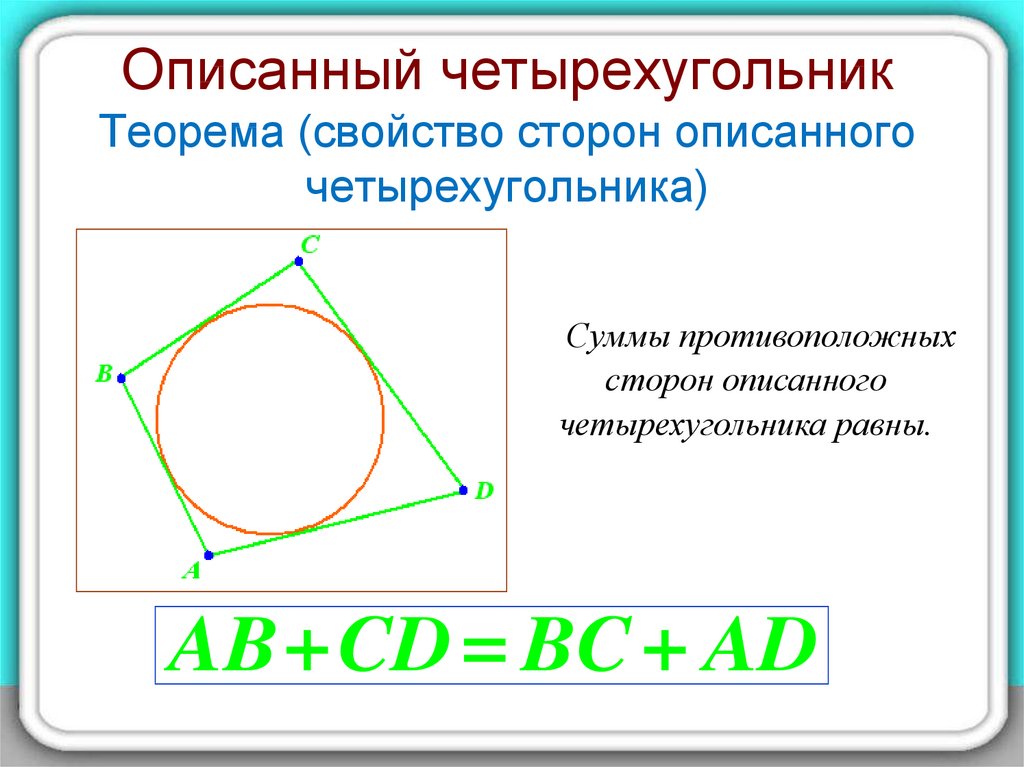
Проверьте, что произведение длин противоположных сторон вписанного четырехугольника равно произведению длин его диагоналей.

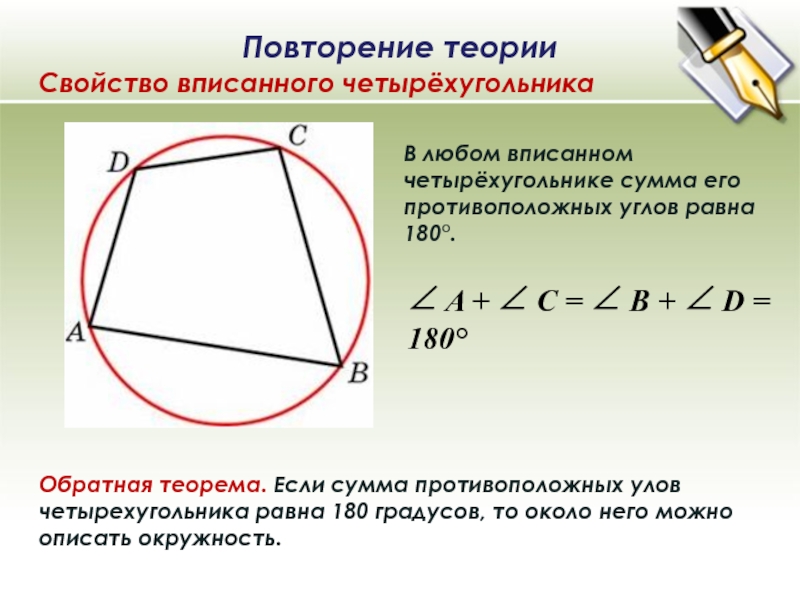
Используйте косинусную теорему для проверки сумм углов между диагоналями и сторонами четырехугольника.

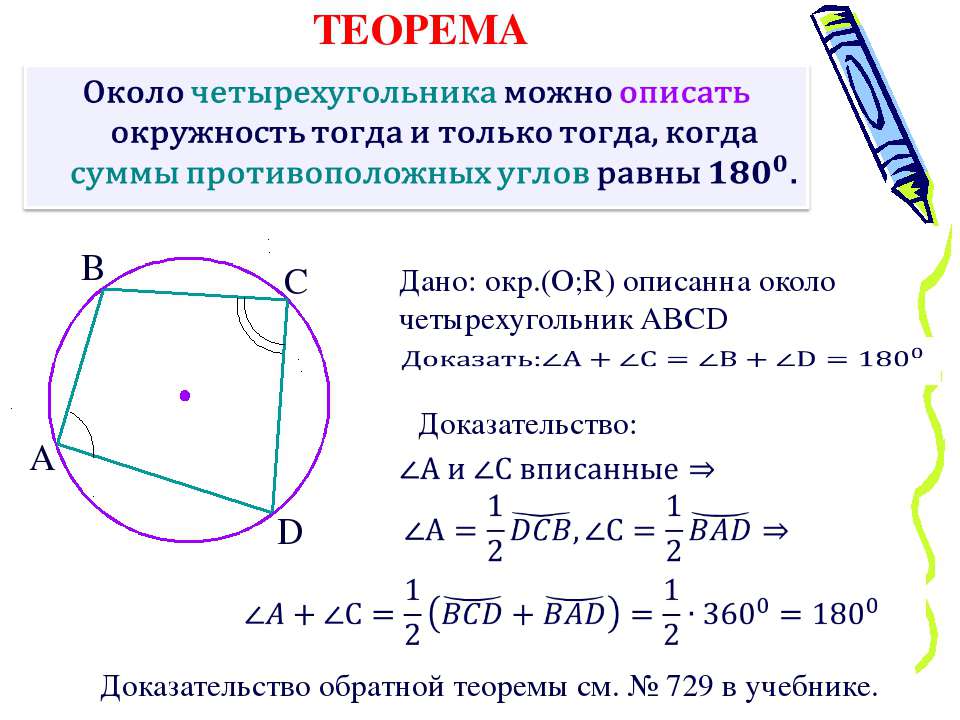
Для сложных случаев применяйте метод координат, чтобы доказать, что все вершины четырехугольника имеют одинаковое расстояние до центра окружности.

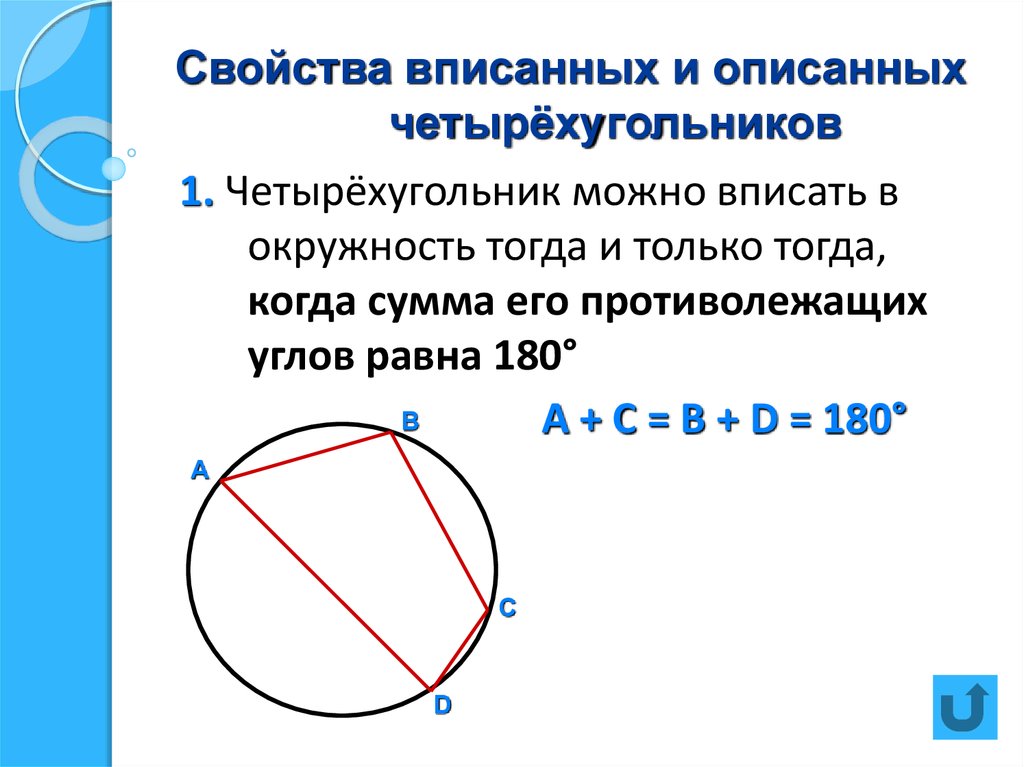
Используйте графические методы: нарисуйте четырехугольник и окружность, чтобы наглядно видеть взаимное расположение вершин.

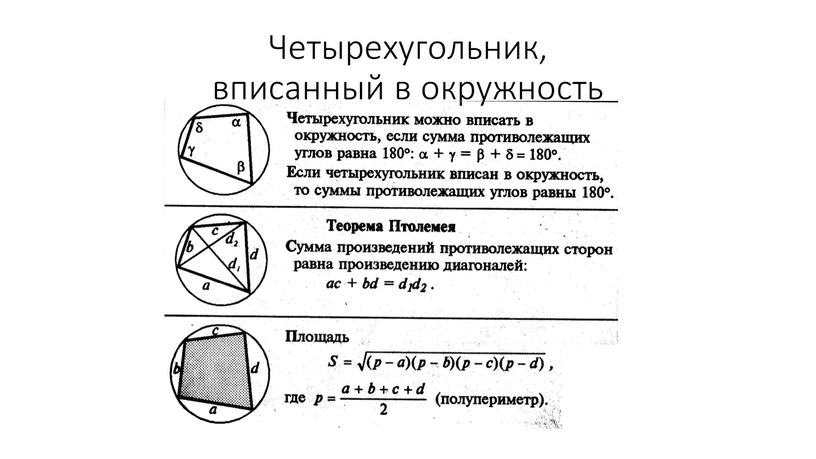
Рассмотрите частные случаи: равнобедренные трапеции и прямоугольники, которые всегда являются вписанными четырехугольниками.

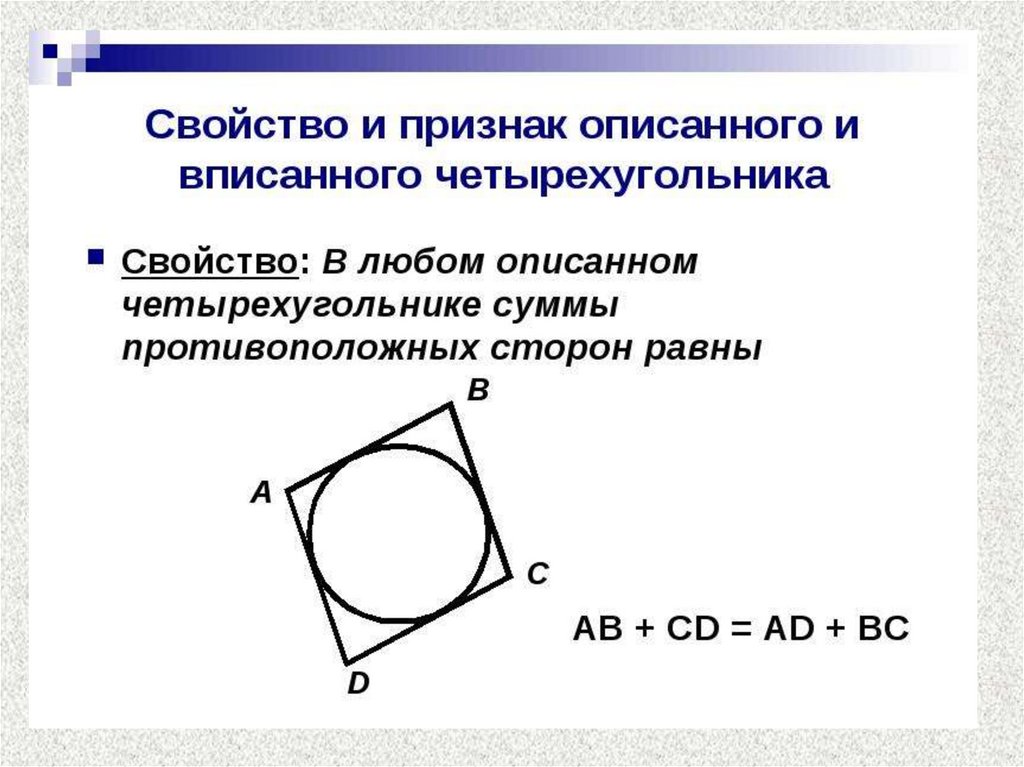
Используйте динамические геометрические программы, такие как GeoGebra, для визуализации и проверки своих гипотез.

Проводите практические занятия с использованием реальных объектов, например, рисунков на бумаге или моделирования с помощью конструктора.