Как правильно применять формулы прямой и обратной пропорциональности

На этой странице вы найдете полезные советы и примеры применения формул прямой и обратной пропорциональности. Эти формулы являются важными инструментами для решения различных математических задач и часто встречаются в учебных материалах. Мы предлагаем подробные объяснения и практические рекомендации, которые помогут вам лучше понять и использовать эти концепции.

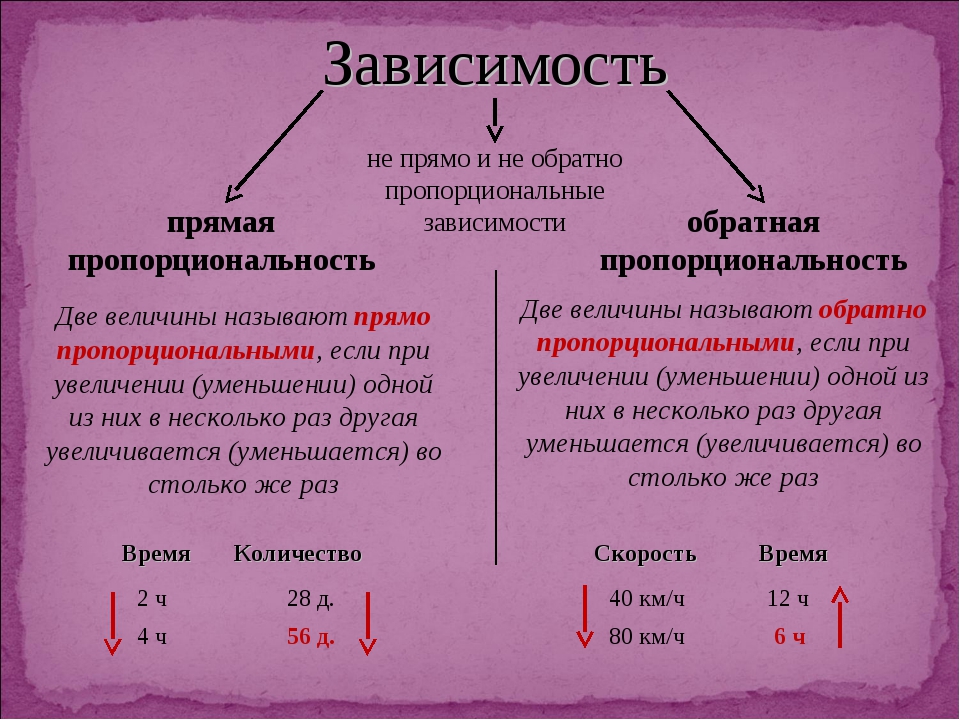
Для формулы прямой пропорциональности используйте равенство вида y = kx, где k — коэффициент пропорциональности. Это означает, что с увеличением x y также увеличивается в пропорциональном соотношении.

Для формулы обратной пропорциональности используйте равенство вида xy = k, где k — постоянное значение. Это означает, что при увеличении x значение y уменьшается пропорционально, и наоборот.

Для решения задач на прямую пропорциональность сначала определите коэффициент пропорциональности k, используя данные из задачи. Затем применяйте эту величину для нахождения искомых значений.

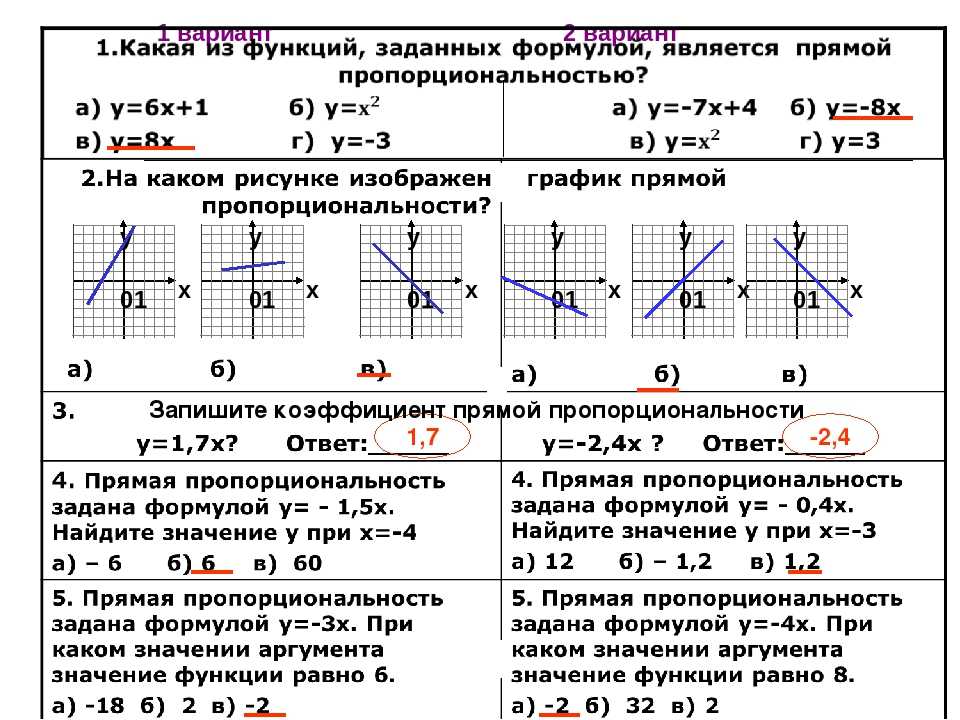
Для задач на обратную пропорциональность сначала найдите постоянное значение k, умножив известные значения x и y. Затем используйте это значение для расчета новых переменных.

В задачах на пропорциональность всегда проверяйте, правильно ли определены пропорции. Ошибка в определении пропорций может привести к неверным результатам.

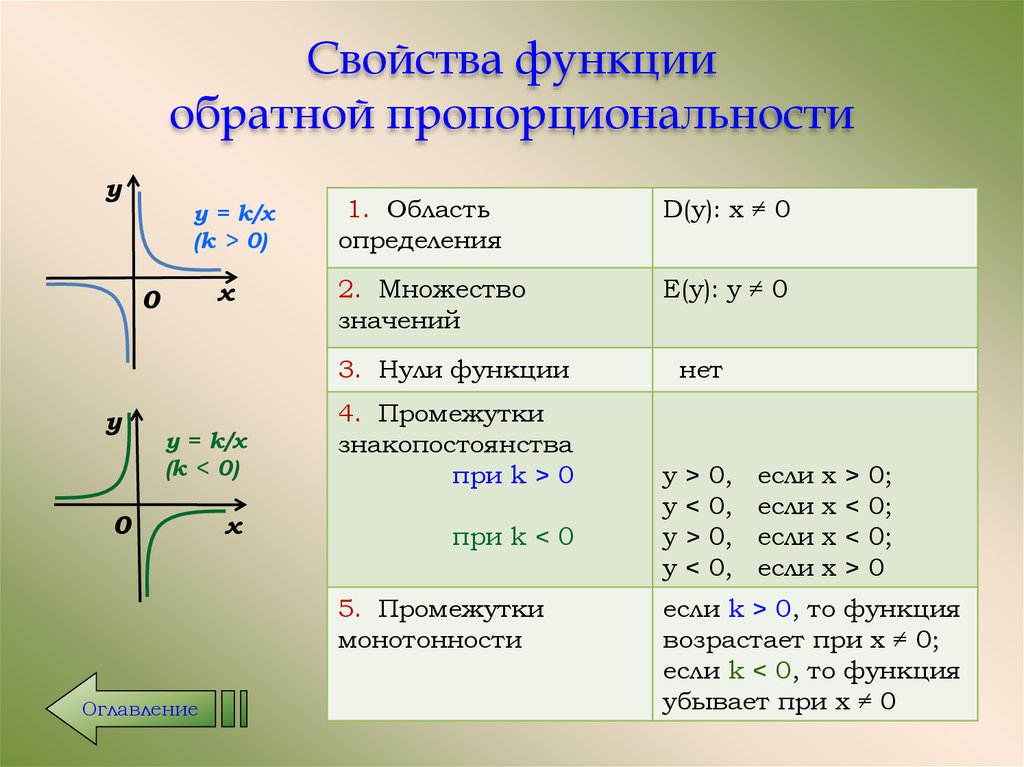
Используйте графики для визуализации прямой и обратной пропорциональности. Это может помочь лучше понять зависимость между переменными.

При решении задач с несколькими пропорциями составьте систему уравнений, чтобы упростить расчет и избежать ошибок.

Обращайте внимание на единицы измерения в задачах на пропорциональность. Несоответствие единиц может привести к неверным результатам.

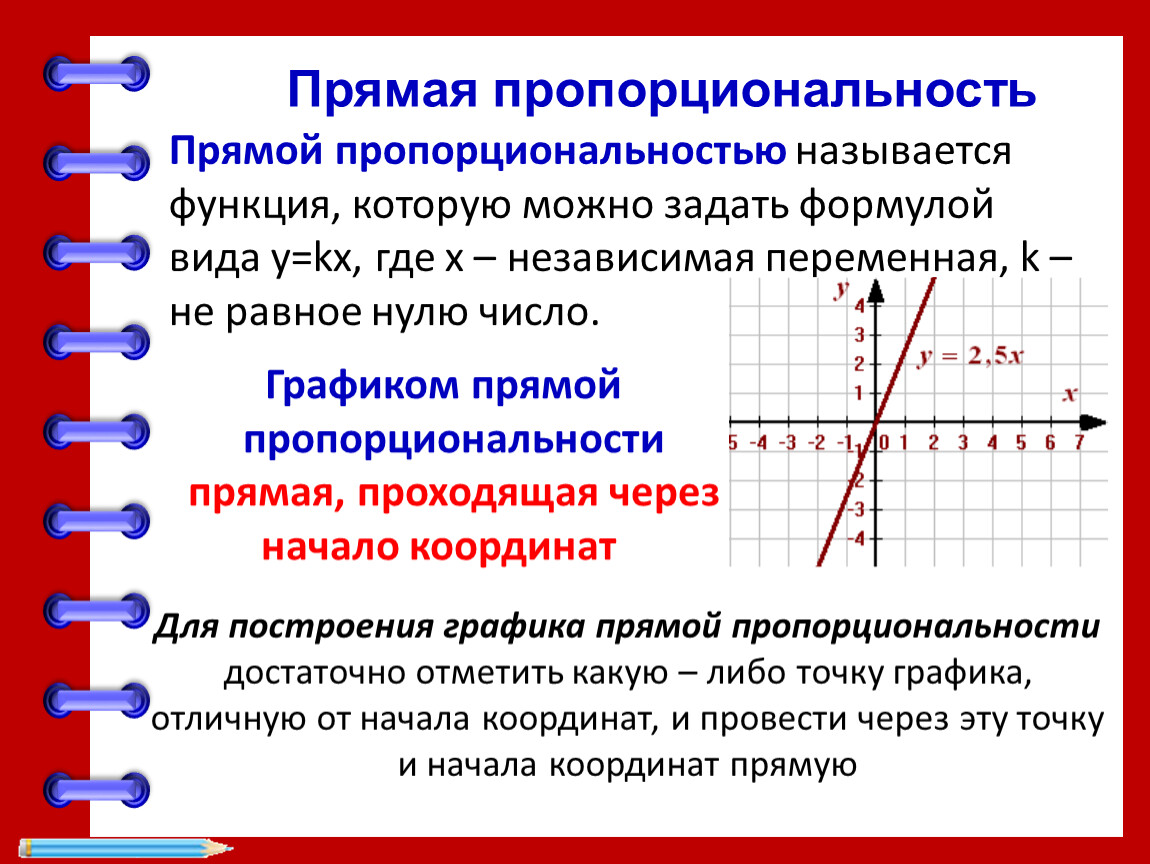
Практикуйтесь в решении задач на пропорциональность, чтобы лучше запомнить формулы и методы их применения.

Используйте калькулятор для проверки промежуточных вычислений, чтобы избежать арифметических ошибок при решении задач.