Путеводитель по обозначениям числовых множеств: от простых чисел до комплексных

На этой странице вы найдете подборку фотографий и полезные советы, связанные с обозначением различных числовых множеств, таких как натуральные числа, целые числа, рациональные и иррациональные числа, а также комплексные числа. Мы рассмотрим символы и нотации, используемые для каждого множества, и дадим практические советы для их запоминания и использования.

Для натуральных чисел используется обозначение N, например, N = {1, 2, 3, ...}. Запомните, что они включают только положительные целые числа.

Целые числа обозначаются символом Z, где Z = {..., -2, -1, 0, 1, 2, ...}. Эти числа включают как положительные, так и отрицательные целые числа, а также ноль.

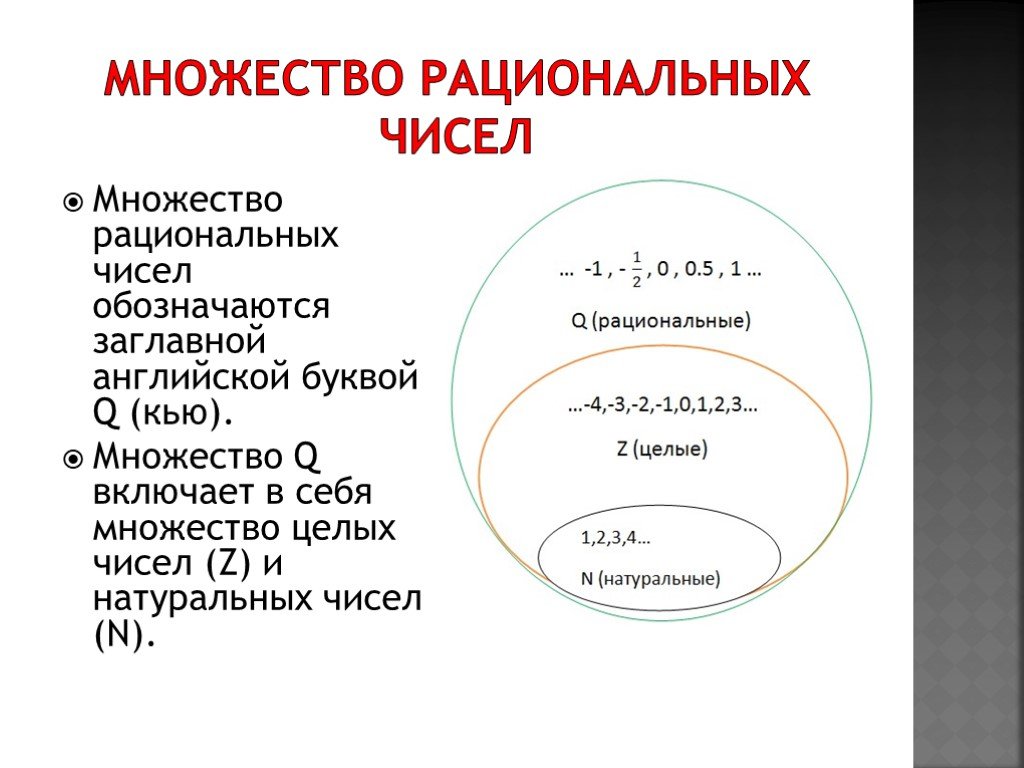
Рациональные числа, обозначаемые Q, включают все числа, которые можно представить в виде дроби m/n, где m и n - целые числа, и n ≠ 0.

Иррациональные числа не могут быть представлены в виде дроби и обозначаются как R / Q. Примеры включают числа, такие как √2 и π.

Комплексные числа обозначаются символом C и включают все числа вида a + bi, где a и b - вещественные числа, а i - мнимая единица.

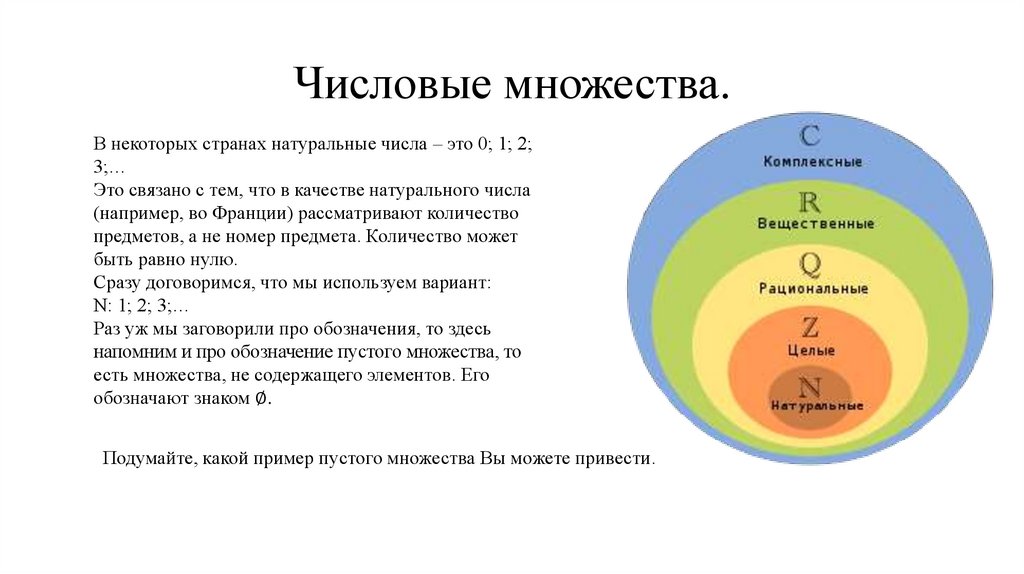
Для удобства запоминания обозначений множеств можно использовать ассоциации, например, N для натуральные, Z для целые (от немецкого Zahlen), Q для рациональные (от quotient), R для вещественные (real), C для комплексные (complex).

Используйте визуальные подсказки и схемы, чтобы лучше запомнить различия между множествами чисел и их обозначениями.

Практикуйтесь в использовании этих обозначений на примерах, решая задачи и проверяя себя.

Понимание обозначений числовых множеств поможет вам более эффективно изучать математику и физику, так как эти символы часто встречаются в учебных материалах.

Помните, что последовательное использование правильных обозначений поможет избежать путаницы и ошибок в математических выкладках и доказательствах.