Методы определения дифференциала y функции
На этой странице вы найдете полезные советы и методы, которые помогут вам определить дифференциал y у различных функций. Эти знания будут полезны как студентам, так и профессионалам в области математики и науки.
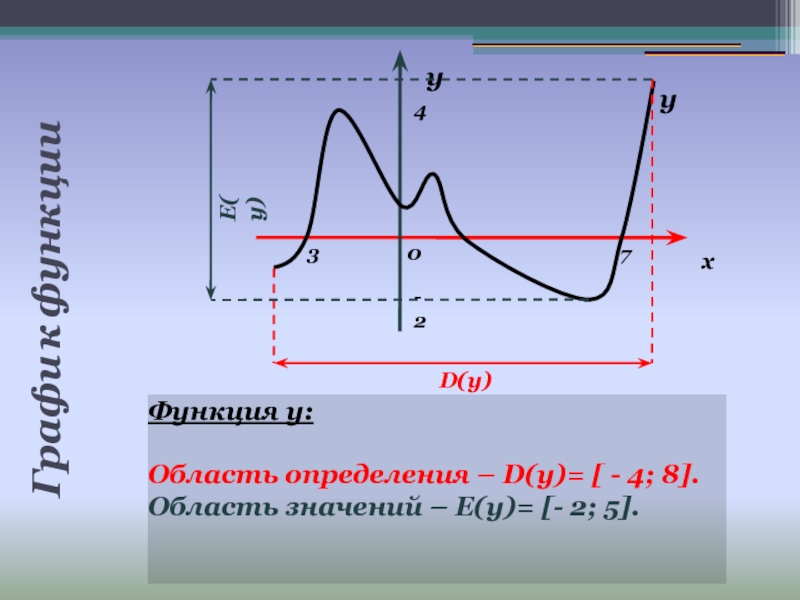
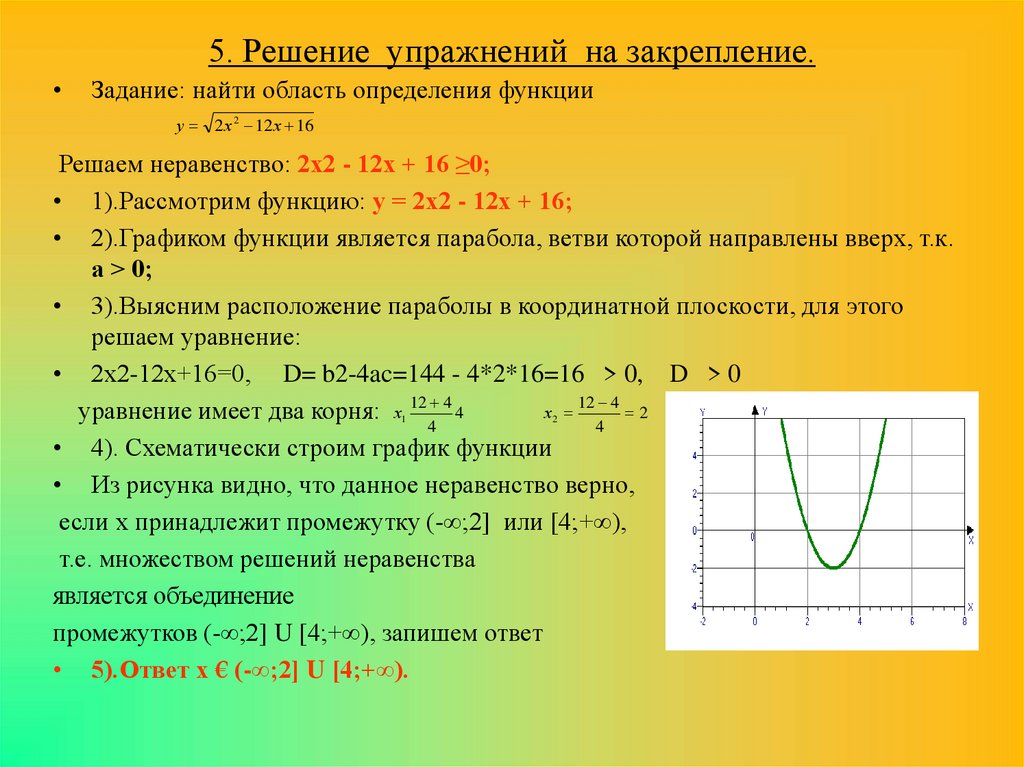
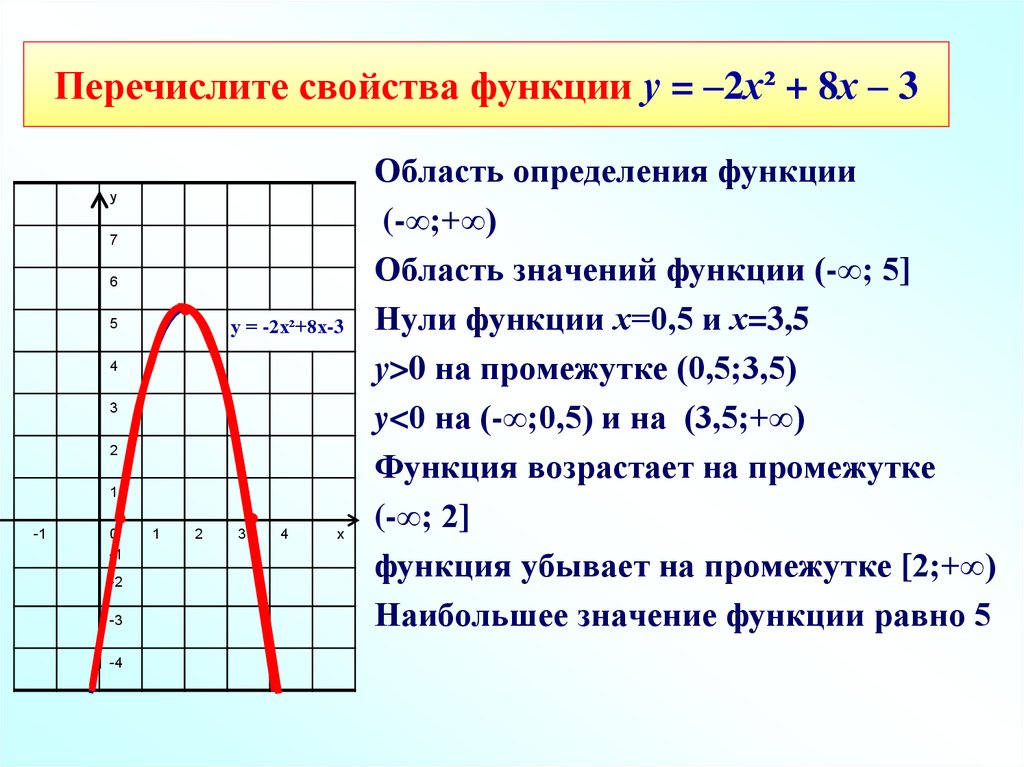
Для начала убедитесь, что функция непрерывна в той точке, где вы хотите найти дифференциал.
Область определения функций

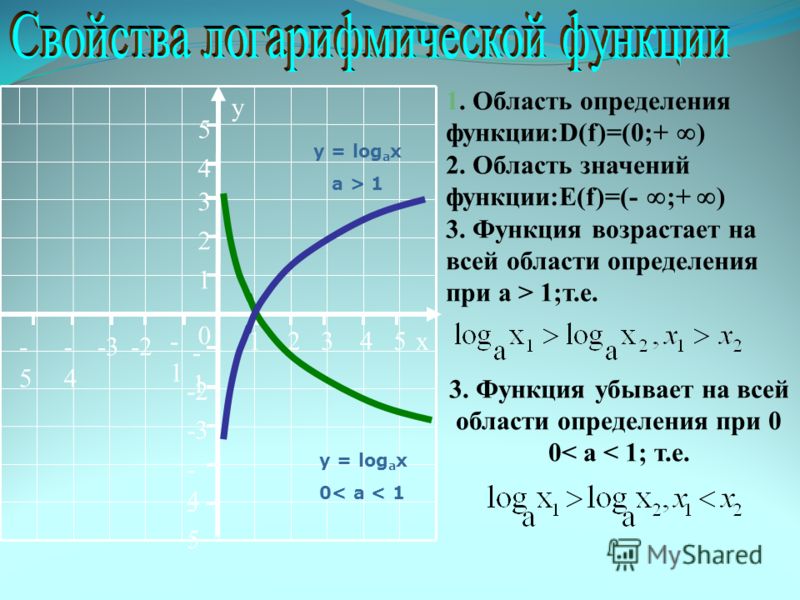
Вспомните основные правила дифференцирования, такие как правило произведения и цепное правило.

Используйте производную функции для нахождения дифференциала: dy = f(x)dx.
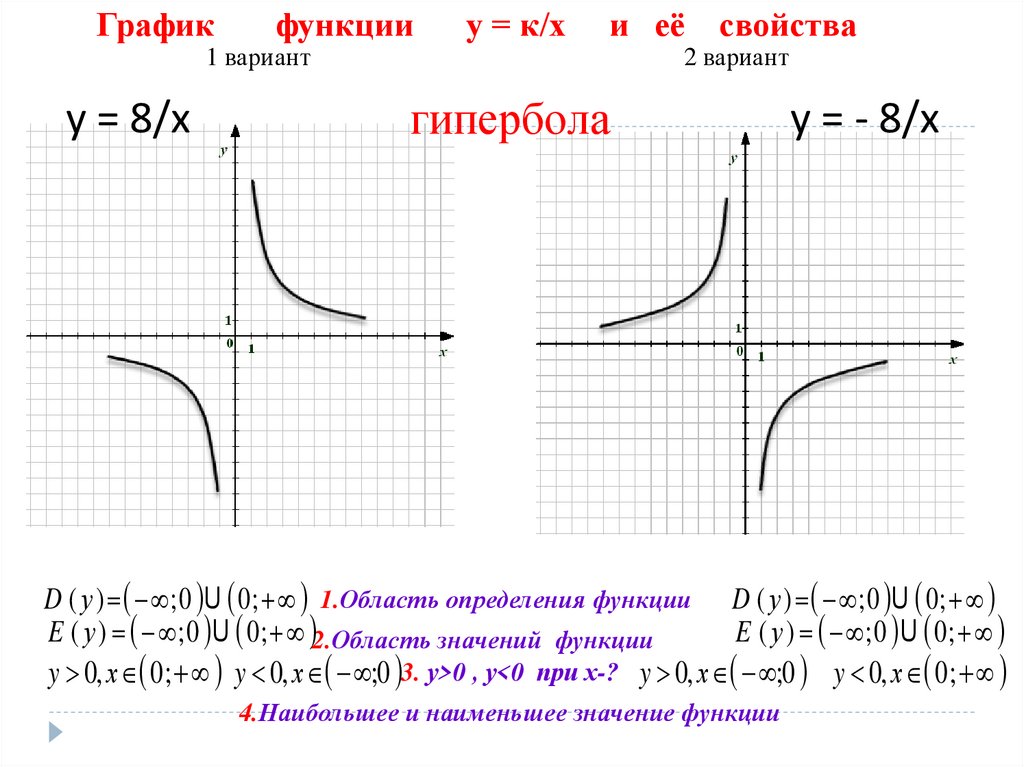
Применяйте табличные производные для стандартных функций, таких как синус, косинус, экспонента и логарифм.

При необходимости используйте подстановку для упрощения сложных функций перед дифференцированием.

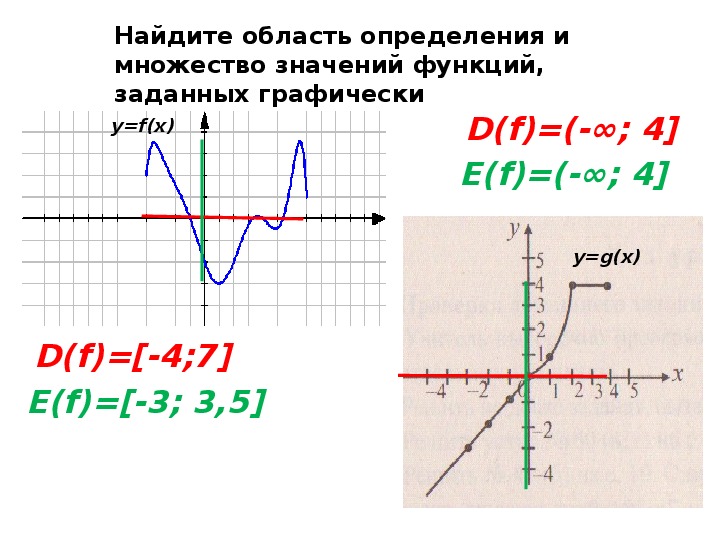
Если функция задана параметрически, используйте производные параметров для нахождения dy и dx.
Проверяйте свои результаты, используя численные методы или графические построения.
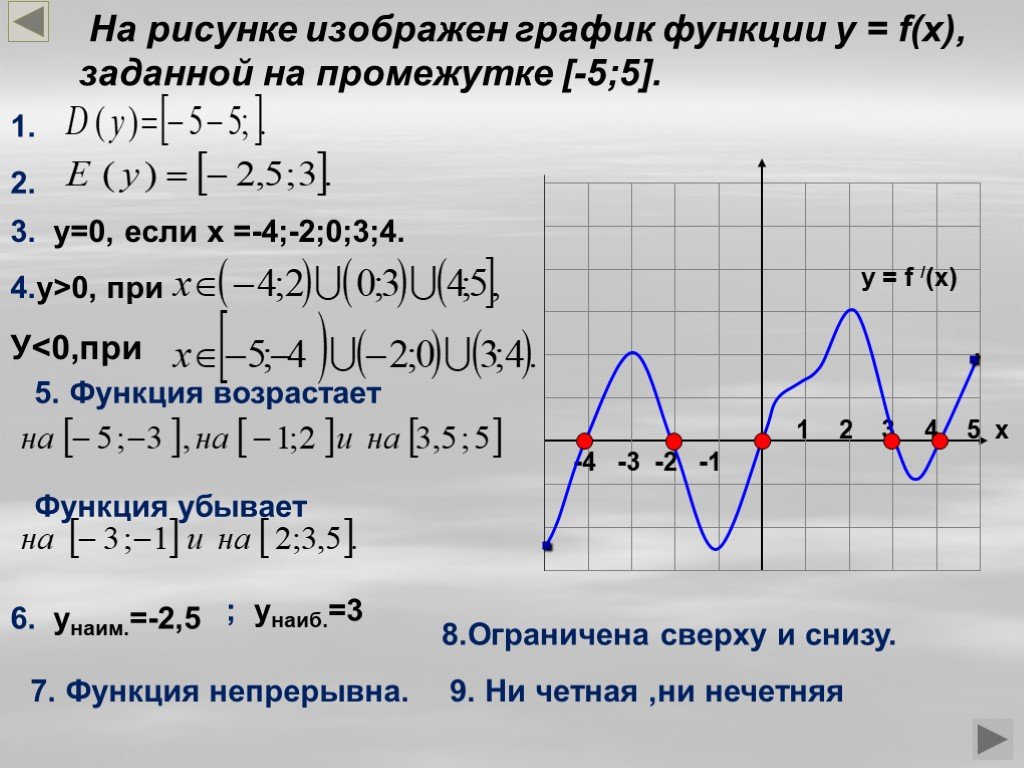
Обращайте внимание на граничные условия и точки разрыва, если они присутствуют в функции.
Помните, что дифференциал — это линейное приближение изменения функции в малой окрестности точки.
Практикуйтесь на различных типах функций, чтобы лучше понимать методы и приемы нахождения дифференциала.