Как определить критические точки функции: полное руководство
Критические точки функции играют важную роль в анализе ее поведения. Они помогают выявить локальные максимумы, минимумы и точки перегиба, что особенно важно в математическом моделировании и прикладных задачах. В этой статье мы рассмотрим, как определить критические точки функции и использовать их для анализа.
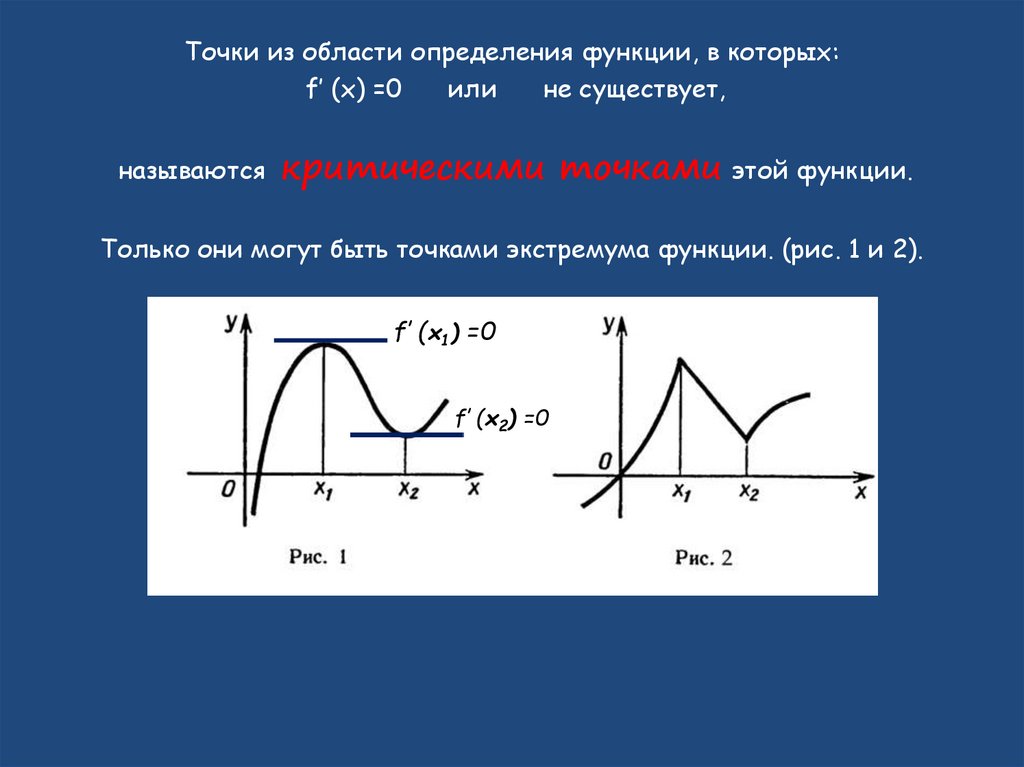

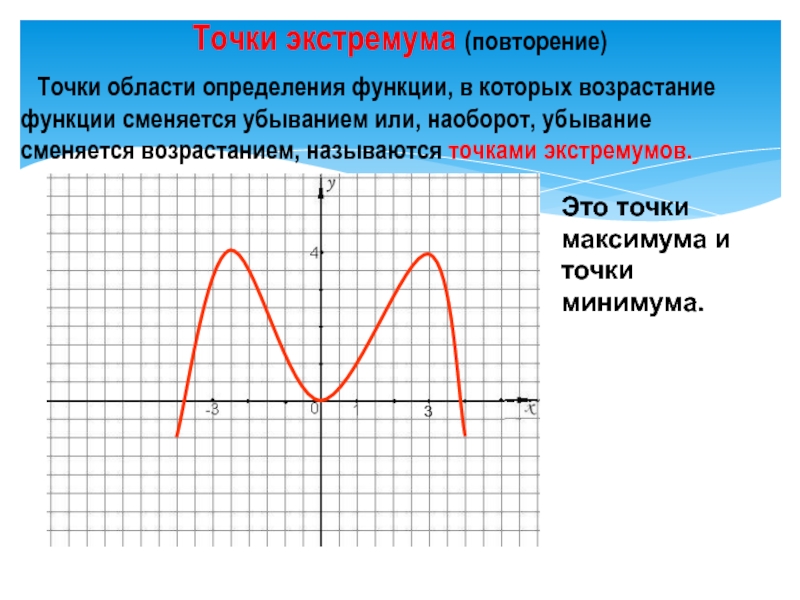
Для нахождения критических точек функции сначала нужно вычислить её производную.
Критические точки
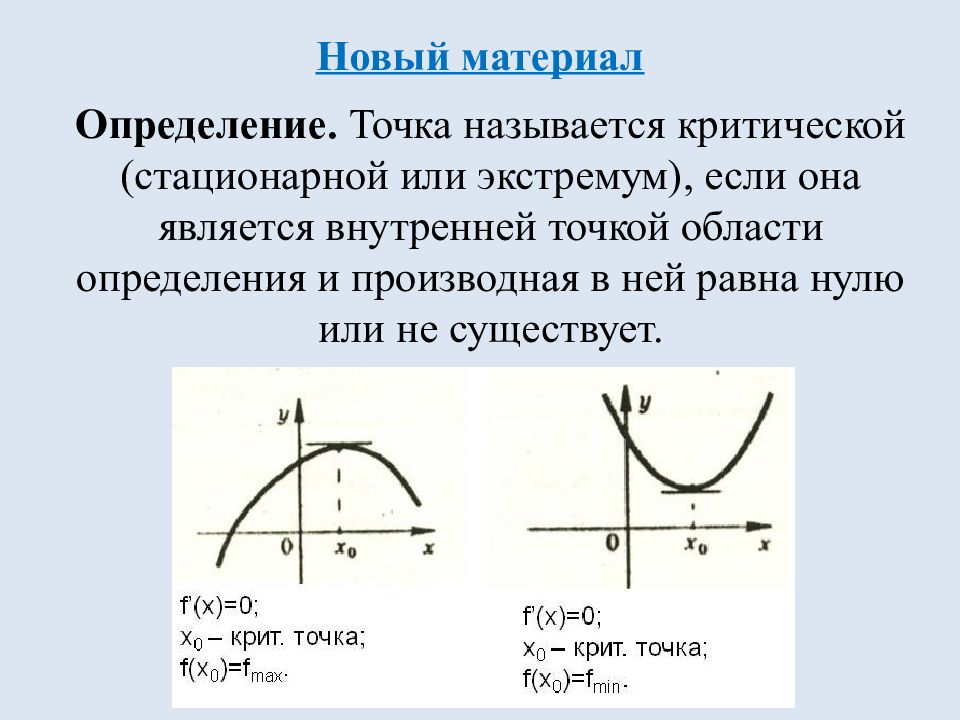
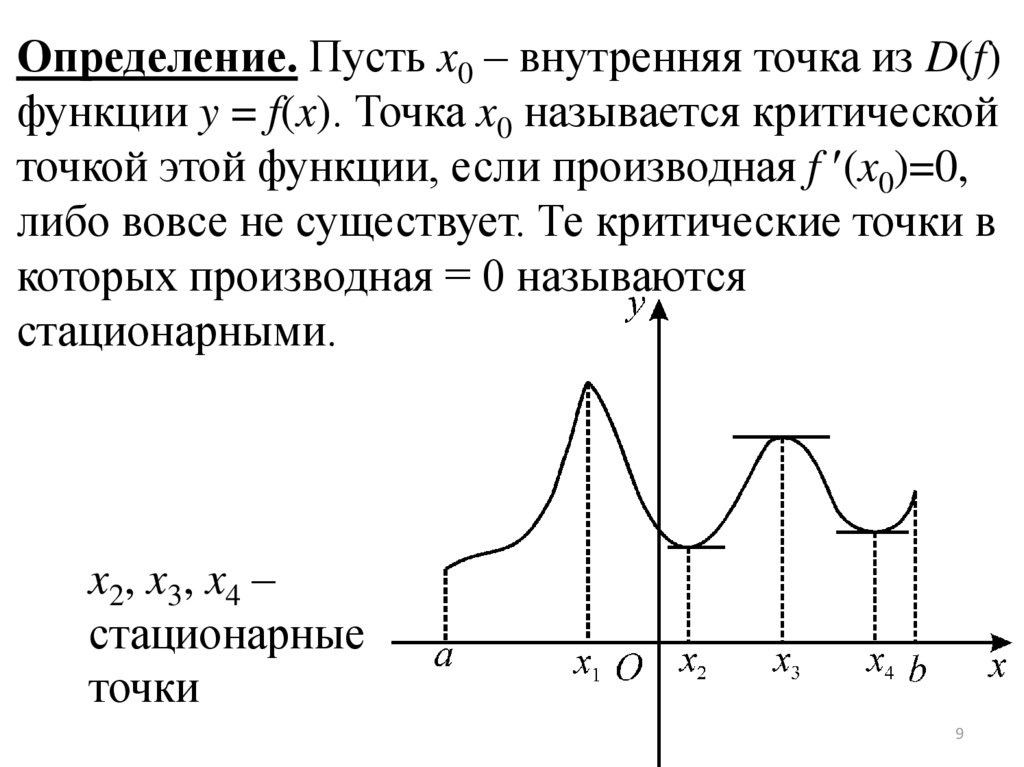
Приравняйте производную функции к нулю и решите уравнение для нахождения точек, где производная равна нулю.
АЛГЕБРА С НУЛЯ — Точки Экстремума Функции
Не забудьте также найти точки, где производная не существует, так как они также могут быть критическими точками.
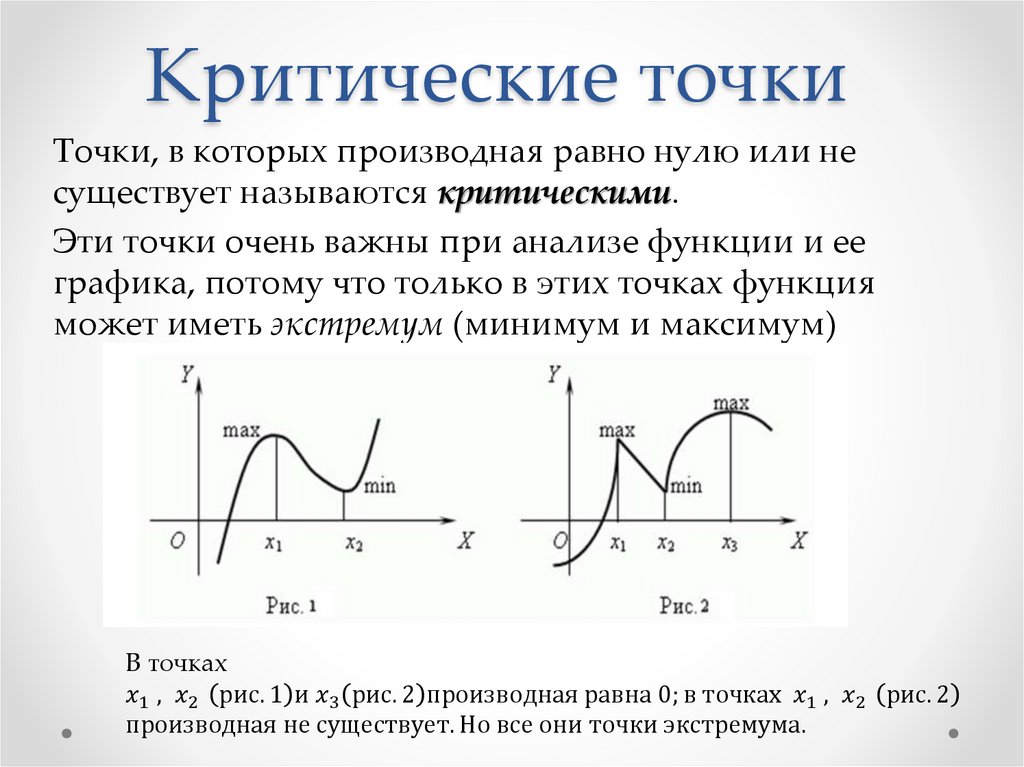
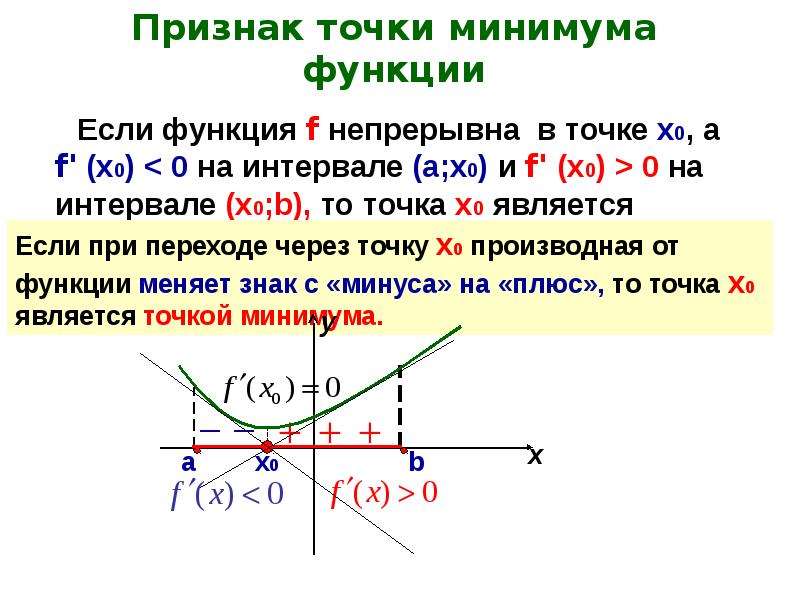
После нахождения всех потенциальных критических точек, исследуйте вторую производную функции, чтобы определить их природу (максимум, минимум или точка перегиба).
Читы к теме \
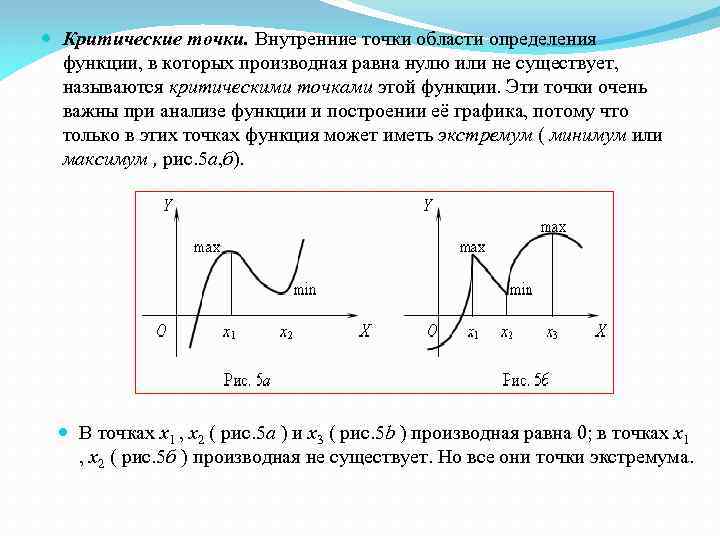
Для функций нескольких переменных используйте градиент вместо обычной производной для нахождения критических точек.
Необходимые и достаточные условия экстремума функции. 10 класс.
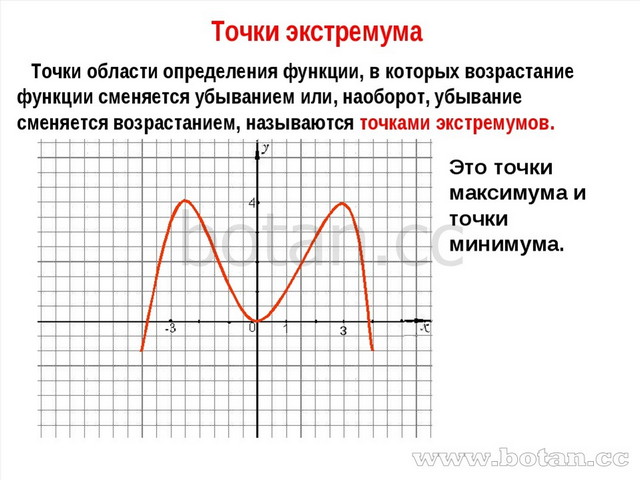
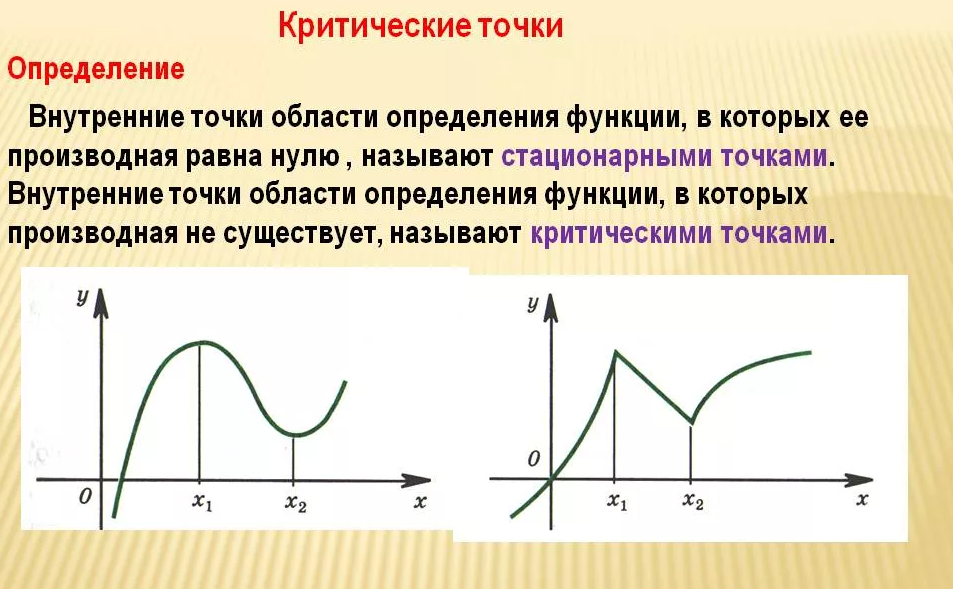
Помните, что не все точки, где производная равна нулю или не существует, обязательно являются локальными экстремумами. Проверьте значения функции в этих точках.

Если функция определена на ограниченном интервале, не забудьте проверить её значение на границах интервала.
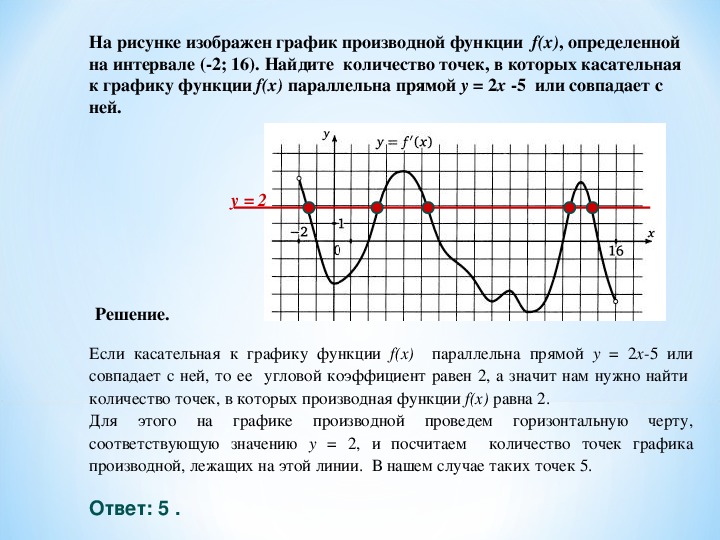
Используйте графики функции и её производной для наглядного представления критических точек и их свойств.
При анализе сложных функций могут понадобиться методы численного решения уравнений для нахождения критических точек.

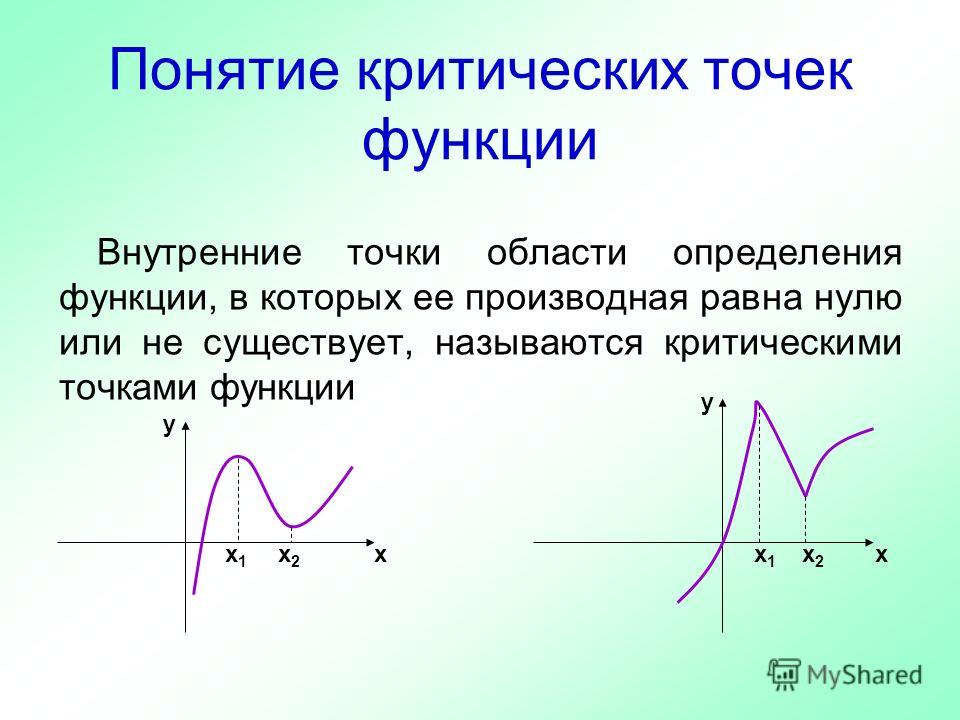
Не стесняйтесь обращаться к специализированной литературе и программному обеспечению для более глубокого анализа критических точек и их свойств.