Методы нахождения экстремумов по графику производной
Узнайте, как использовать график производной функции для определения количества и положения точек экстремума. Это поможет в анализе поведения функции и в решении задач по математике.
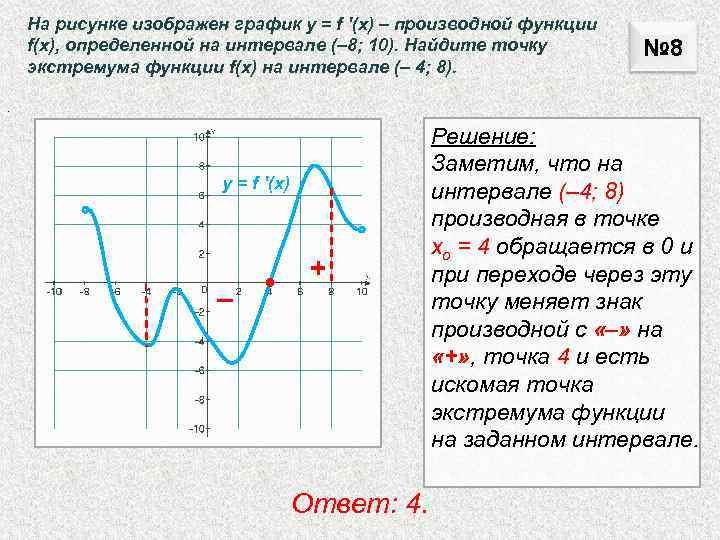
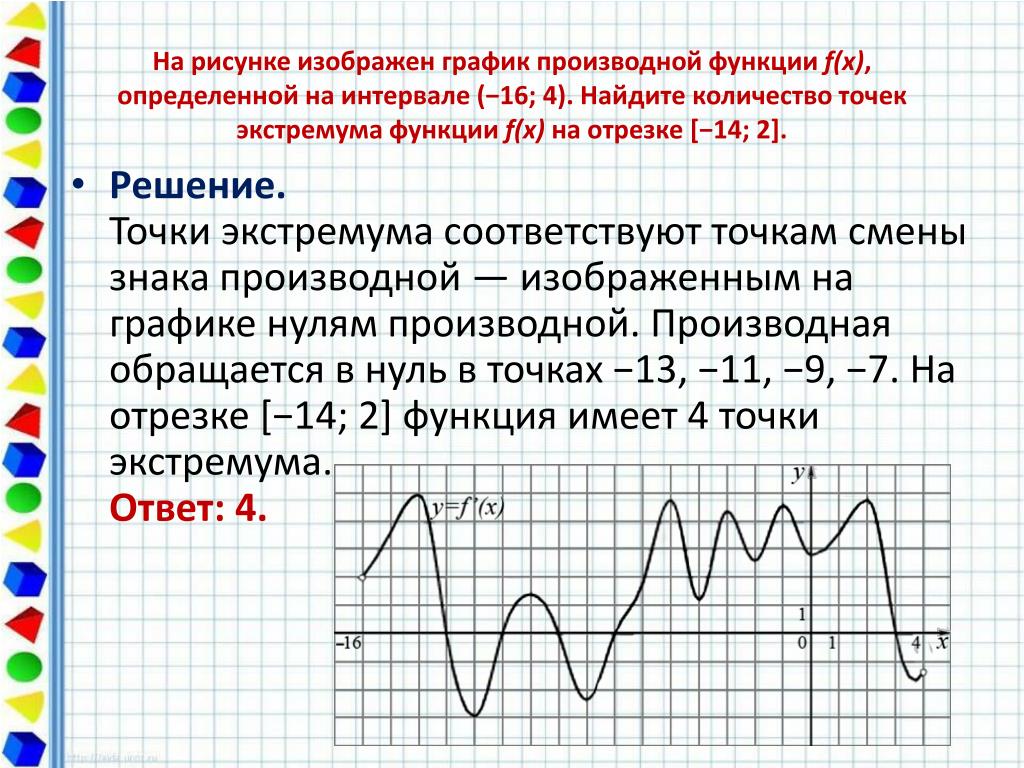
Внимательно изучите график производной, чтобы определить, где она пересекает ось абсцисс.
ЕГЭ 2022: Задание 6. Количество точек экстремума функции по производной
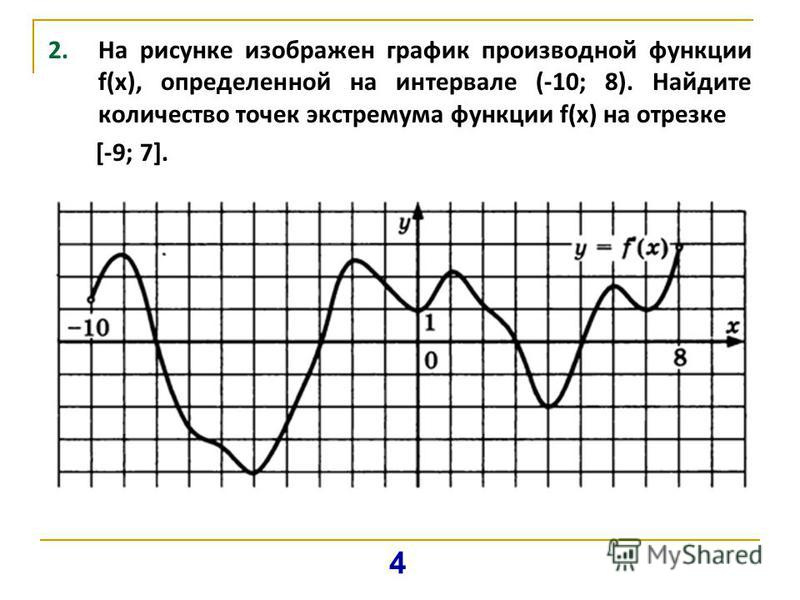
Экстремумы функции соответствуют нулям производной, поэтому важно находить такие точки.
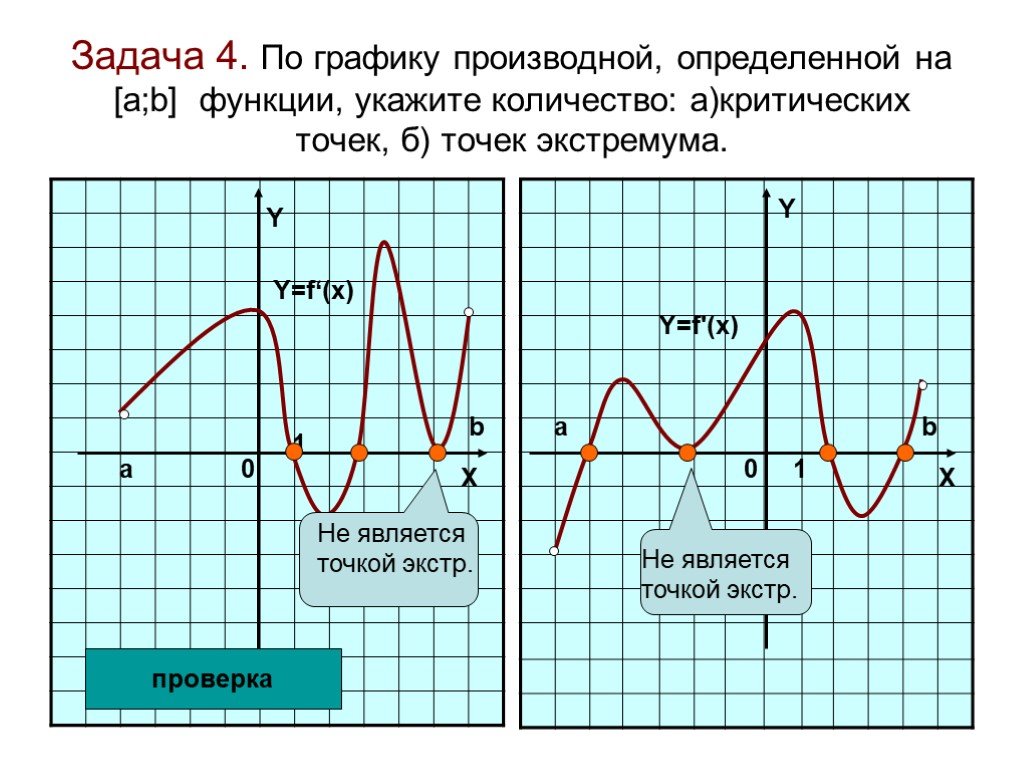

Проверьте, меняет ли производная знак в точках пересечения, это укажет на экстремум.
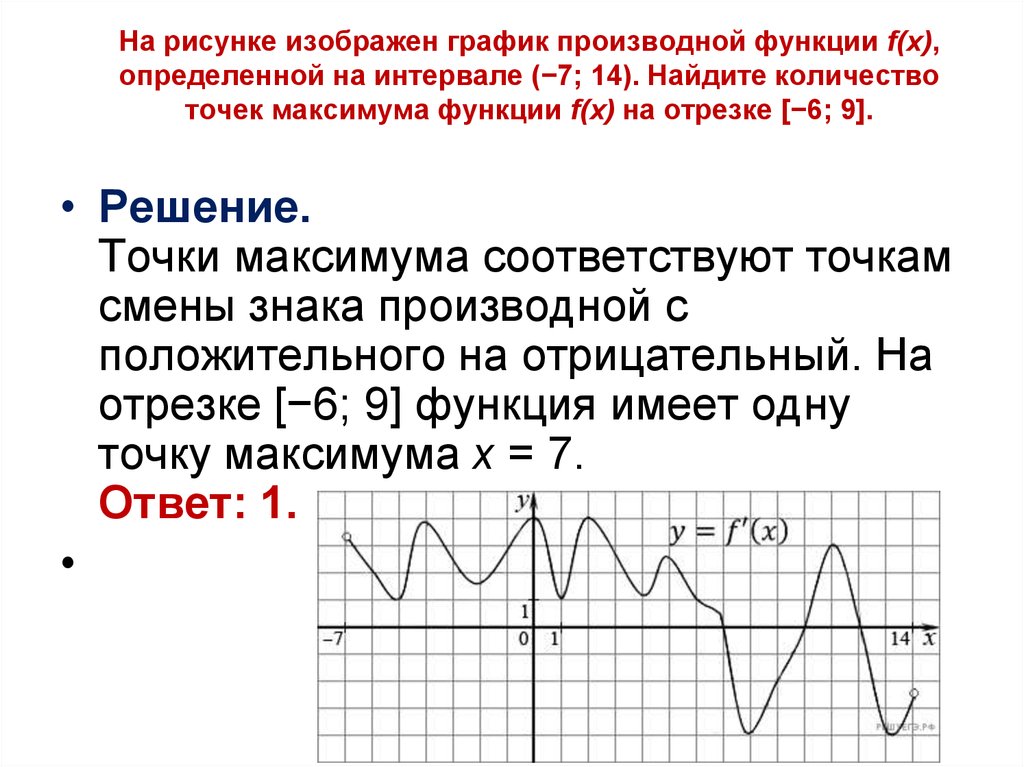
Используйте вторую производную, чтобы определить характер экстремума: максимум или минимум.
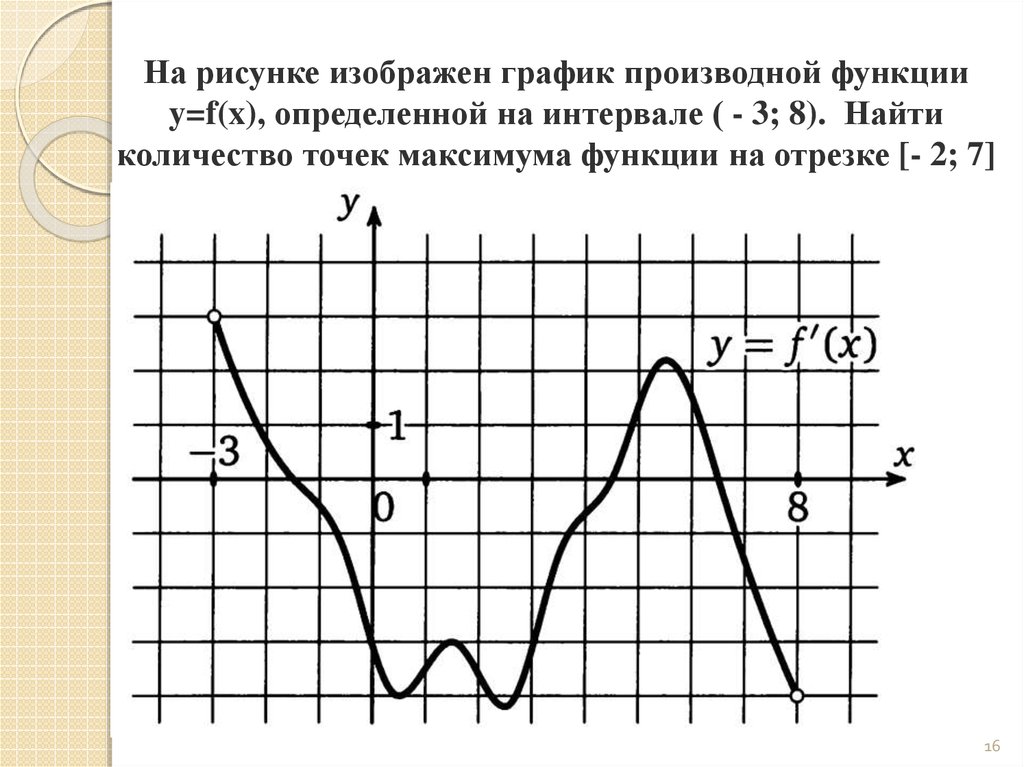
По графику производной найти количество точек максимума функции
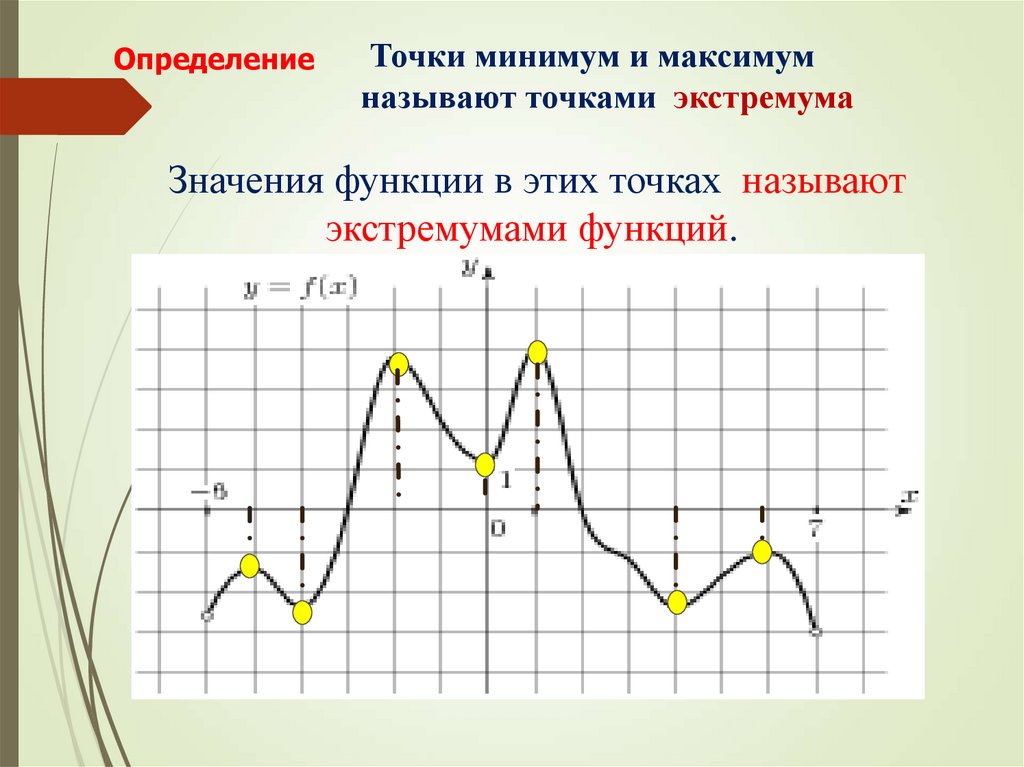
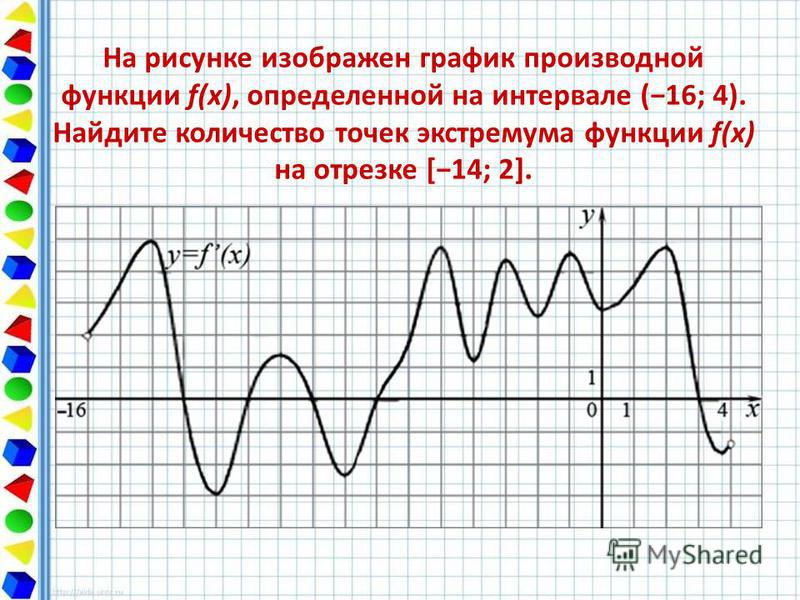
Если вторая производная положительна, это минимум, если отрицательна — максимум.
Точки ЭКСТРЕМУМА на графике производной / разбор ЕГЭ #27496
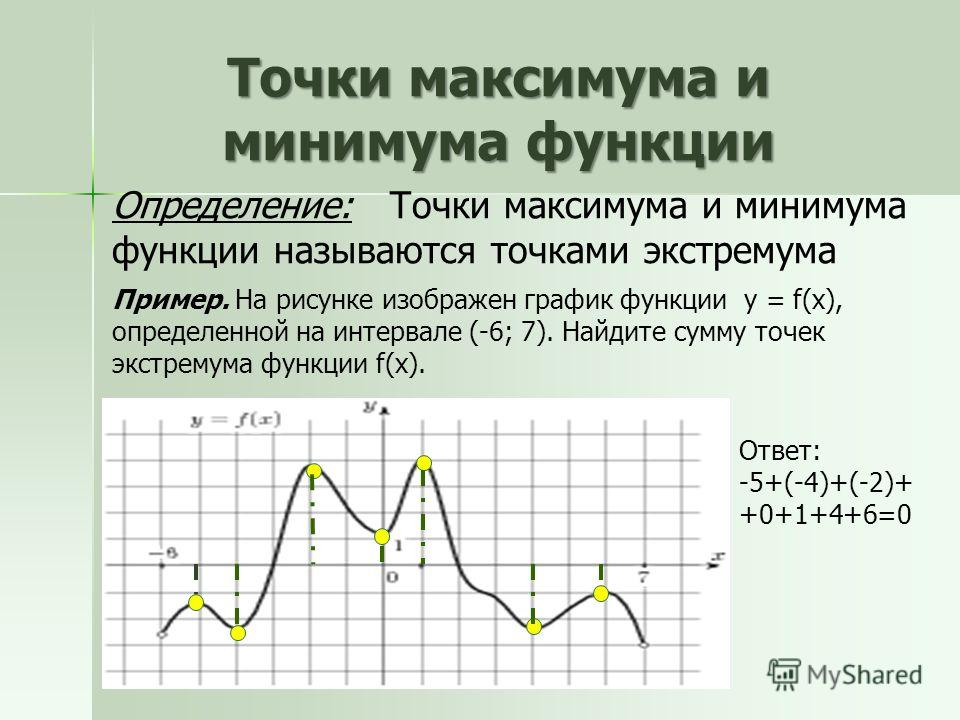
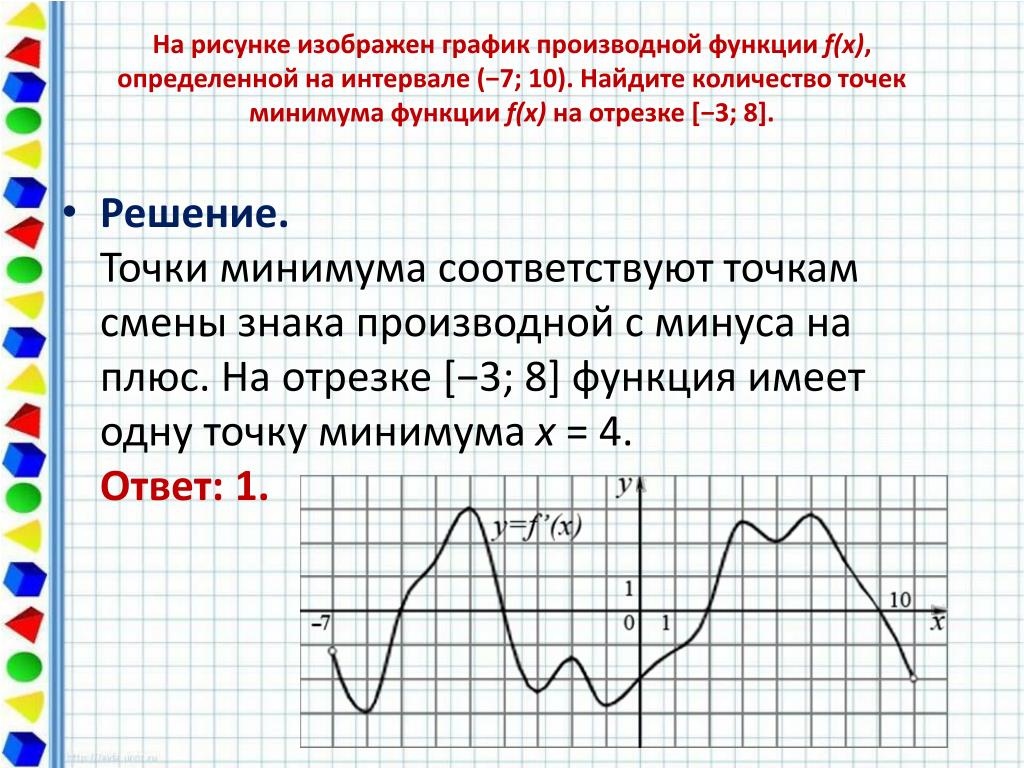
Промежутки постоянного знака первой производной указывают на монотонность функции.
Постройте таблицу знаков для лучшего понимания изменения функции.
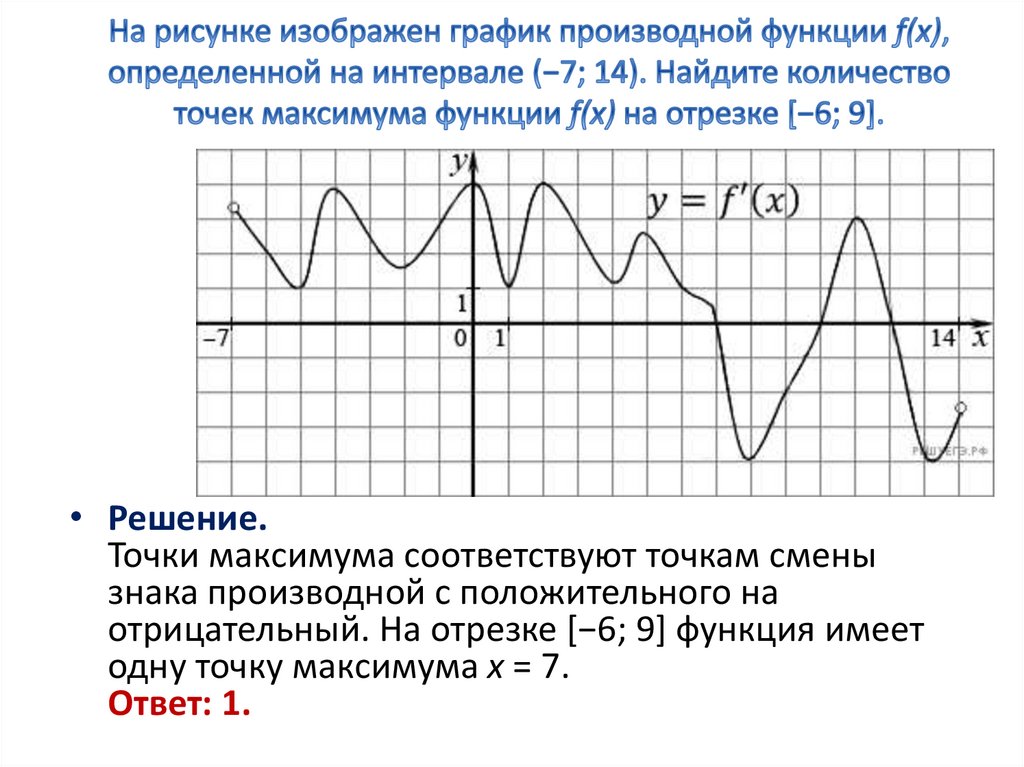
Используйте графические приложения для более точного анализа поведения функции.
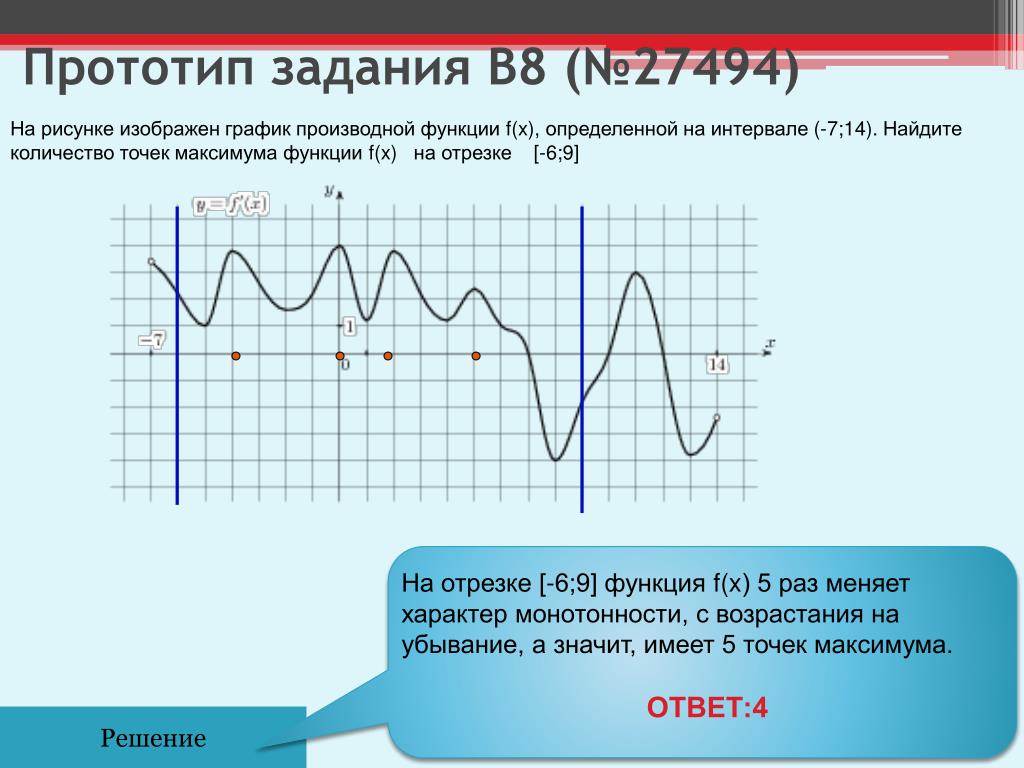
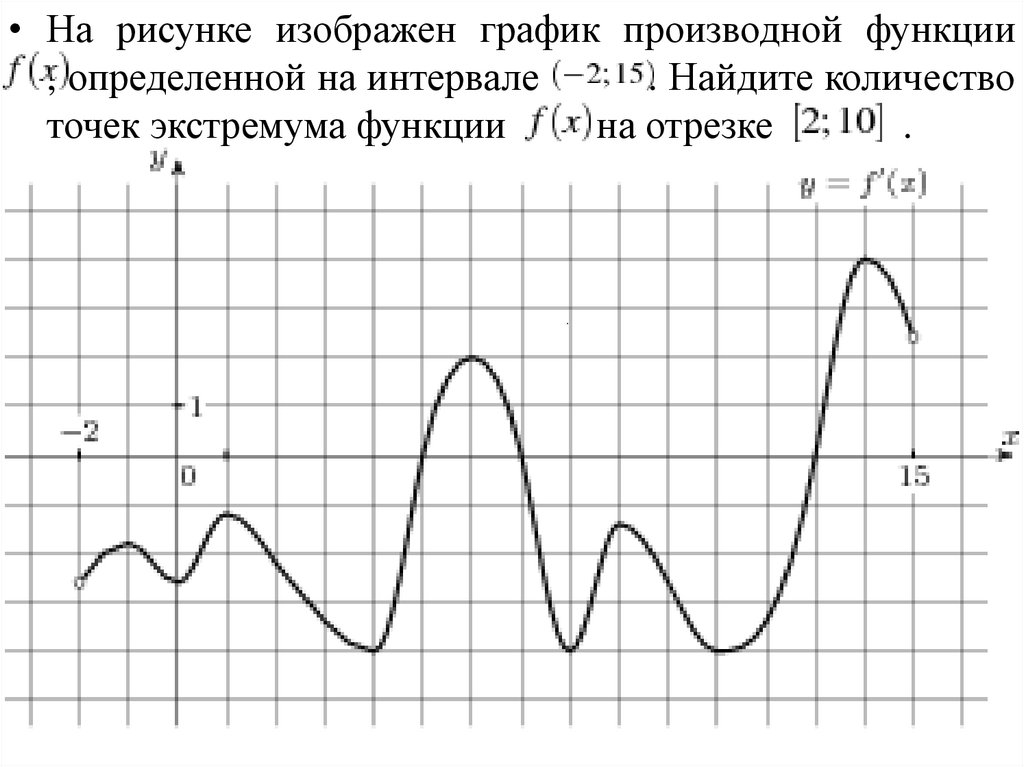
Помните, что отсутствие нулей у производной не исключает существование экстремумов.
Производная в ЕГЭ. Точки экстремума на графике производной
Экспериментируйте с различными примерами для лучшего понимания теоретического материала.