Графическое представление комплексных чисел в координатной системе
Комплексные числа могут быть визуализированы на координатной плоскости, что помогает лучше понять их свойства и операции с ними. На этой странице вы найдете фотографии и полезные советы по работе с комплексными числами в системе координат.

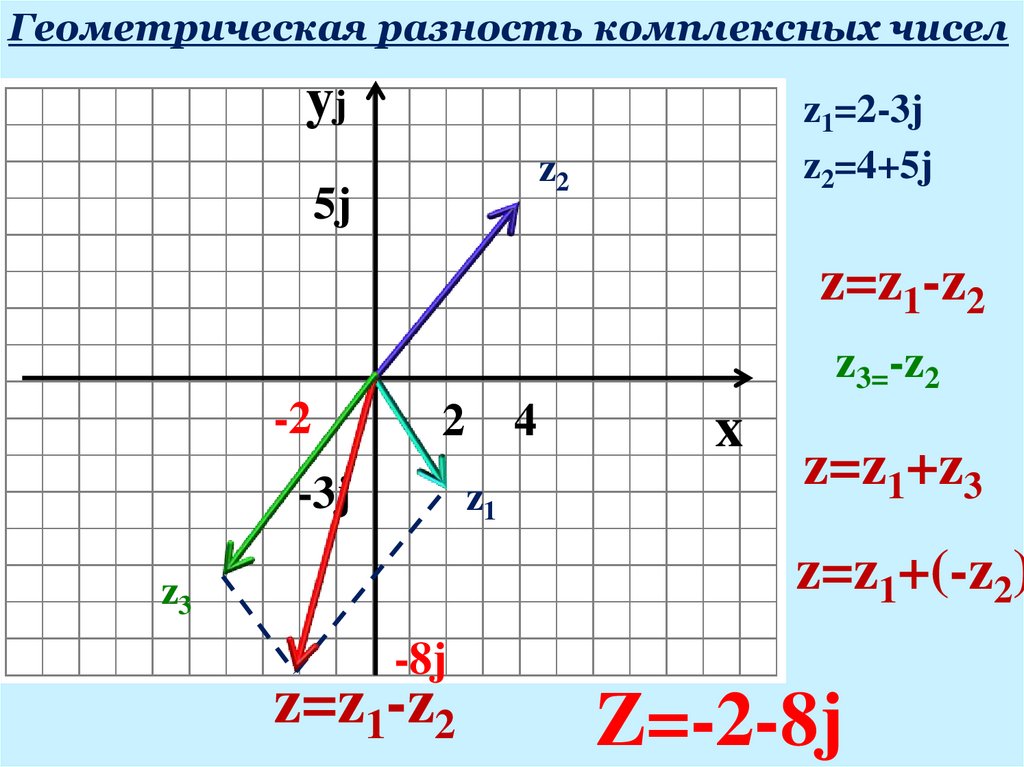
Для наглядного представления комплексного числа используйте декартову координатную систему, где действительная часть откладывается по оси x, а мнимая часть по оси y.

Для обозначения комплексного числа на координатной плоскости используйте точку или стрелку, исходящую из начала координат.
Тригонометрическая форма комплексного числа
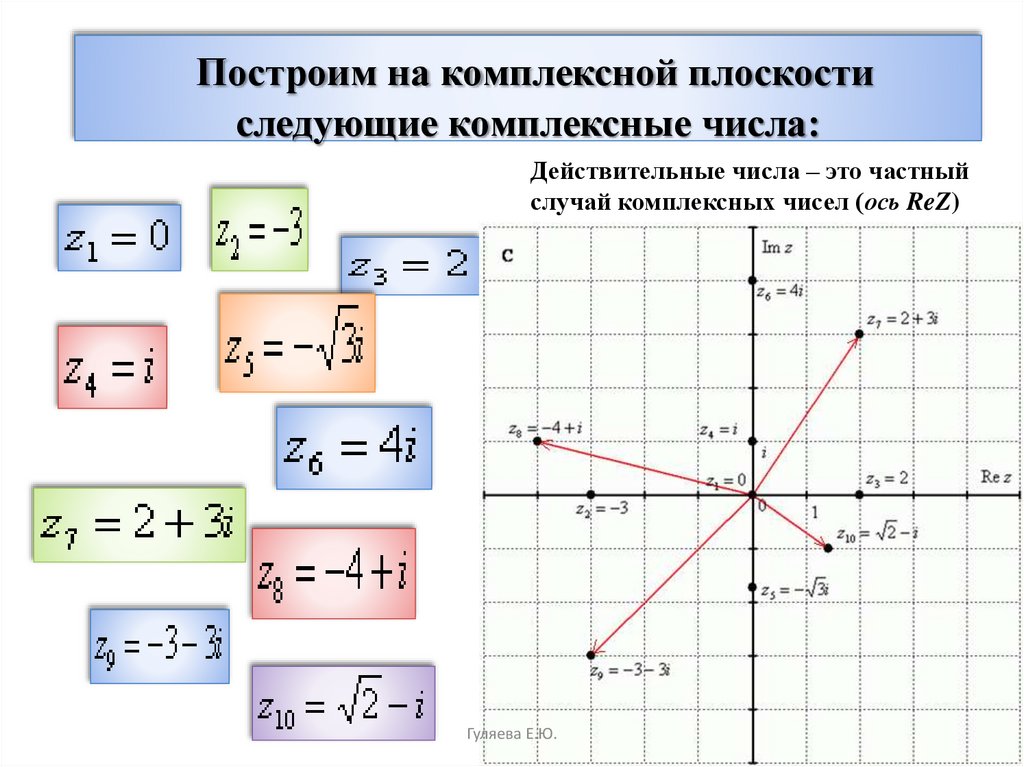
Чтобы лучше понять аргумент комплексного числа, постройте угол между положительным направлением оси x и отрезком, соединяющим начало координат с точкой на плоскости.

Помните, что модуль комплексного числа равен длине отрезка от начала координат до точки на плоскости и вычисляется по теореме Пифагора.
М10 (33.1-33.12). Комплексные числа и координатная плоскость. ReZ ImZ.

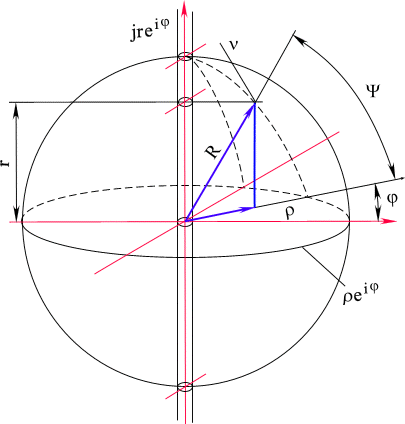
Используйте полярную форму записи комплексных чисел для упрощения умножения и деления, представив число как произведение его модуля и экспоненты от аргумента.
Изобразить область на комплексной плоскости

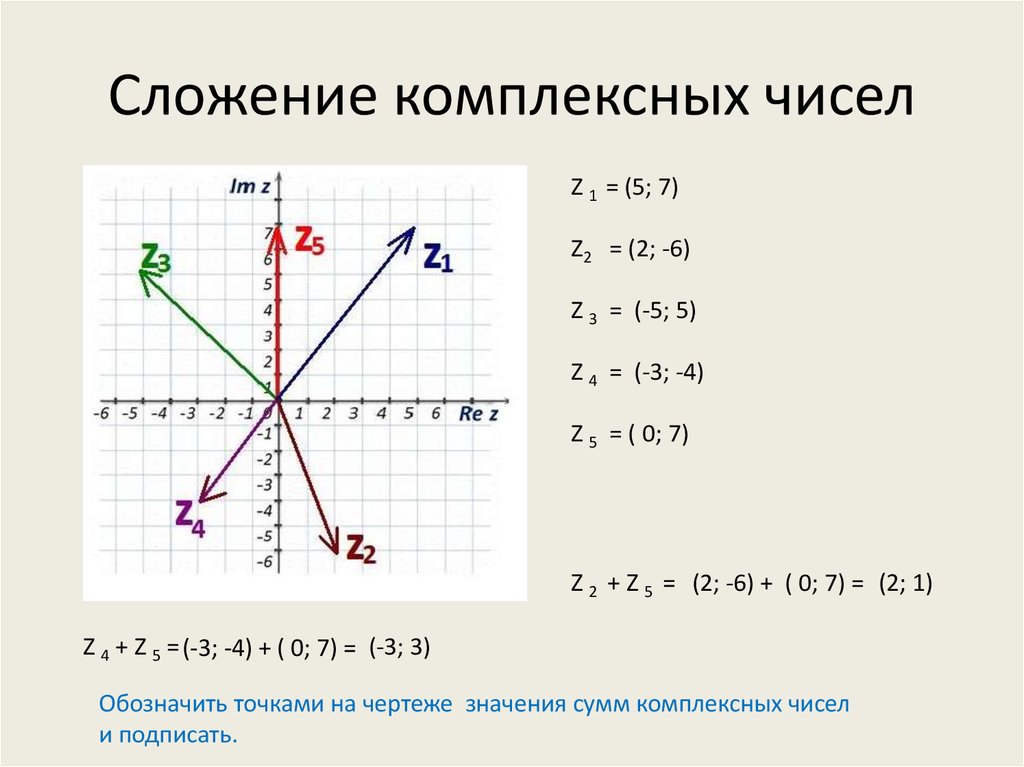
Для сложения и вычитания комплексных чисел просто складывайте или вычитайте их действительные и мнимые части соответственно.

Чтобы умножить два комплексных числа, умножьте их модули и сложите их аргументы.

Для деления комплексных чисел разделите их модули и вычтите аргументы.
Для визуализации сопряженного комплексного числа отразите его по оси x.
Комплексные числа и их операции часто используются в электротехнике, квантовой механике и других областях науки и техники.