Выявление косинуса угла между плоскостями: практическое руководство

Эта страница содержит полезные советы и пошаговые инструкции по вычислению косинуса угла между двумя плоскостями, что может быть полезно для студентов, инженеров и всех, кто интересуется математикой и геометрией.

Начните с определения нормалей каждой из плоскостей. Нормали — это векторы, перпендикулярные плоскости.

Векторы нормалей можно найти, используя коэффициенты уравнений плоскостей.

Обозначьте нормали как векторы N1 и N2.

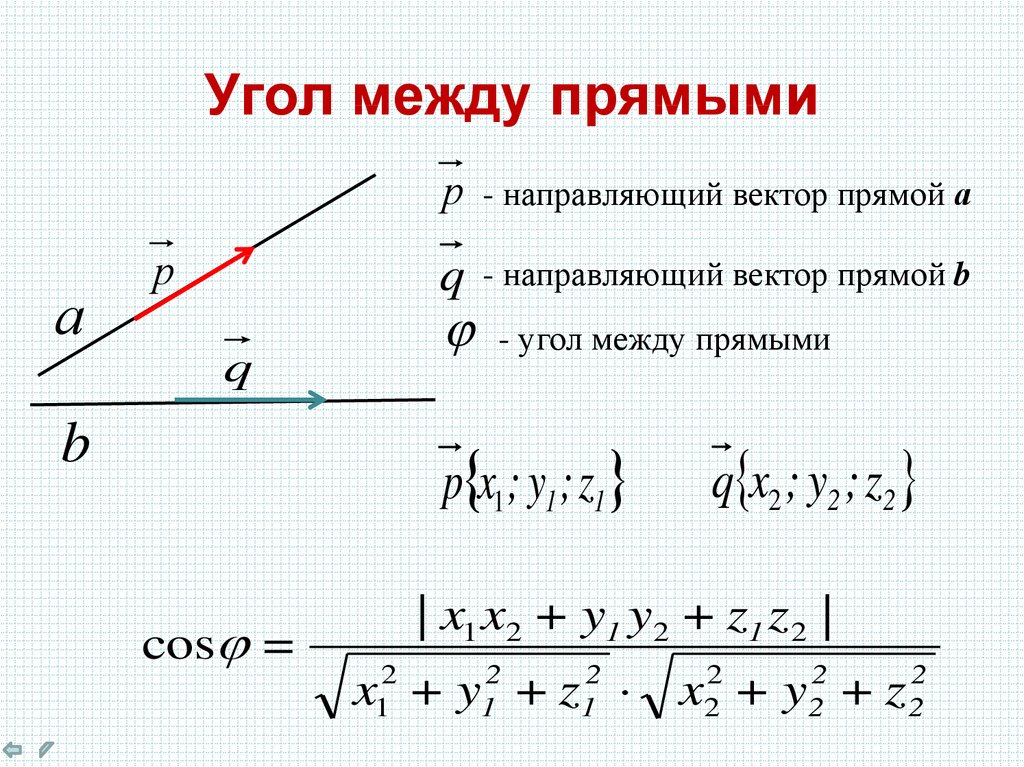
Для нахождения косинуса угла между нормалями используйте скалярное произведение векторов.

Скалярное произведение векторов можно найти по формуле: N1•N2 = |N1| * |N2| * cos(θ).

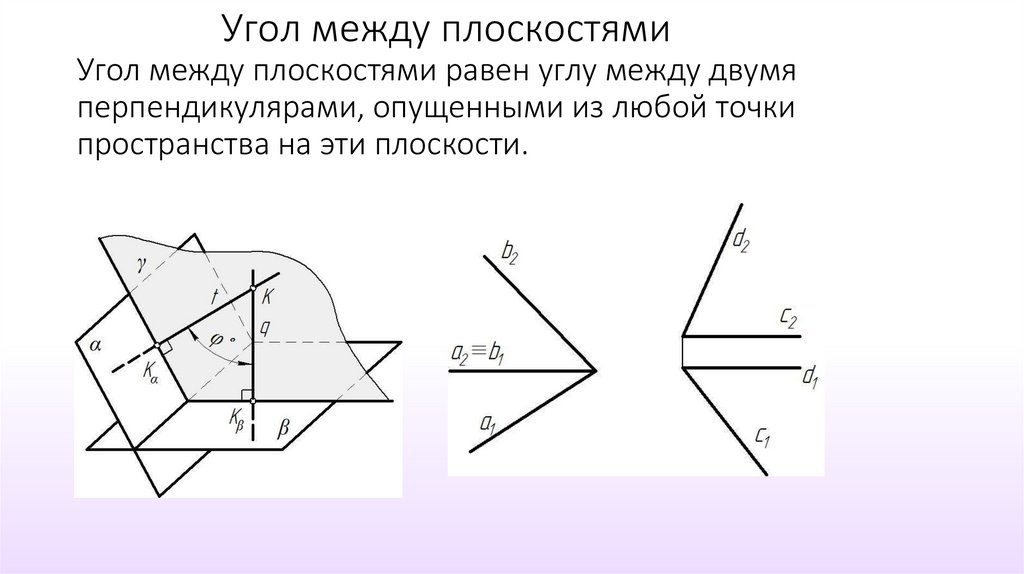
Из этой формулы выразите косинус угла: cos(θ) = (N1•N2) / (|N1| * |N2|).

Не забудьте вычислить модули векторов N1 и N2.

Для этого используйте формулу модуля вектора: |N| = √(N_x² + N_y² + N_z²).

Проверьте все вычисления, чтобы избежать ошибок.

Используйте калькулятор для точного расчета значений скалярного произведения и модулей векторов.