Изучаем квадратную функцию y = x²: шаг за шагом

Квадратная функция y = x² является одной из основных функций в алгебре и математическом анализе. На этой странице вы найдете полезные советы и примеры для понимания и построения графика этой функции.

Начните с определения квадратичной функции: y = x², где y - это квадрат x.

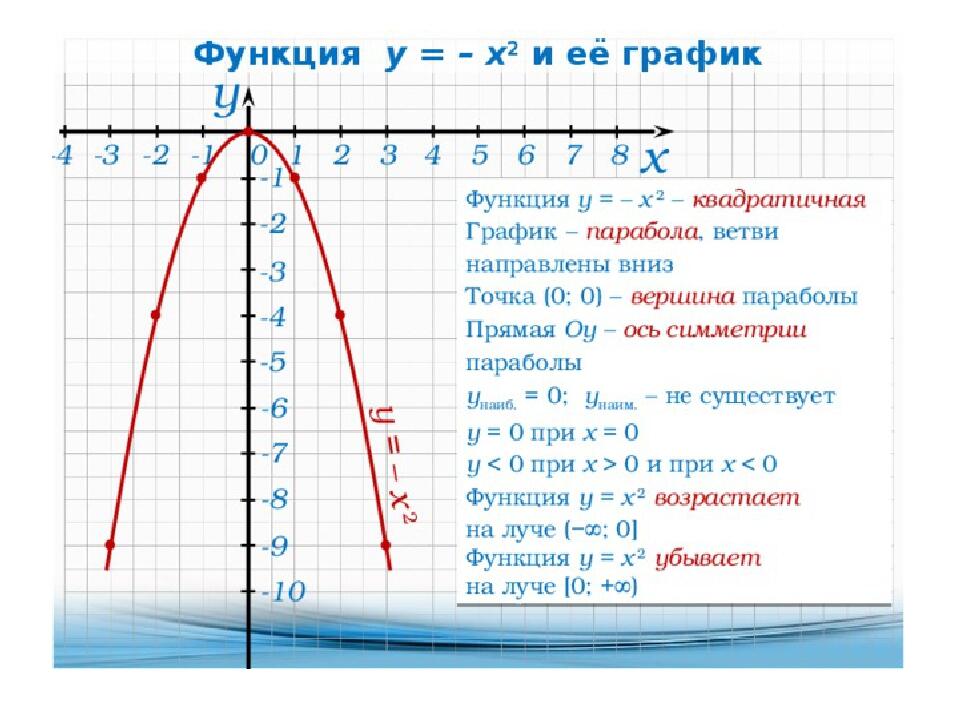
Обратите внимание на вершину параболы: для функции y = x² вершина находится в точке (0,0).

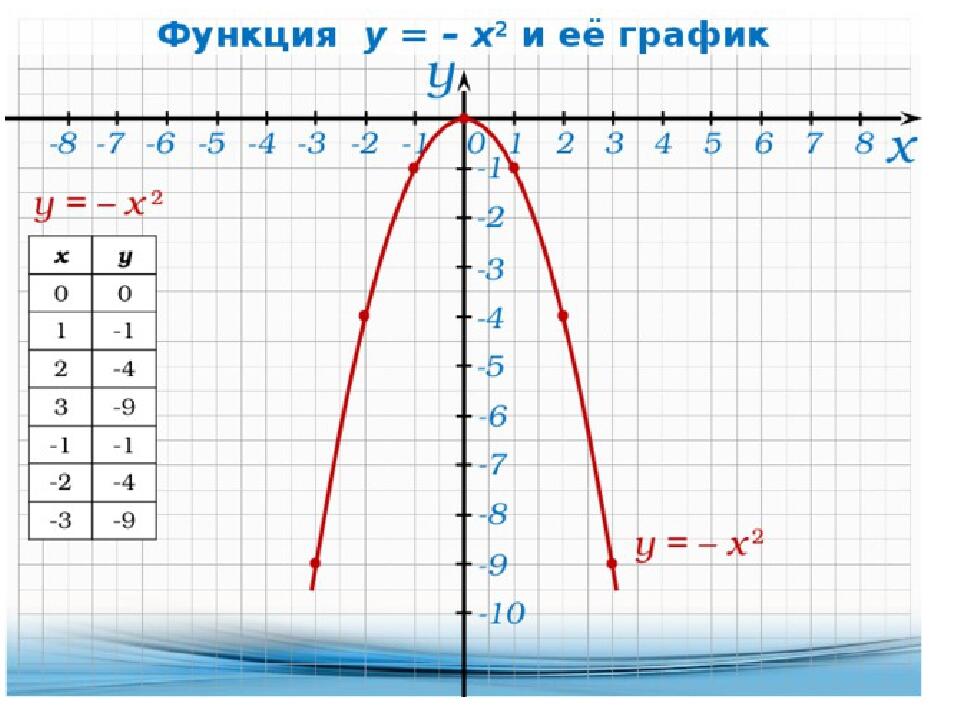
Исследуйте симметрию графика: он симметричен относительно оси y.

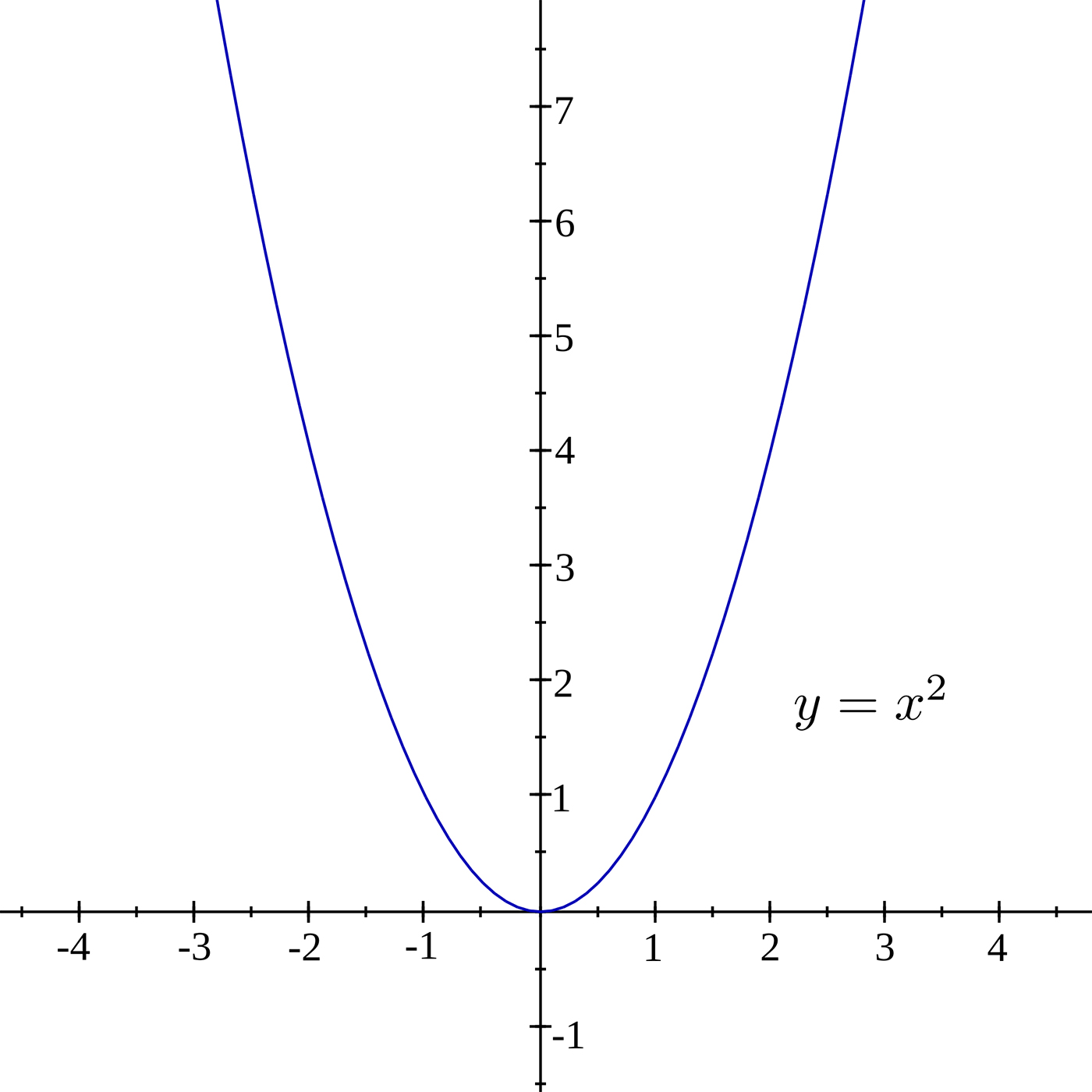
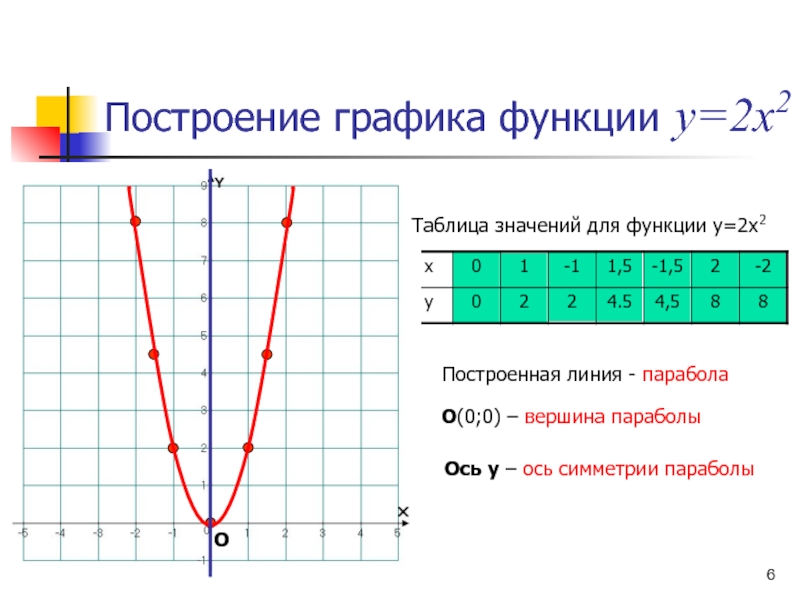
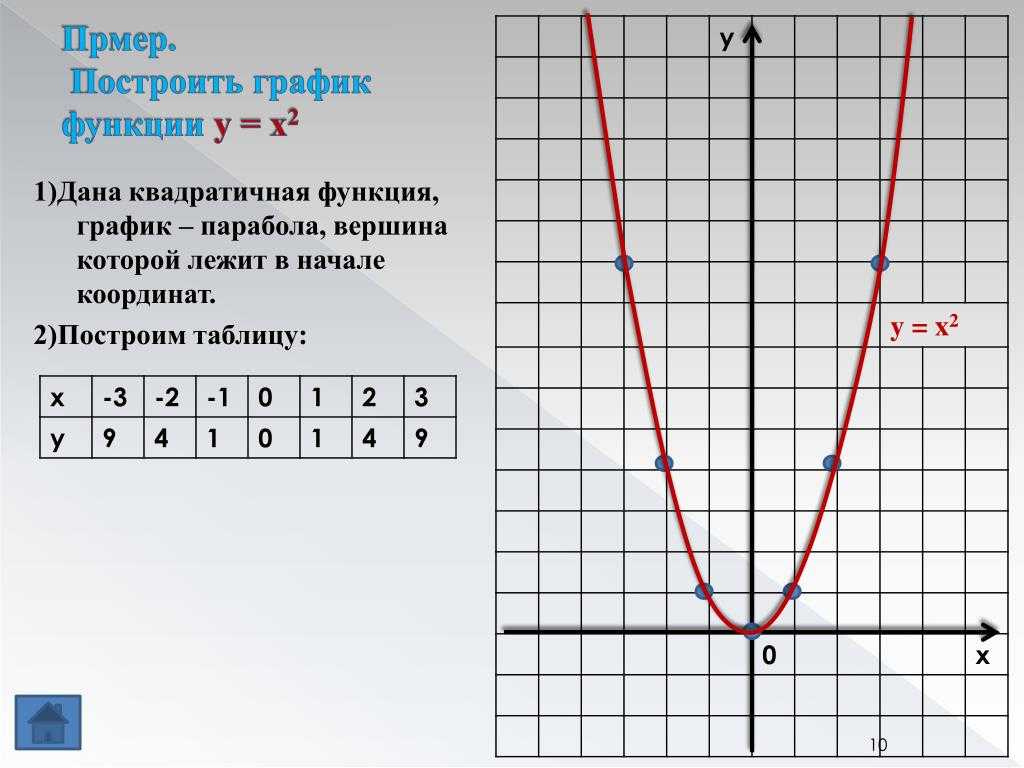
Используйте таблицу значений для построения графика: выберите несколько значений x и вычислите соответствующие значения y.

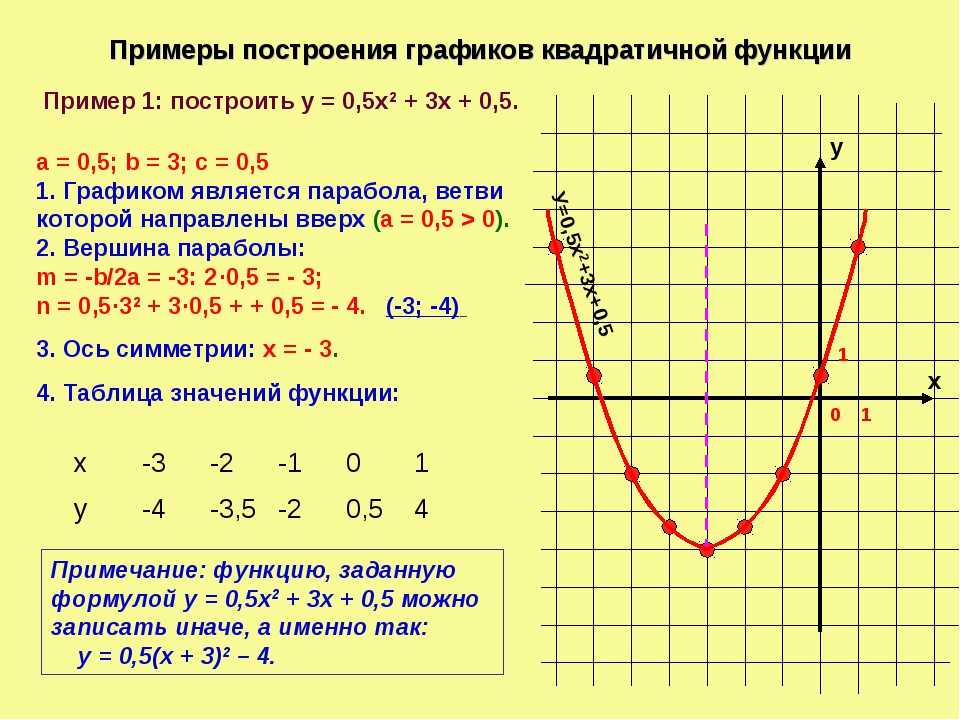
Постройте оси координат и отметьте точку (0,0), которая является вершиной параболы.

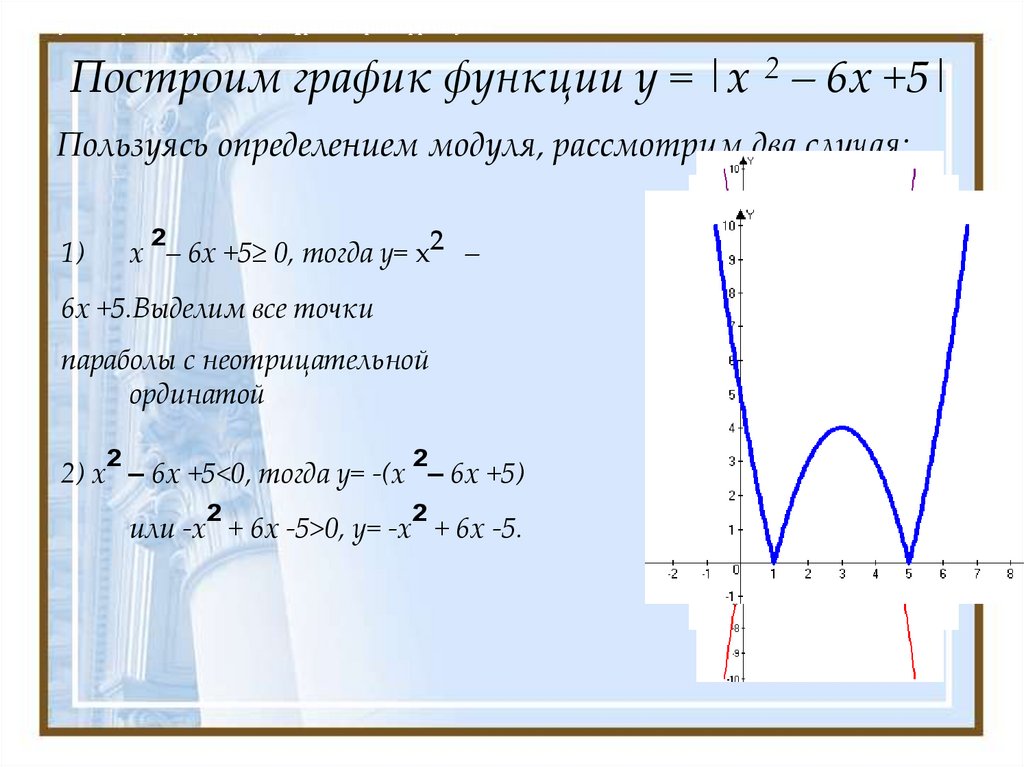
Нанесите на график точки, вычисленные в таблице значений, и соедините их плавной кривой.

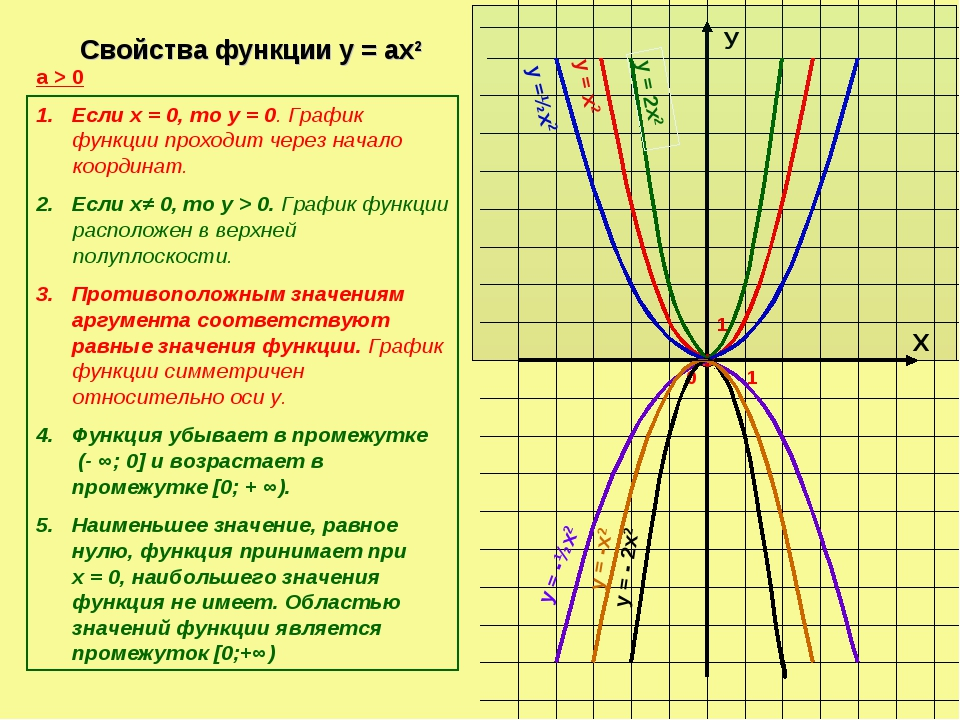
Помните, что график функции y = x² всегда направлен вверх, так как коэффициент перед x² положительный.

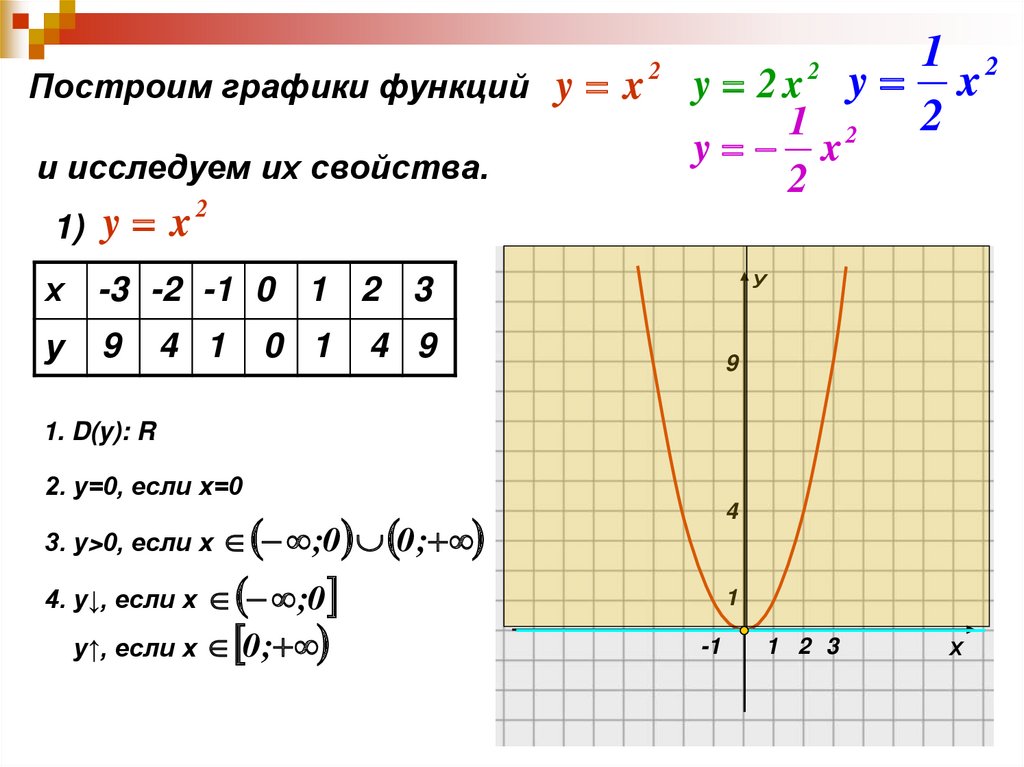
Изучите свойства параболы: она возрастает на интервале (0, ∞) и убывает на интервале (-∞, 0).

Используйте графический калькулятор для проверки точности вашего графика.

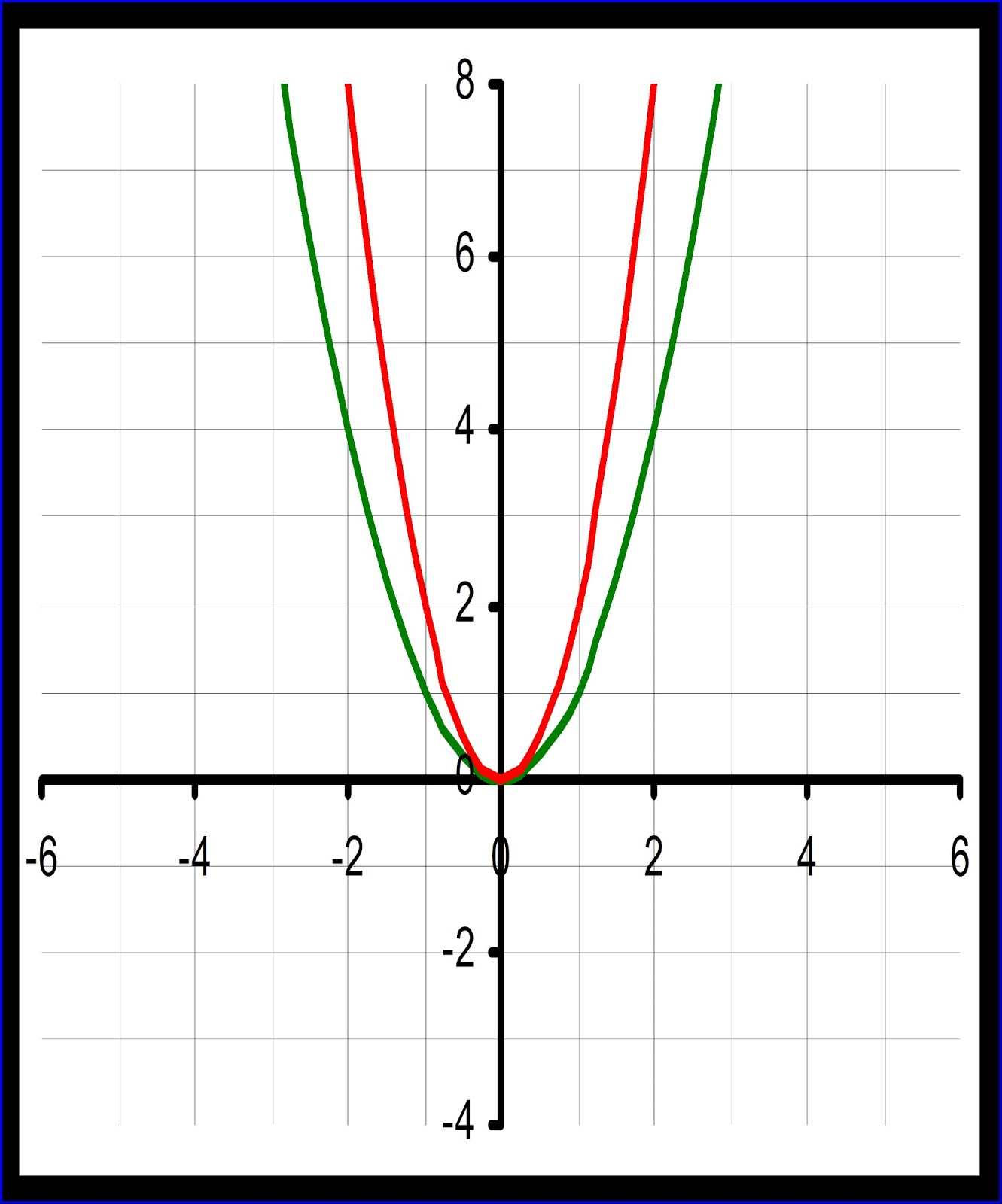
Понимание основ квадратной функции поможет вам в изучении более сложных математических понятий и функций.