Как правильно анализировать графики дифференцируемых функций
На этой странице вы найдете подборку фотографий и полезные советы по анализу и интерпретации графиков дифференцируемых функций, что поможет вам лучше понять эту важную математическую тему.
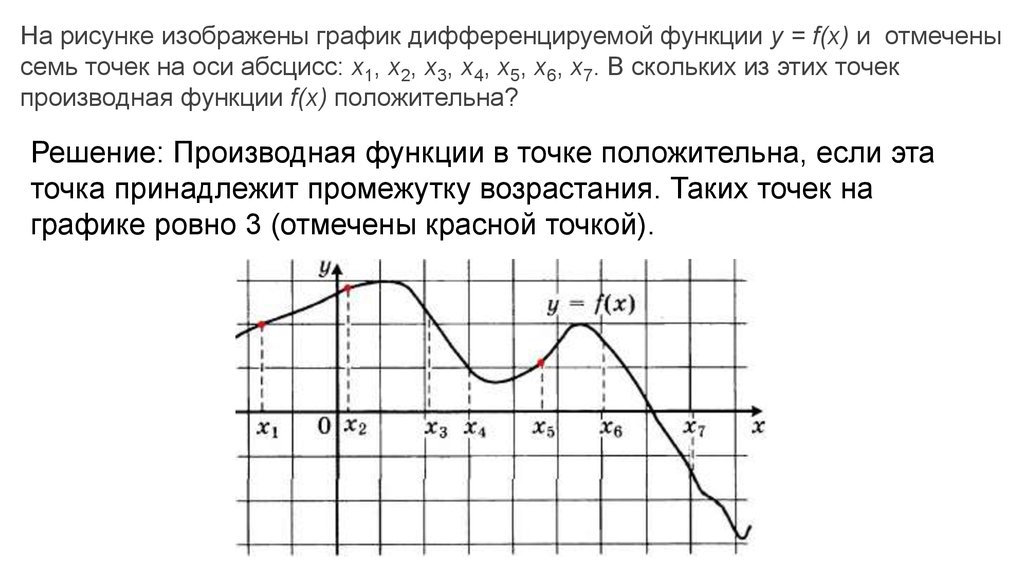


Изучите основные свойства дифференцируемых функций, такие как непрерывность и гладкость графика.

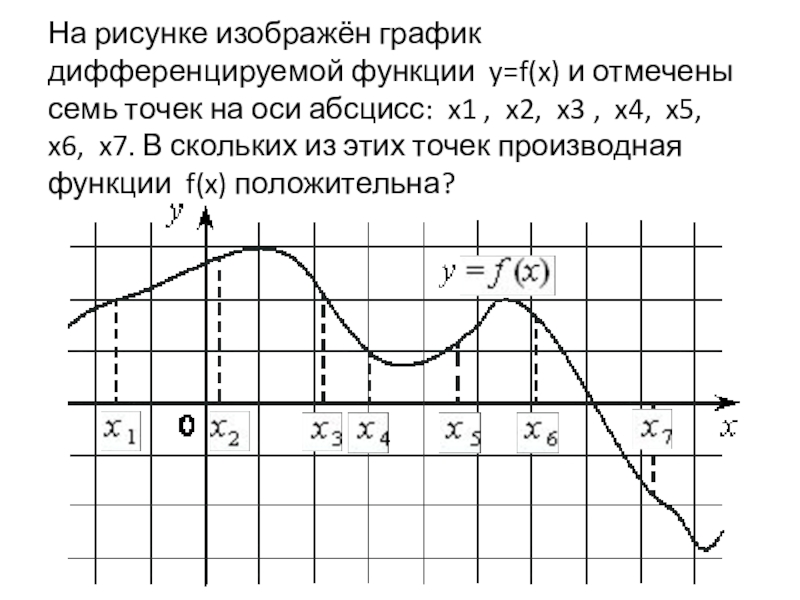
Определите критические точки функции, где её производная равна нулю или не существует.
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите
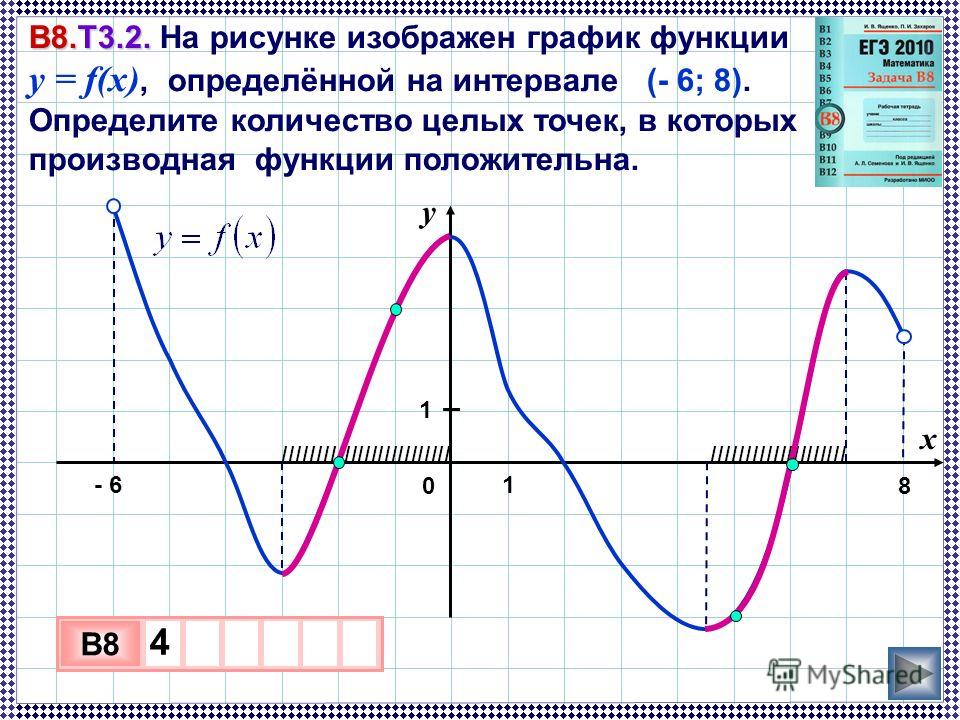
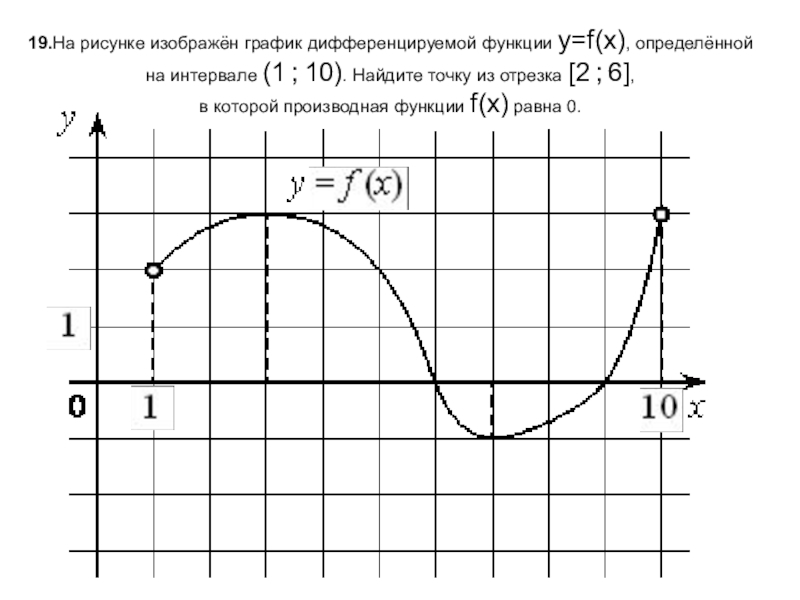
Анализируйте поведение функции на интервалах между критическими точками для понимания её роста или убывания.
На рисунке изображен график функции f(x)=acosx+b. Найдите а. (профильный ЕГЭ, задача 11)
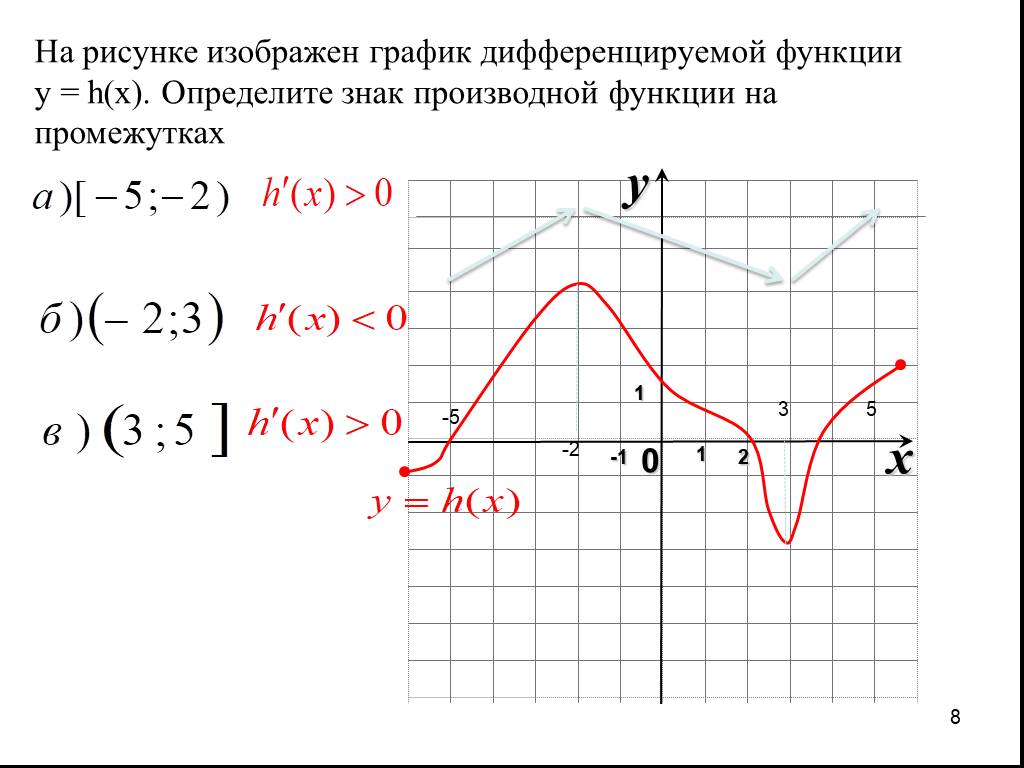
Используйте вторую производную для определения вогнутости или выпуклости графика функции.
Научитесь находить точки перегиба, где функция меняет свою вогнутость или выпуклость.
На рисунке изображен график функции. Найдите количество точек в которых производная функции равна 0.
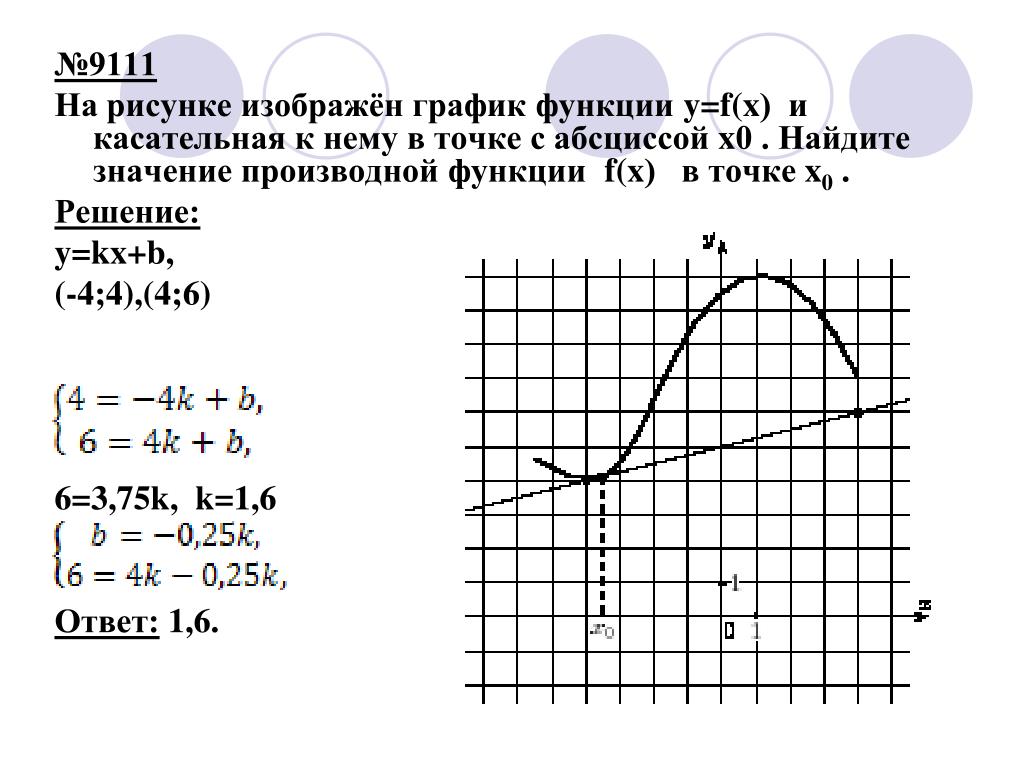
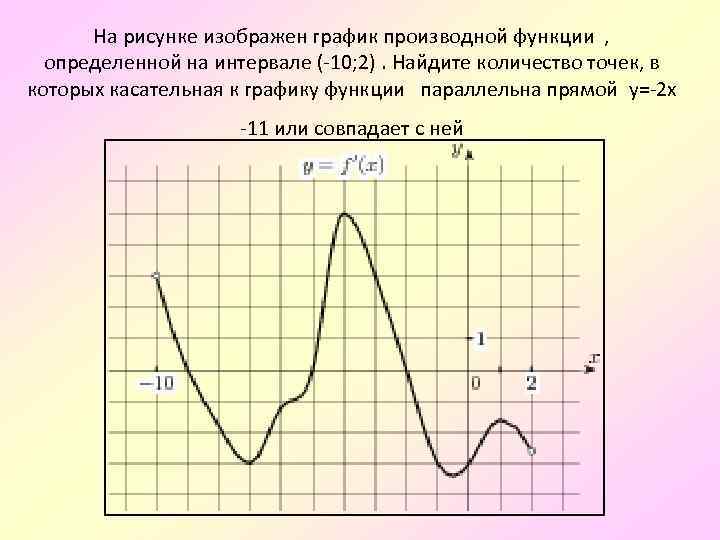
Практикуйтесь в построении графиков дифференцируемых функций вручную, чтобы лучше понять их поведение.
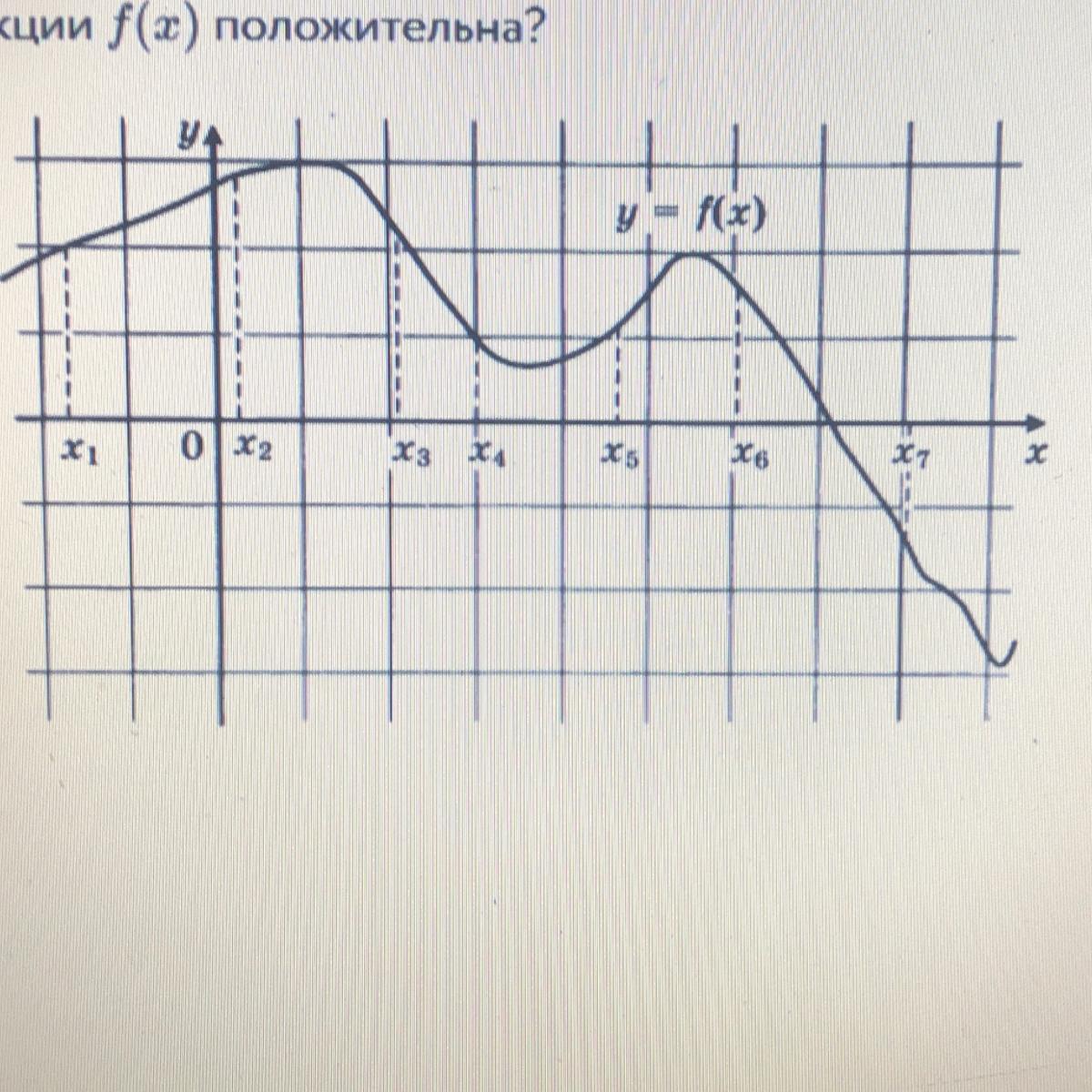

Используйте графические калькуляторы или компьютерные программы для проверки своих построений.
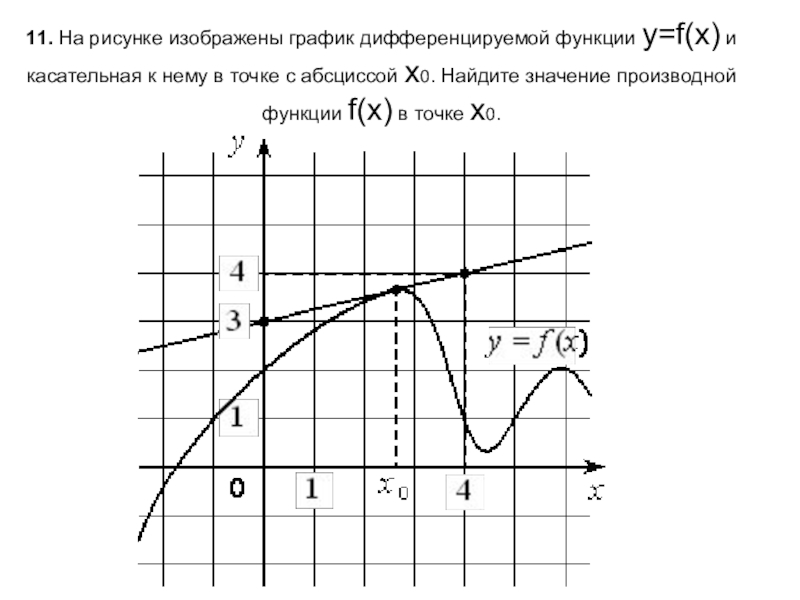
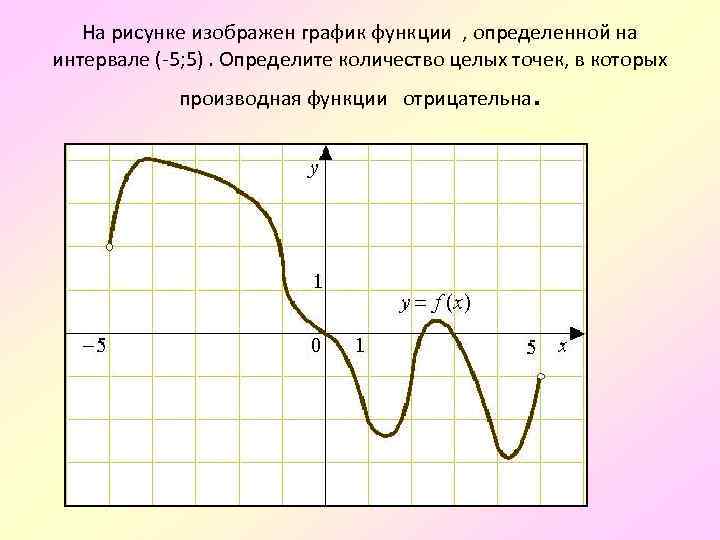
Изучайте примеры графиков различных дифференцируемых функций и их особенности.
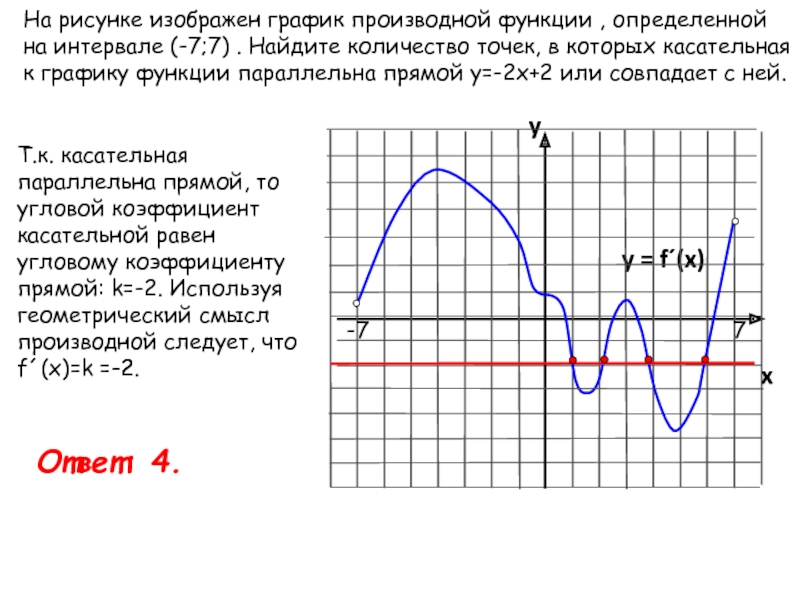
Практикуйтесь в решении задач на нахождение производных и их применение к анализу графиков.
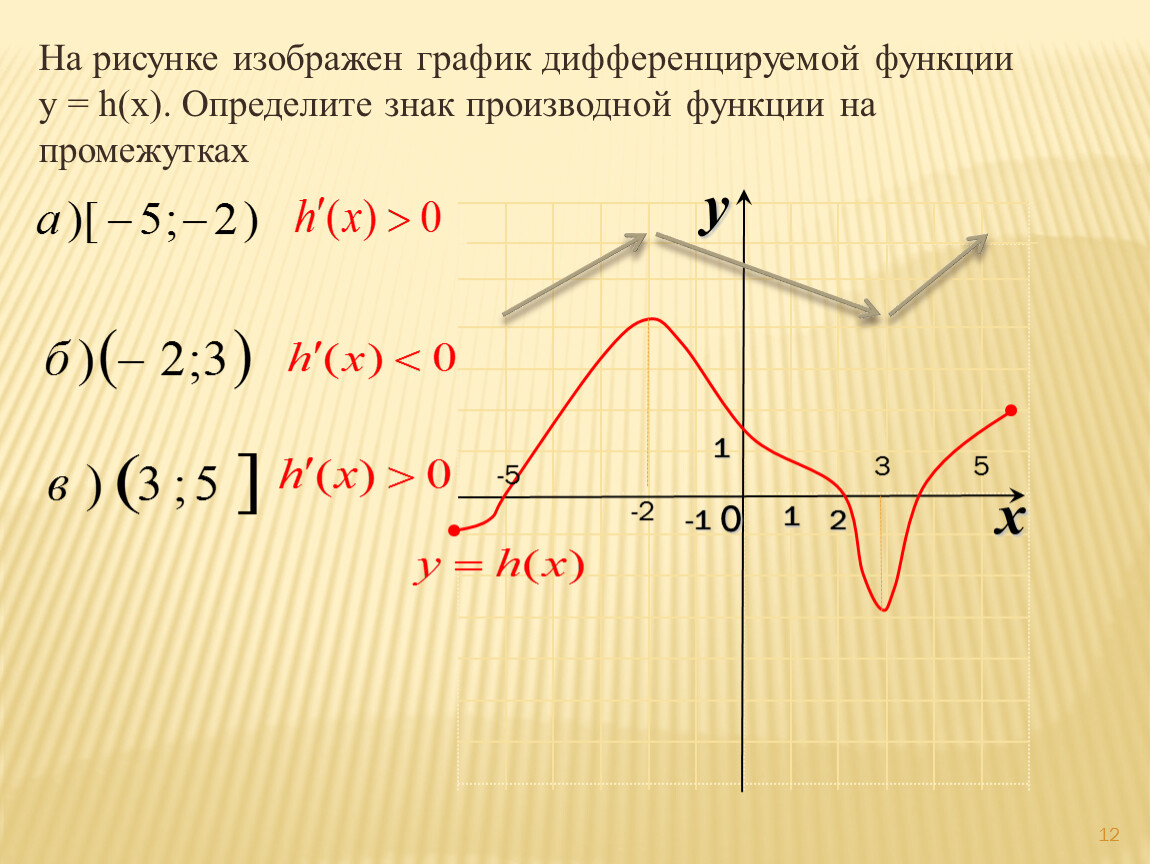

Не забывайте о контексте задачи: интерпретируйте результаты анализа графиков в соответствии с реальной ситуацией.