Эффективные методы нахождения углов в прямоугольном треугольнике

На этой странице вы найдете полезные советы и фотографии, которые помогут вам разобраться в методах нахождения углов в прямоугольном треугольнике. Узнайте, как применять тригонометрические функции и теорему Пифагора для решения задач по геометрии.

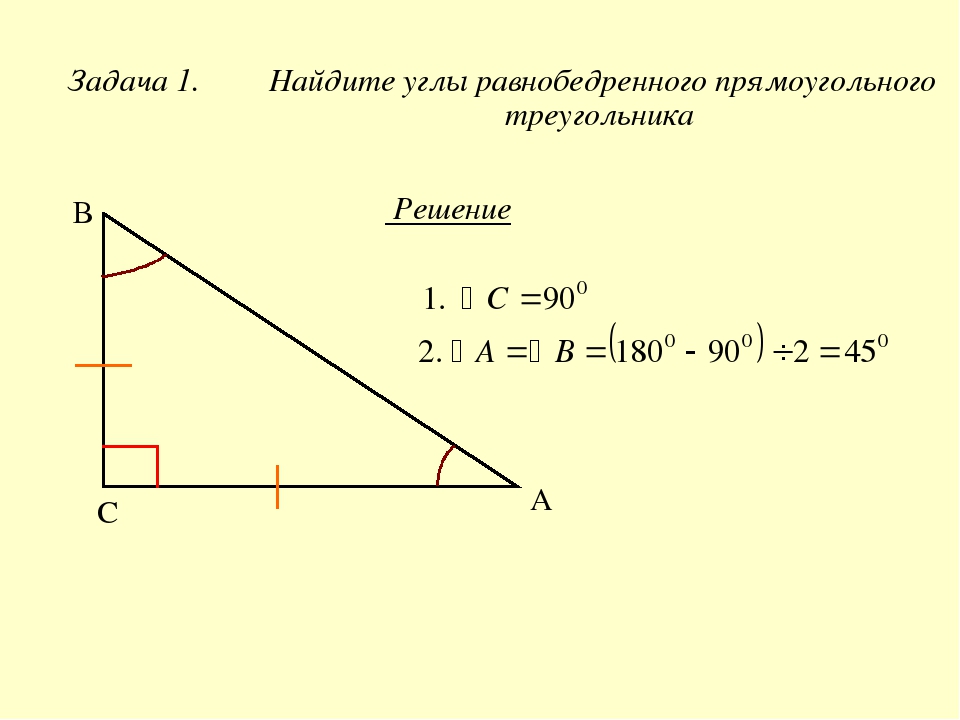
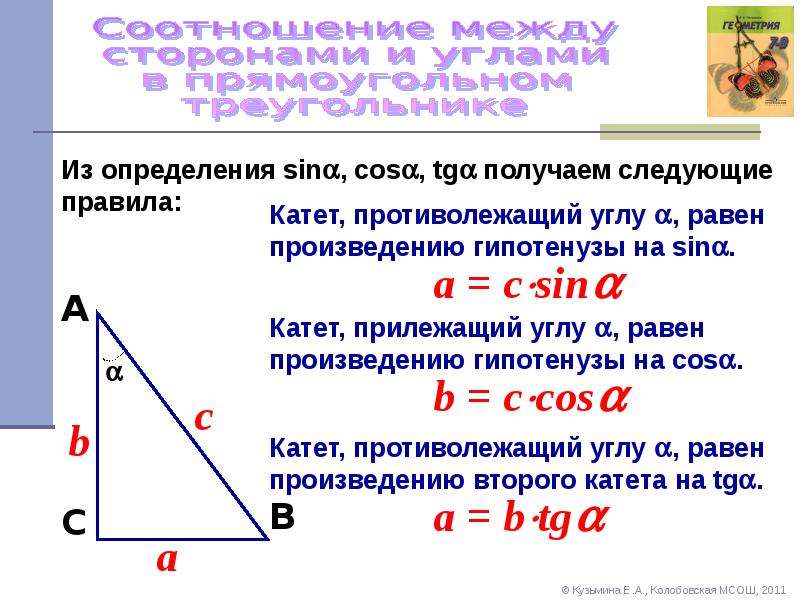
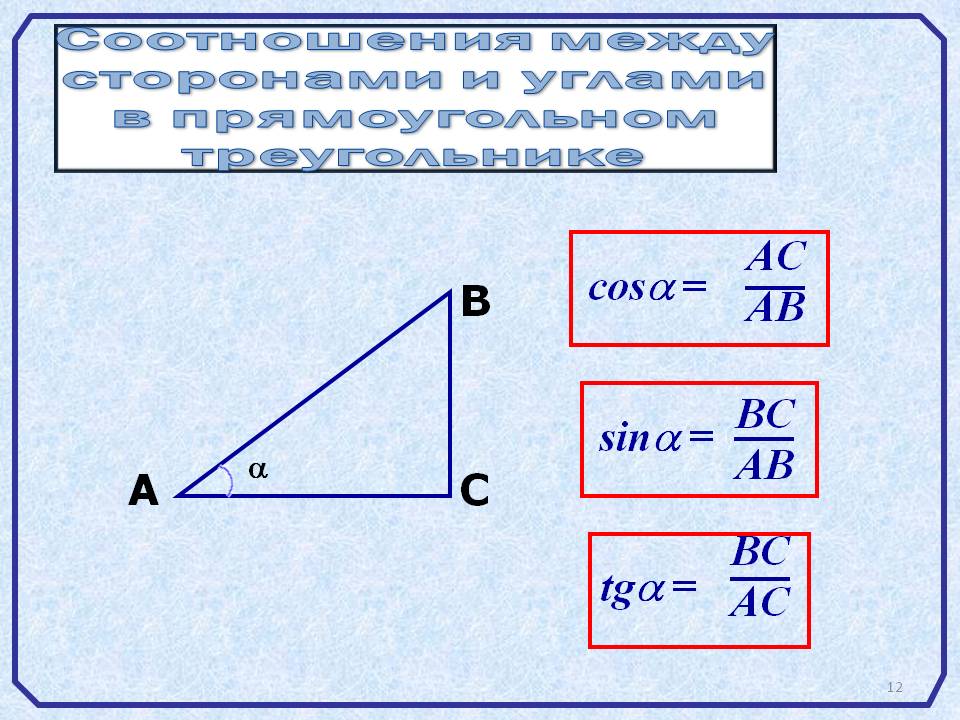
Для нахождения углов в прямоугольном треугольнике используйте тригонометрические функции: синус, косинус и тангенс.

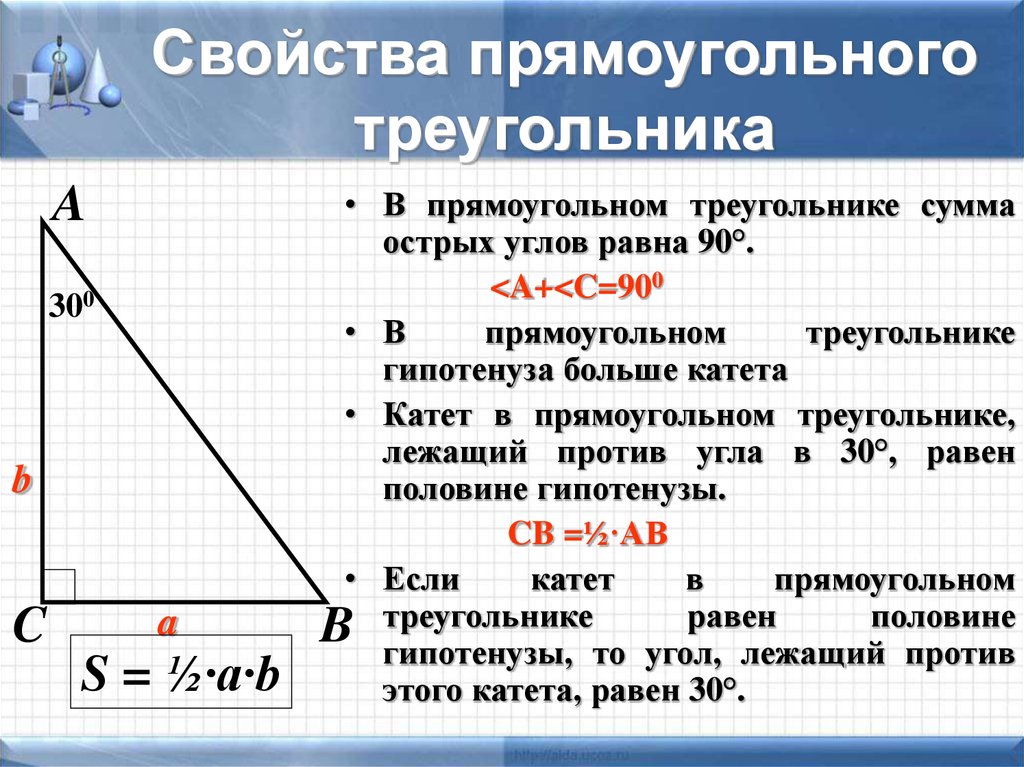
Зная длины сторон прямоугольного треугольника, вы можете использовать теорему Пифагора для расчета углов.

Помните, что сумма углов в любом треугольнике всегда равна 180 градусам, а в прямоугольном треугольнике один угол всегда равен 90 градусам.

Используйте калькулятор для точного расчета углов, если известны длины сторон.

Для нахождения углов можно использовать таблицы тригонометрических значений.

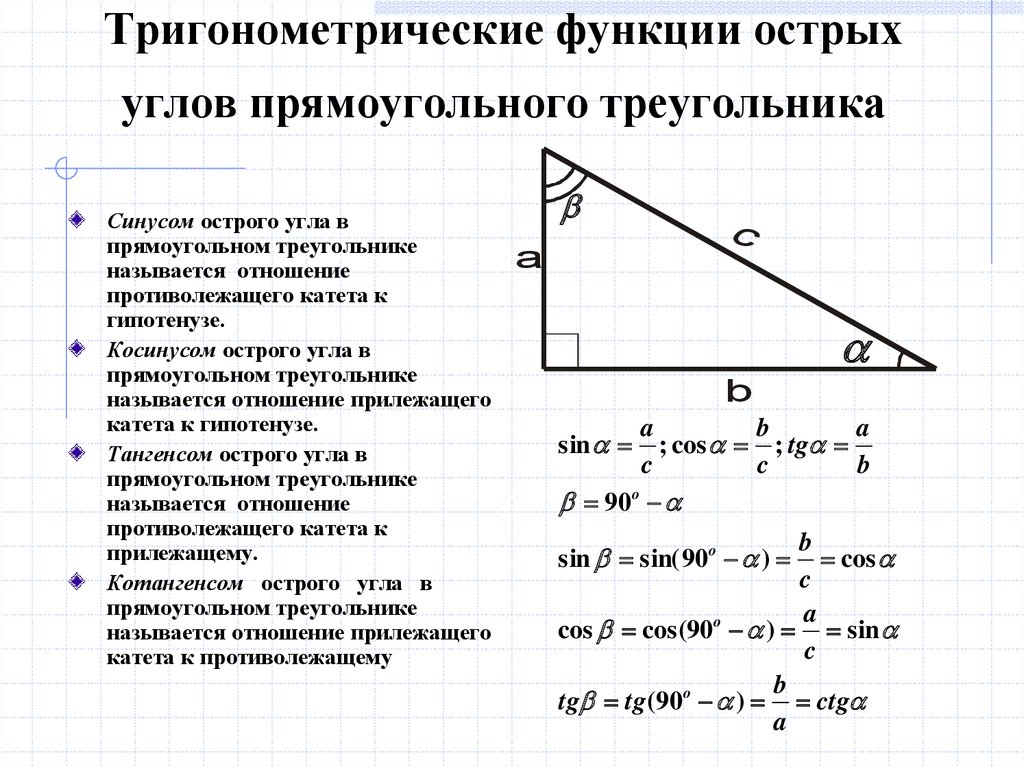
Если известны два угла, третий угол можно найти, вычтя сумму известных углов из 180 градусов.

Практикуйте решение задач на нахождение углов, чтобы лучше понимать тригонометрию и геометрию.

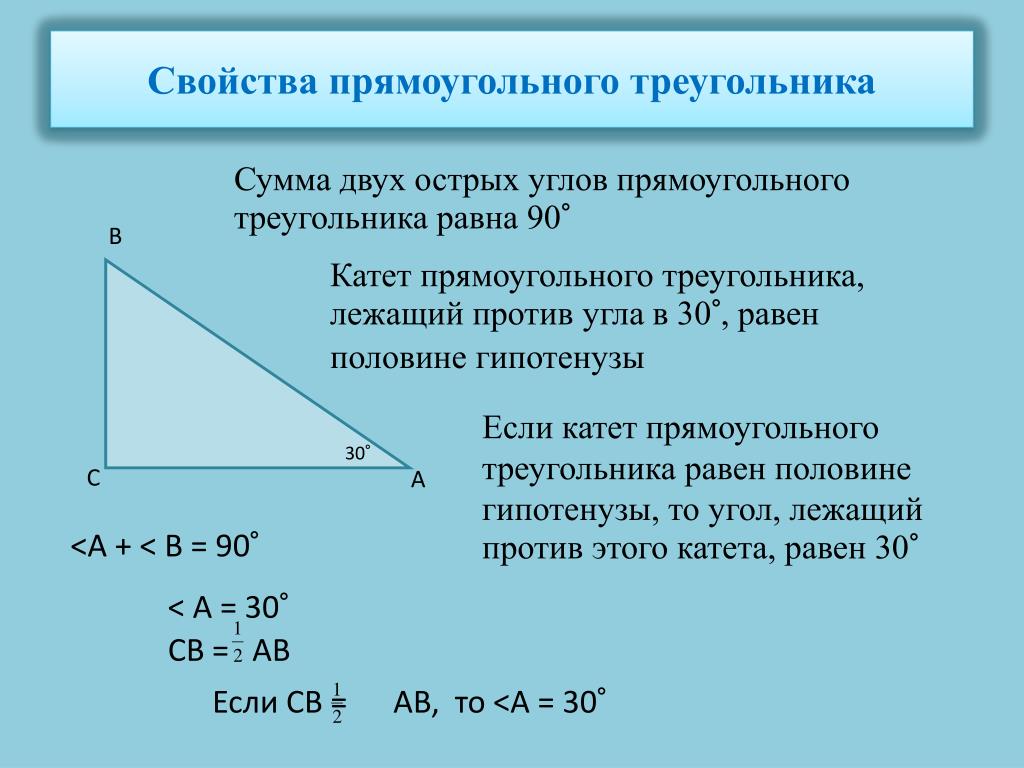
Используйте онлайн-ресурсы и приложения для изучения методов нахождения углов в треугольниках.

Решайте задачи с различными условиями для закрепления знаний.

Всегда проверяйте свои расчеты, чтобы убедиться в их правильности.