Методы нахождения пересечения прямой и плоскости по уравнениям
В этой статье мы рассмотрим способы нахождения точки пересечения прямой и плоскости, используя различные математические подходы и уравнения. Данный процесс важен в геометрии и аналитической геометрии, а также находит применение в различных областях науки и техники.


Начните с записи уравнений прямой и плоскости в параметрической форме.
Найти точку пересечения прямой и плоскости
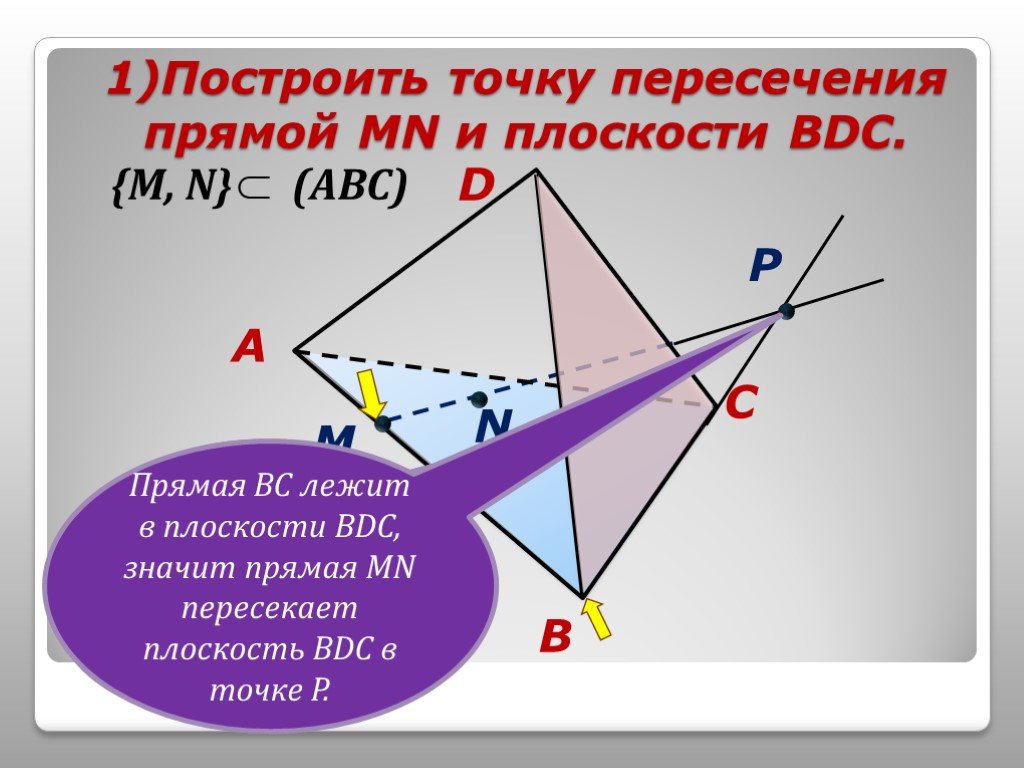
Преобразуйте уравнения так, чтобы выразить координаты точки пересечения через параметр t.
Пересечение прямой и плоскости


Решите систему уравнений, приравняв координаты точки пересечения.
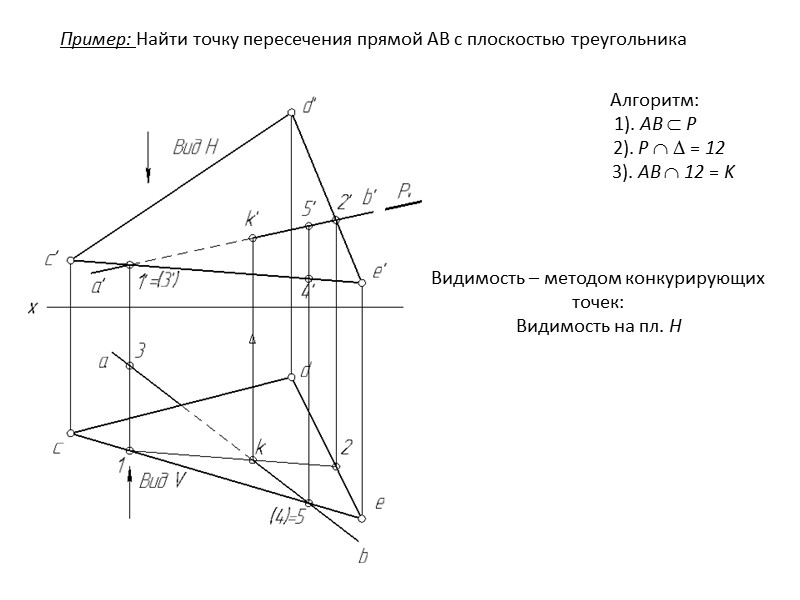
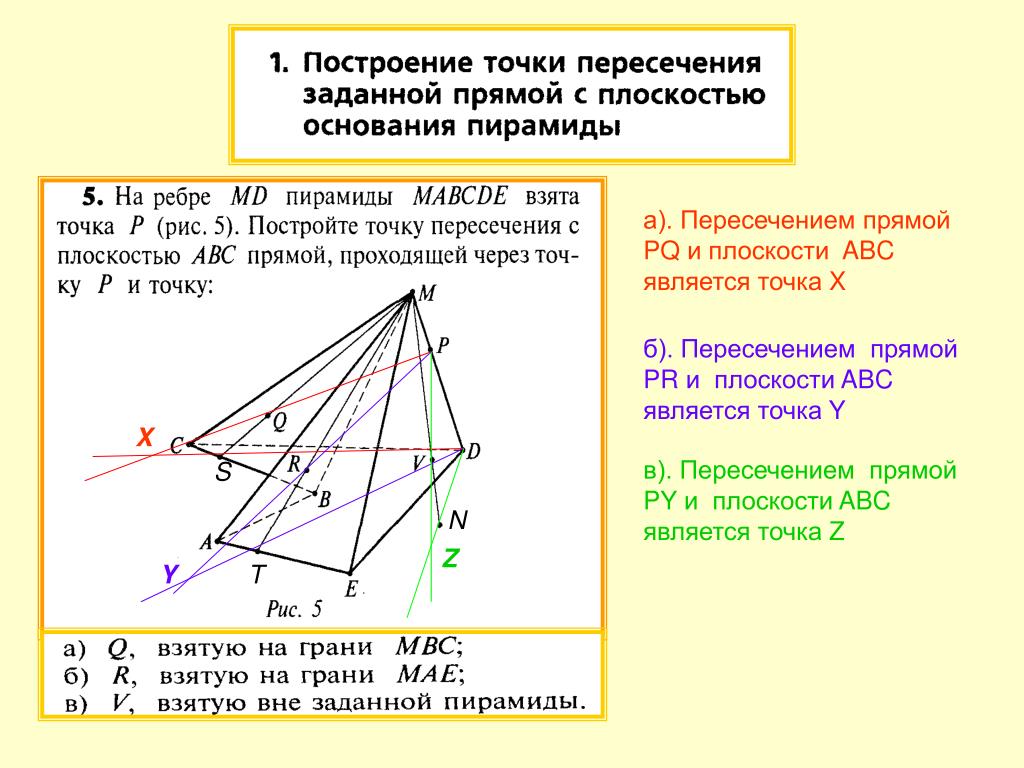
Используйте метод подстановки для нахождения значений параметра t.

После нахождения параметра t, подставьте его значение обратно в уравнение прямой.


Полученные координаты и будут точкой пересечения прямой и плоскости.
Проверьте решение, подставив координаты точки в уравнение плоскости.


Если уравнение плоскости выполняется, значит точка пересечения найдена верно.
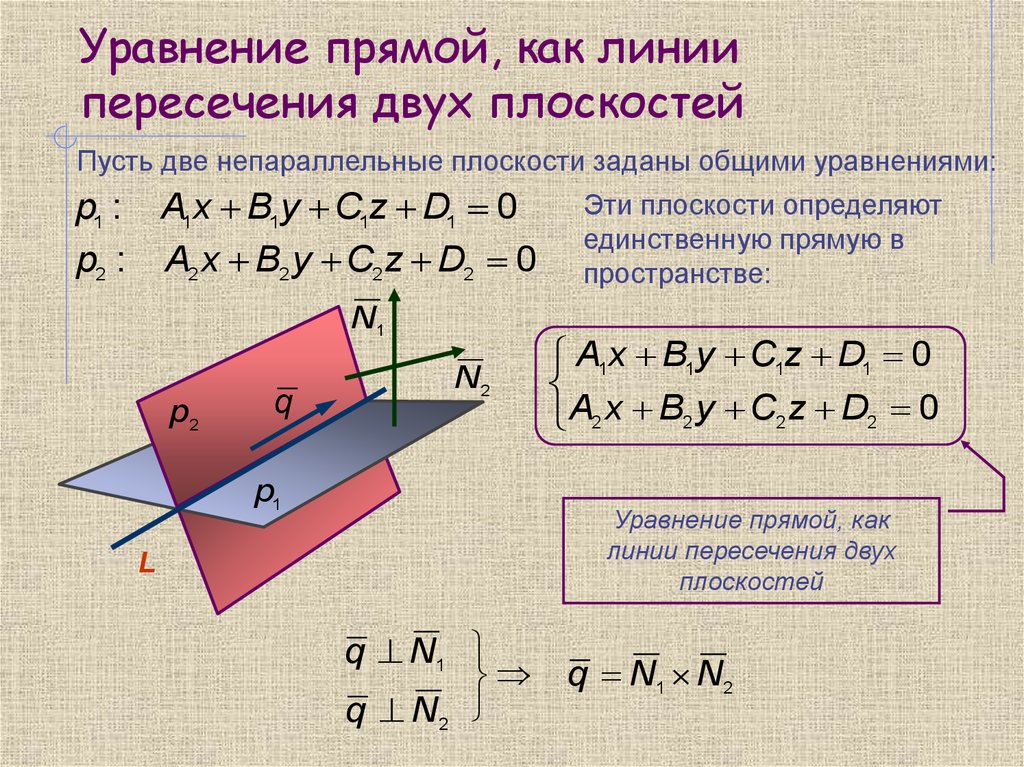

Используйте математическое ПО для автоматизации расчетов.

При сложных уравнениях обратитесь к специализированным учебникам по аналитической геометрии.