Уравнение нормали к графику функции: пошаговое объяснение

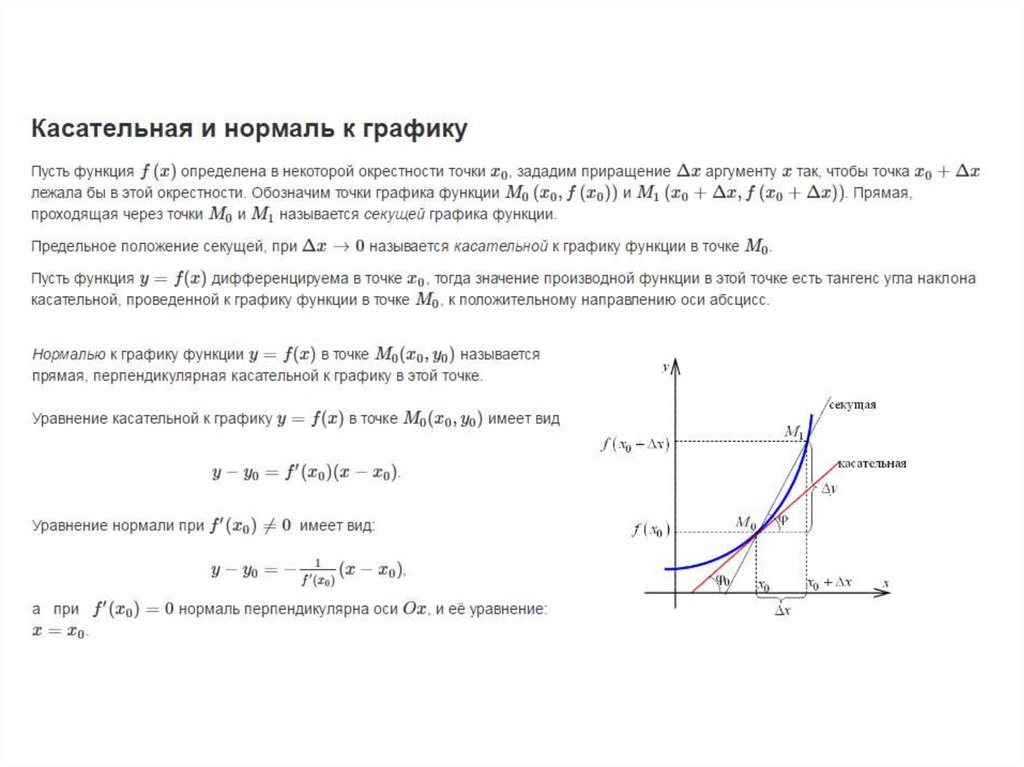
Нормаль к графику функции в точке определяется уравнением, которое можно вывести, зная производную функции в этой точке. В этом руководстве вы найдете полезные советы и примеры, которые помогут вам понять и применить эти знания на практике.

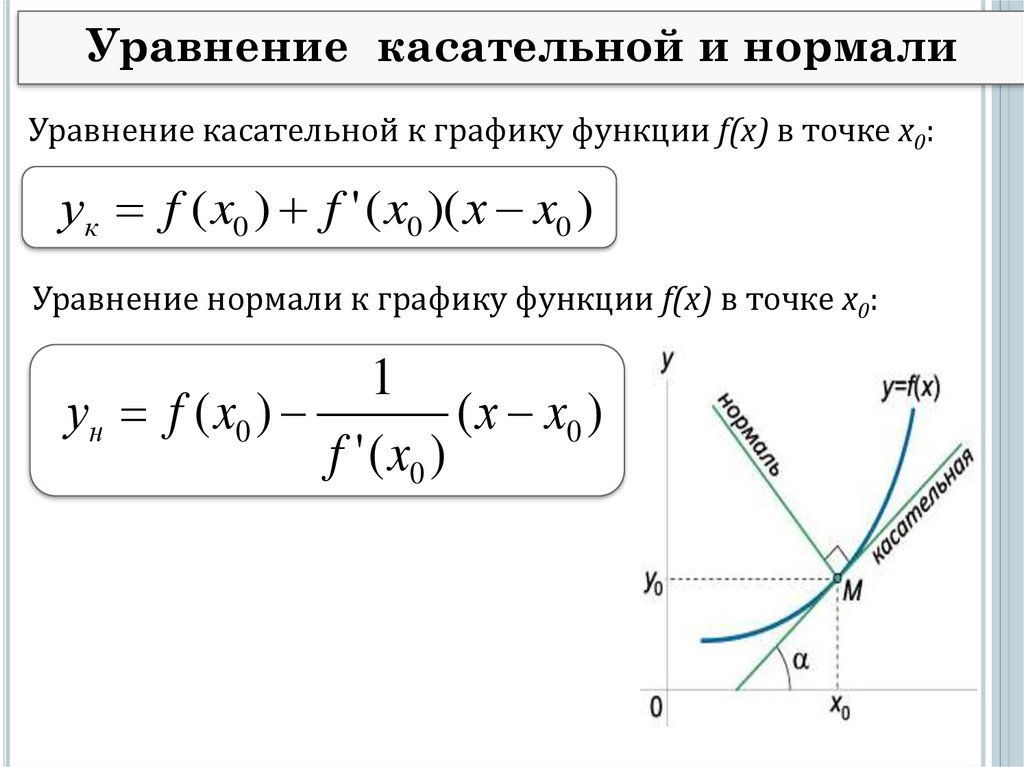
Для начала найдите производную функции в заданной точке.

Производная функции в точке дает вам наклон касательной линии.

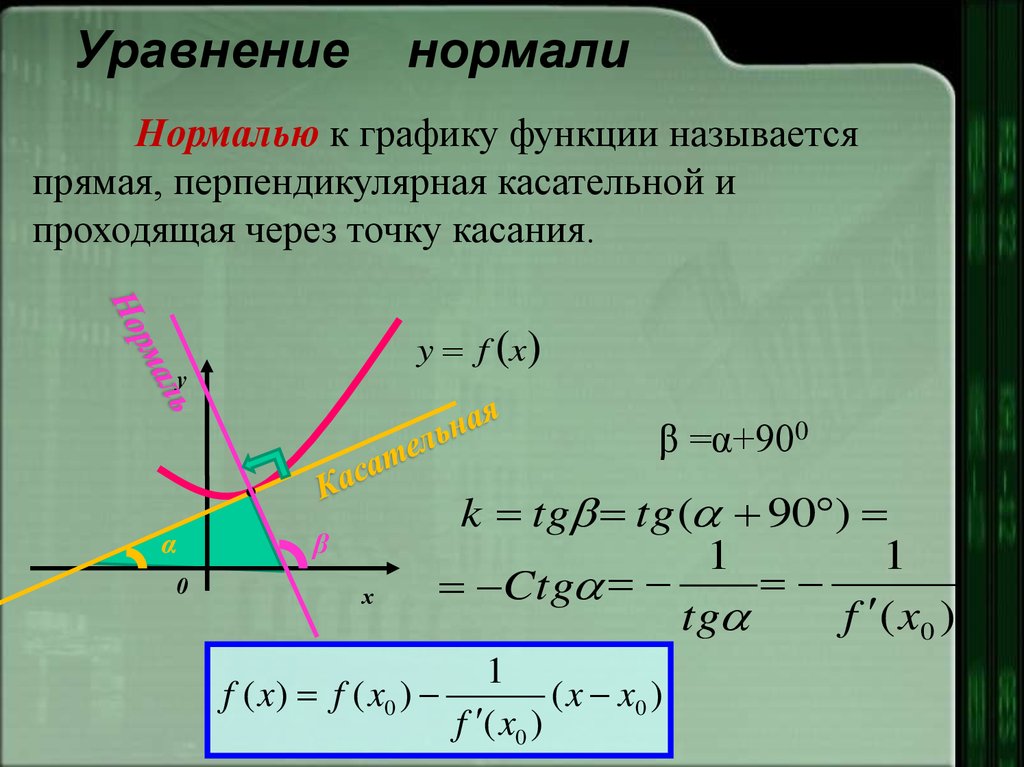
Чтобы найти наклон нормали, возьмите отрицательный обратный наклон касательной.

Используйте уравнение прямой линии: y = mx + b, где m - это наклон нормали, а b - точка пересечения с осью y.

Найдите точку пересечения нормали с осью y, подставив координаты точки в уравнение.

Проверьте полученное уравнение нормали, чтобы убедиться в его правильности.

Используйте графический калькулятор для визуализации нормали и функции.

Практикуйтесь на разных функциях, чтобы лучше понять процесс нахождения нормали.

Изучайте примеры из учебников и онлайн-ресурсов для углубленного понимания.

Помните, что нормаль всегда перпендикулярна касательной в данной точке.