Вычисление площади диагонального сечения параллелепипеда: советы и примеры
На этой странице вы найдете полезные советы и пошаговые инструкции по вычислению площади диагонального сечения параллелепипеда. Фотографии и примеры помогут вам лучше понять процесс.
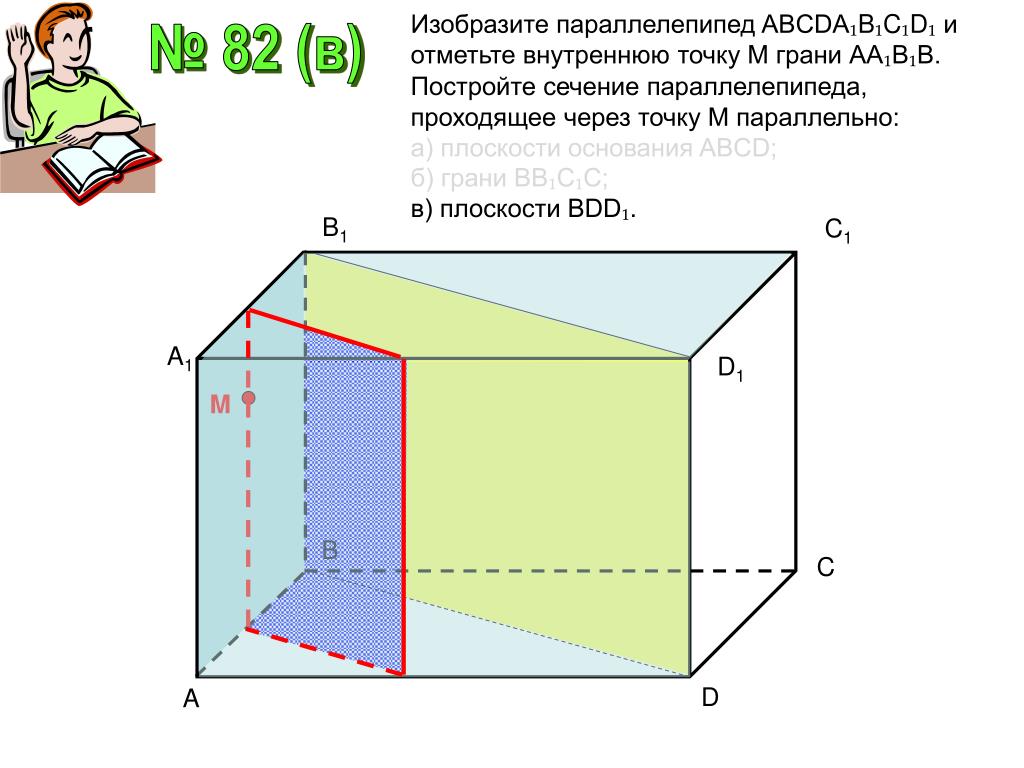
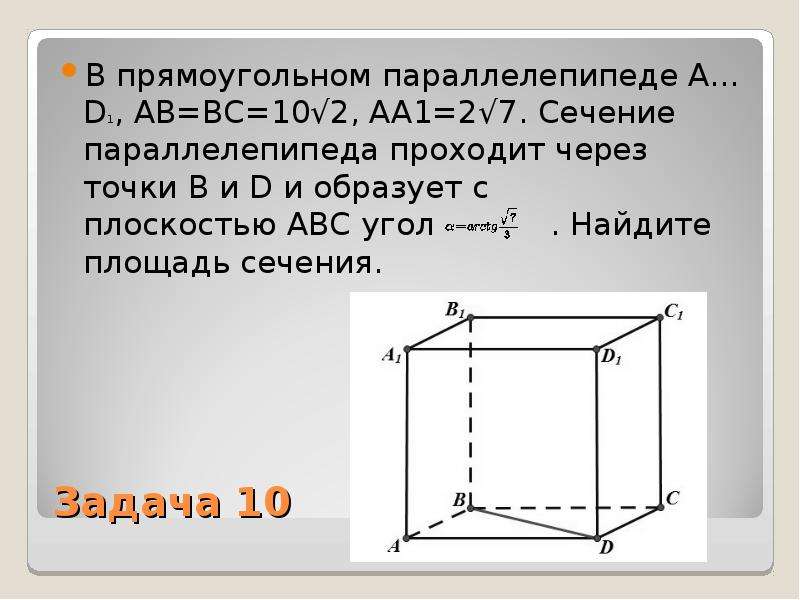
Определите длины всех ребер параллелепипеда, они необходимы для дальнейших расчетов.
№113. По какой прямой пересекаются плоскости сечений A1BCD1 и BDD1B1 параллелепипеда ABCDA1B1C1D1?

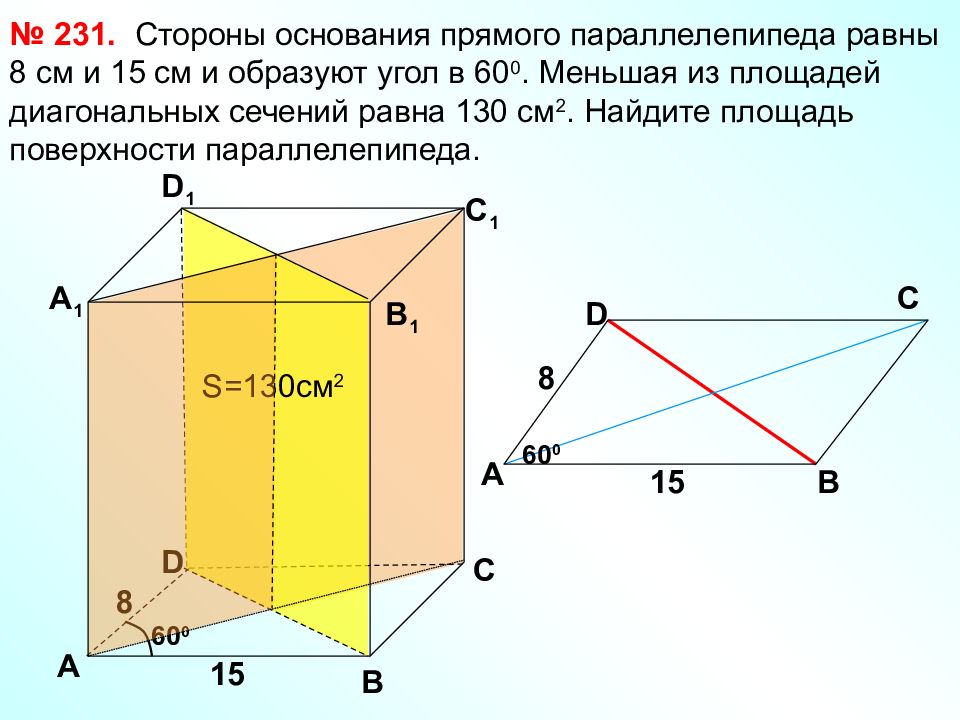
Для вычисления диагонального сечения используйте теорему Пифагора в трех измерениях.
Призма. Площадь диагонального сечения. Теорема Пифагора в стереометрии.
Запишите формулу диагонали параллелепипеда: d=a2+b2+c2d = /sqrt{a^2 + b^2 + c^2}d=a2+b2+c2.
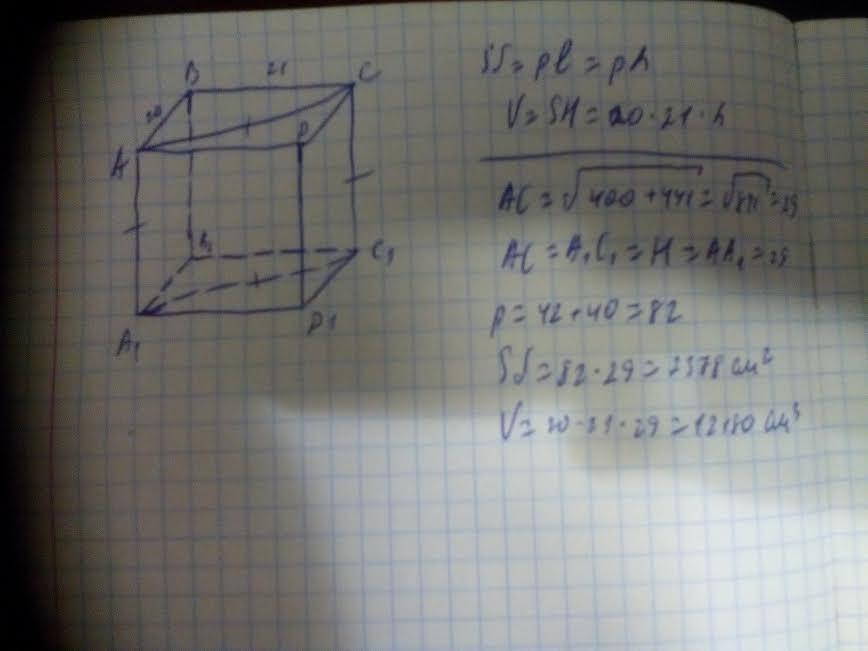
Вычислите длину диагонали, подставив известные значения сторон.

Определите высоту сечения, проведенного через диагональ.
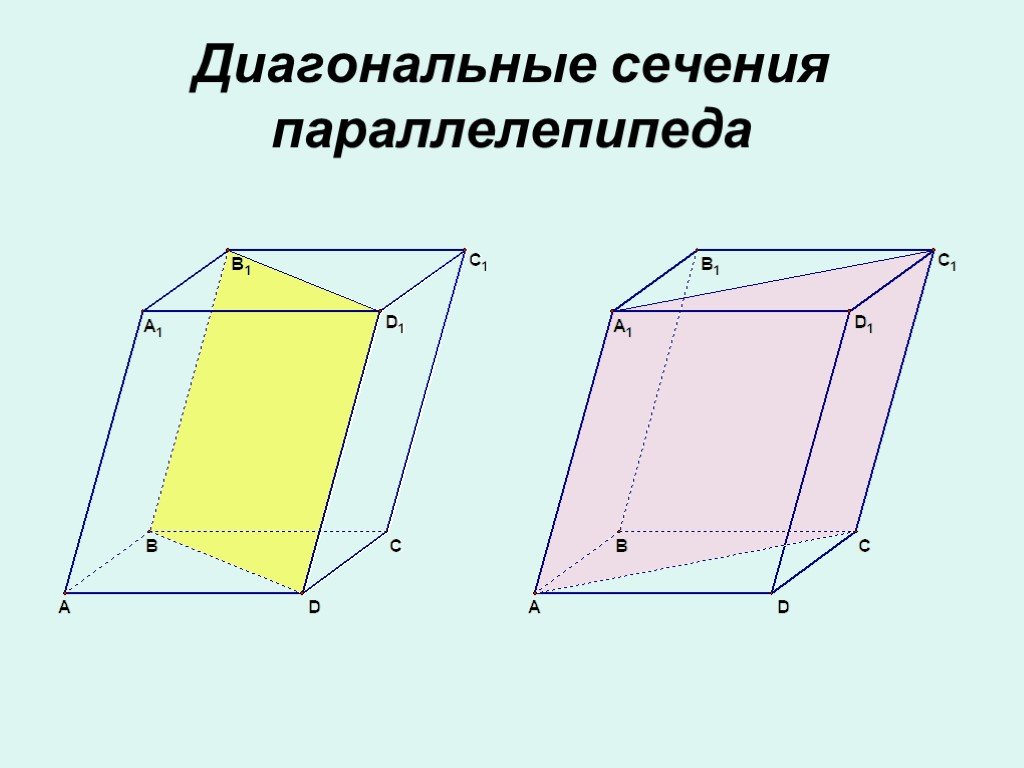
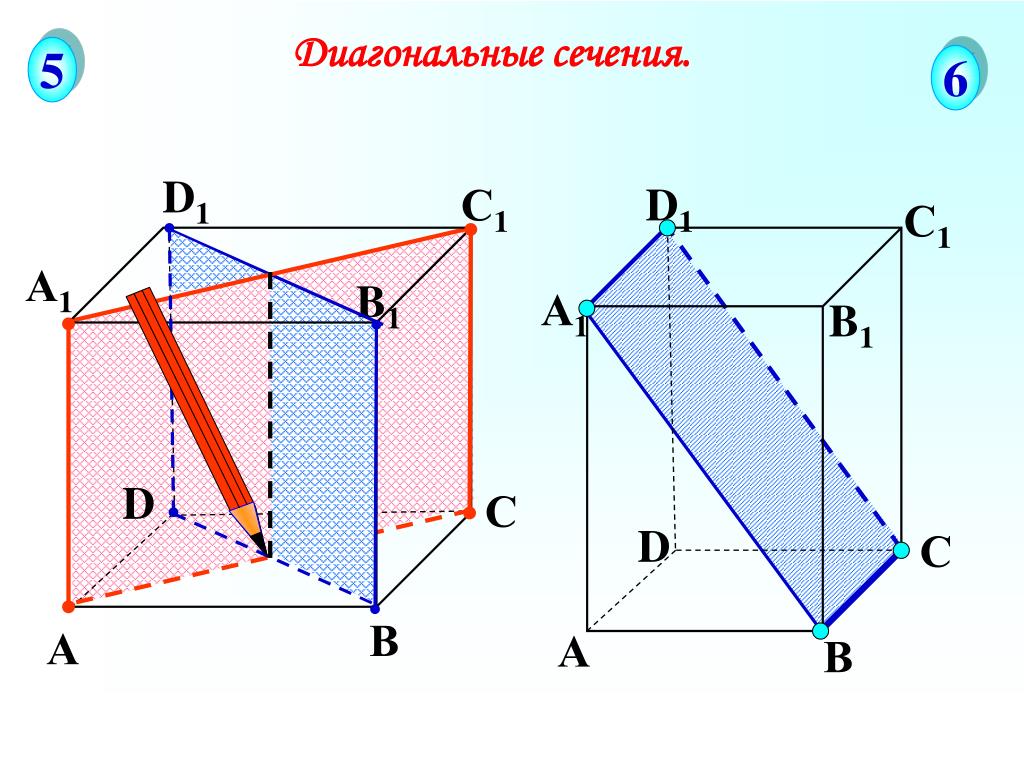
Используйте формулу площади для треугольника: S=12⋅base⋅heightS = /frac{1}{2} /cdot base /cdot heightS=21⋅base⋅height.
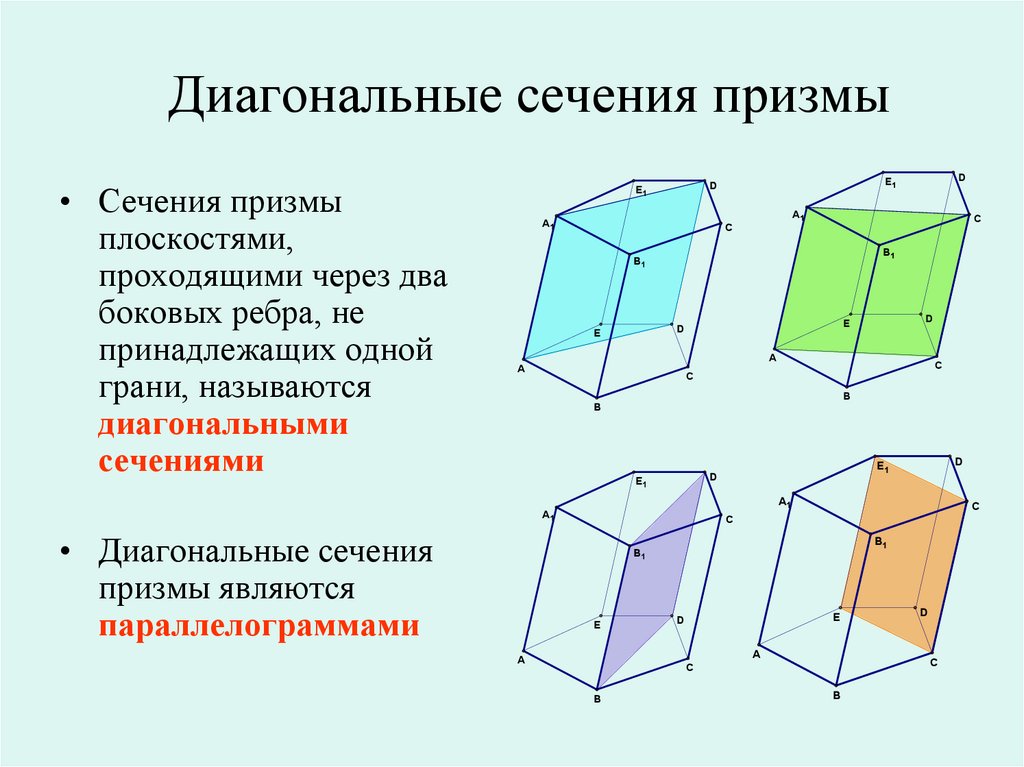
Если параллелепипед правильный, его диагональные сечения будут равносторонними треугольниками.
Используйте геометрические свойства параллелепипеда для упрощения расчетов.

Проверяйте промежуточные результаты, чтобы избежать ошибок.
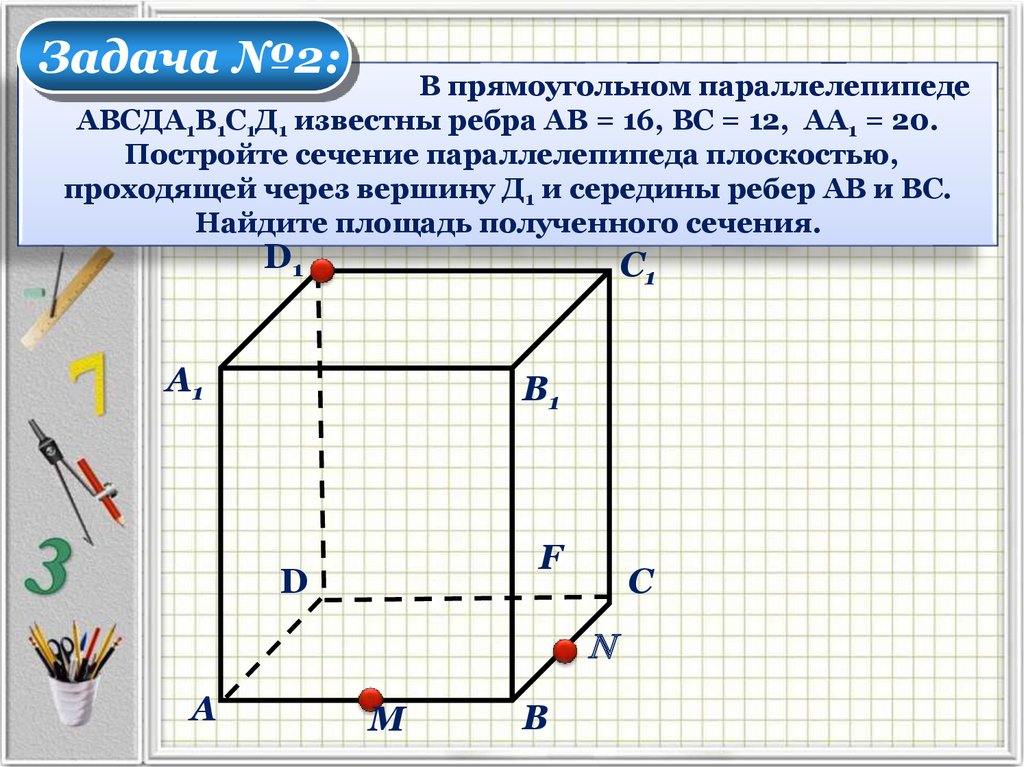
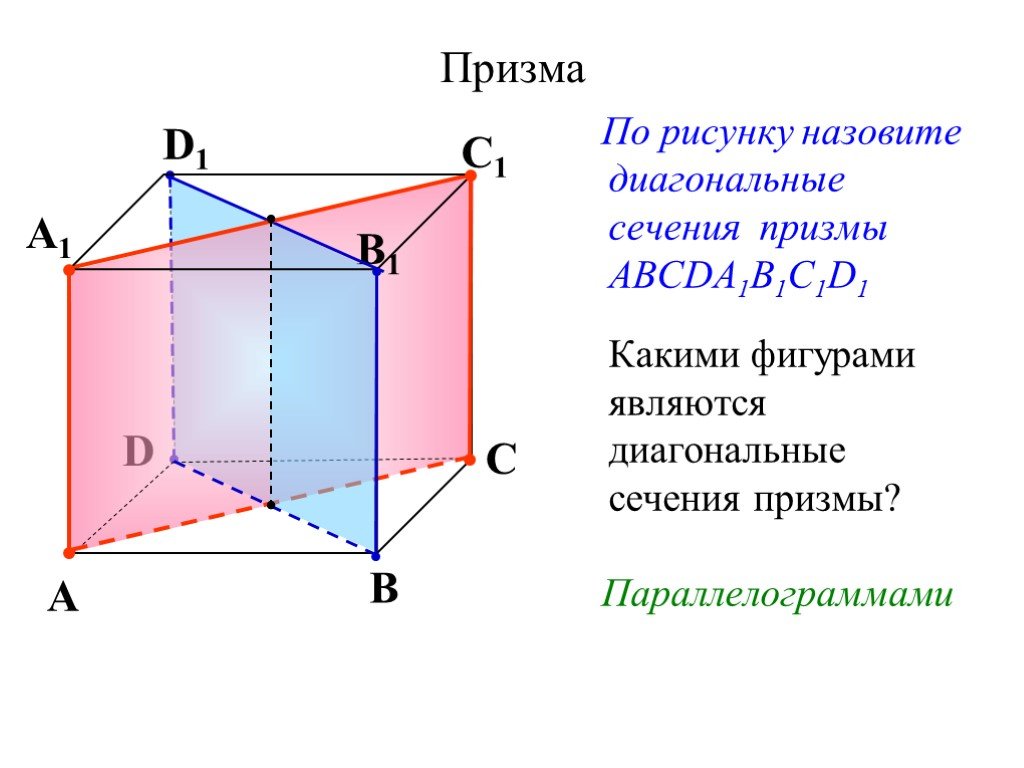
Практикуйтесь на различных примерах, чтобы закрепить знания и навыки.