Площадь закрашенной фигуры: интегралы и их применение
В этом разделе мы рассмотрим, как можно использовать интегралы для вычисления площади закрашенной фигуры. Мы обсудим основные методы и представим наглядные примеры, которые помогут лучше понять процесс вычисления. Этот подход позволяет находить площади сложных геометрических фигур, которые невозможно вычислить стандартными методами.
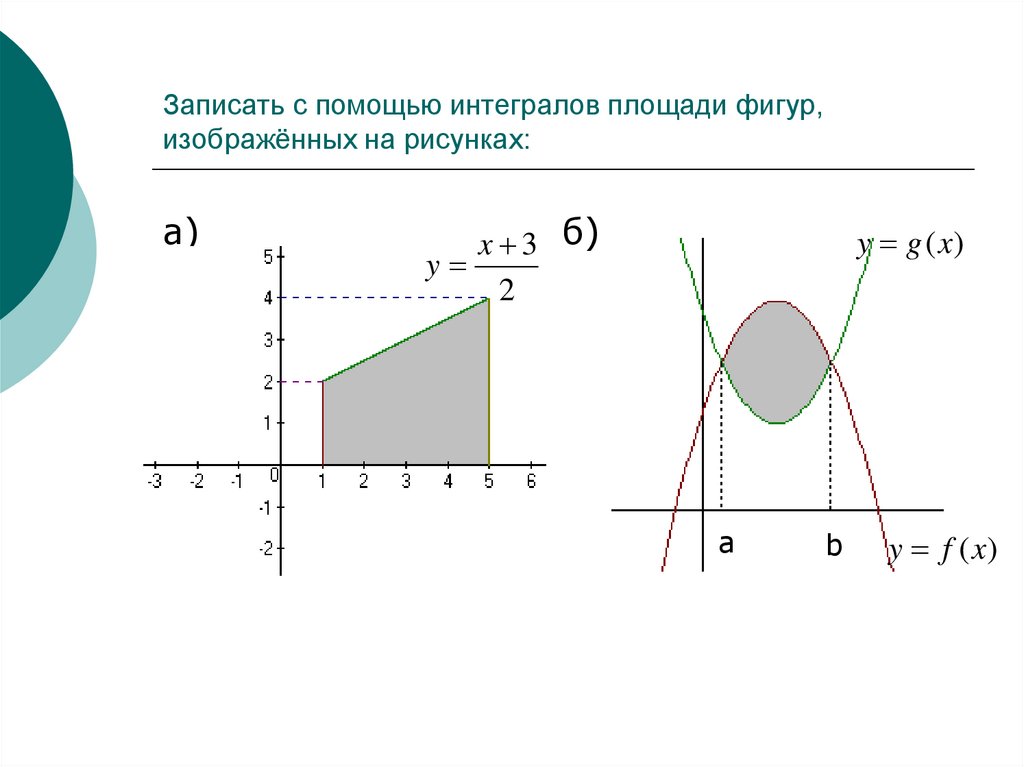
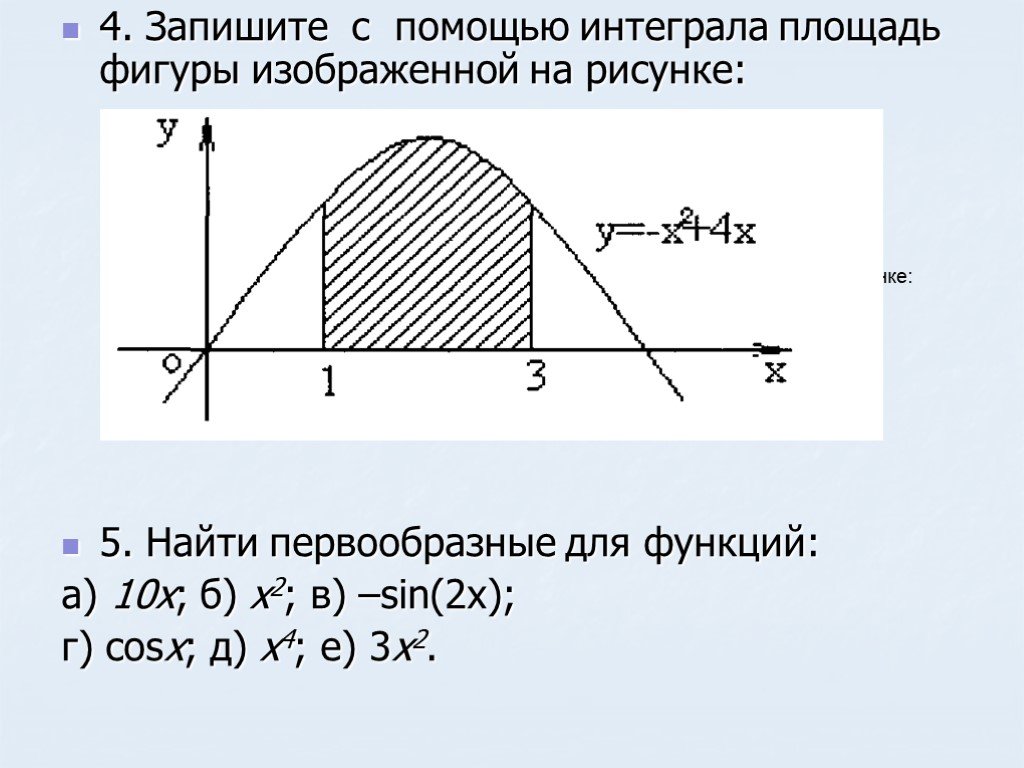
Для начала определите границы интегрирования, которые соответствуют области закрашенной фигуры.
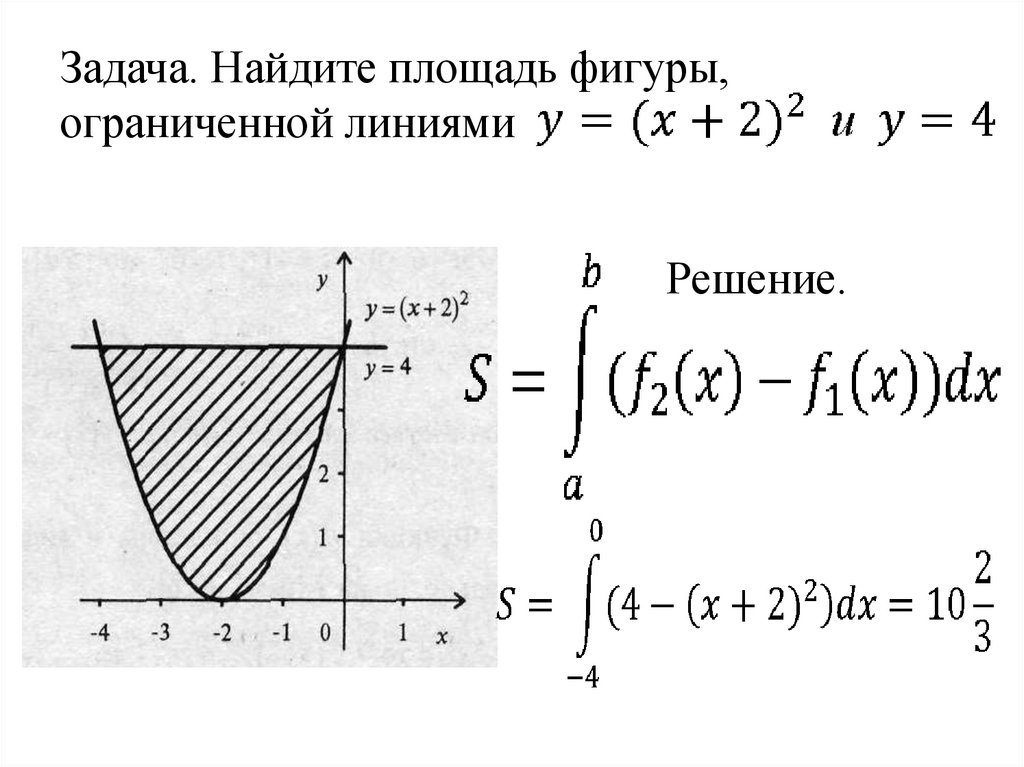
Найти площадь фигуры, ограниченной линиями. Пример 1.
Используйте графики функций для визуализации фигуры и определения ее формы.
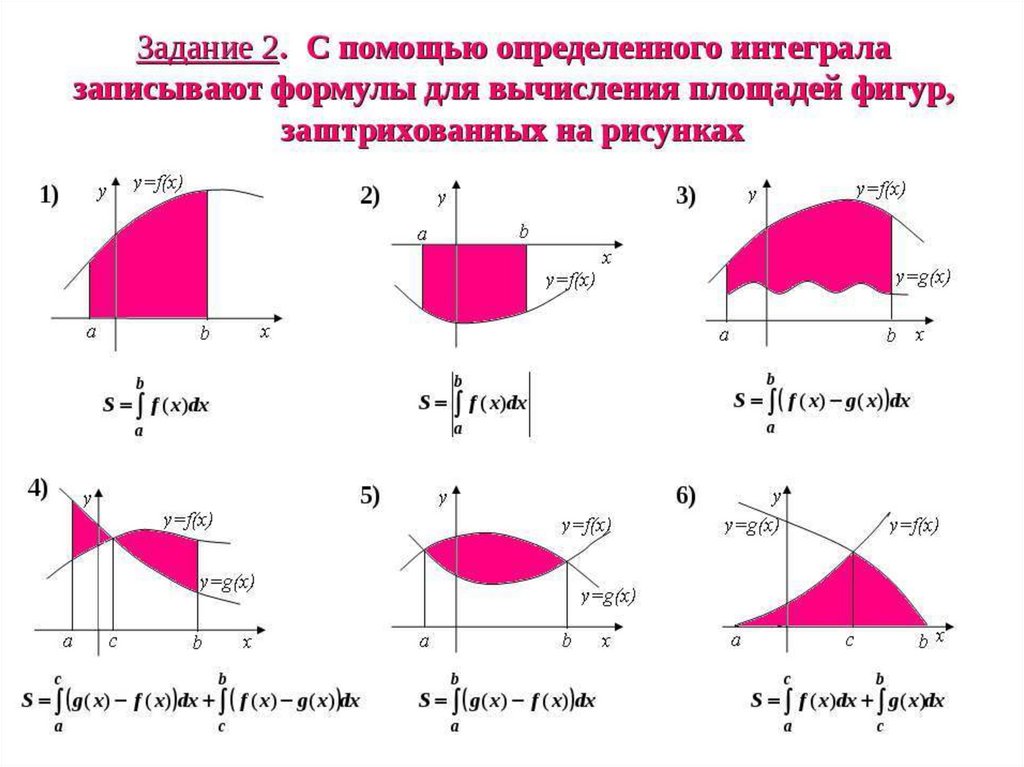
Найдите площадь закрашенной фигуры.
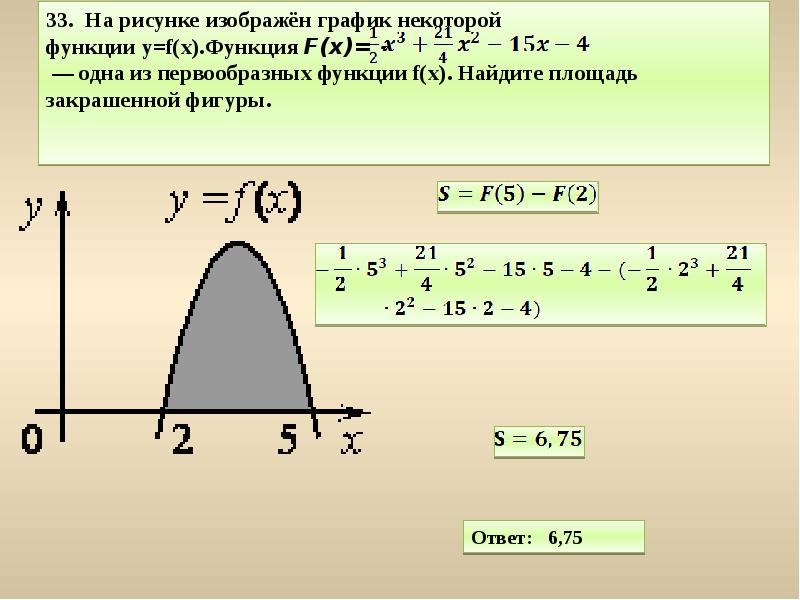
Проверьте, что ваши функции корректно описывают границы фигуры.
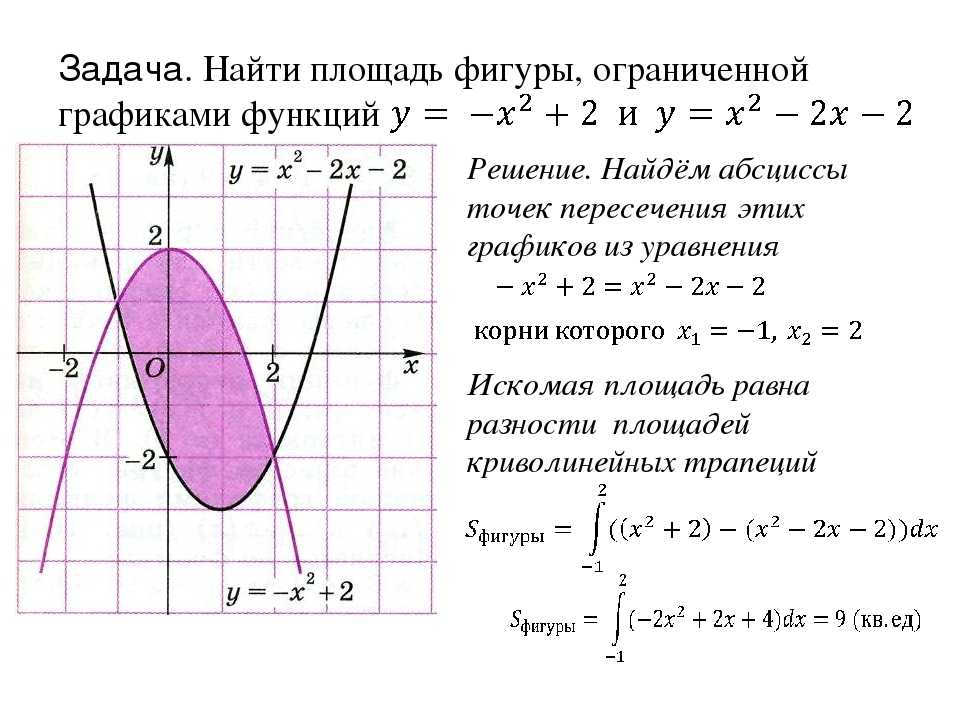
Используйте символьные вычисления для упрощения интегралов, если это возможно.
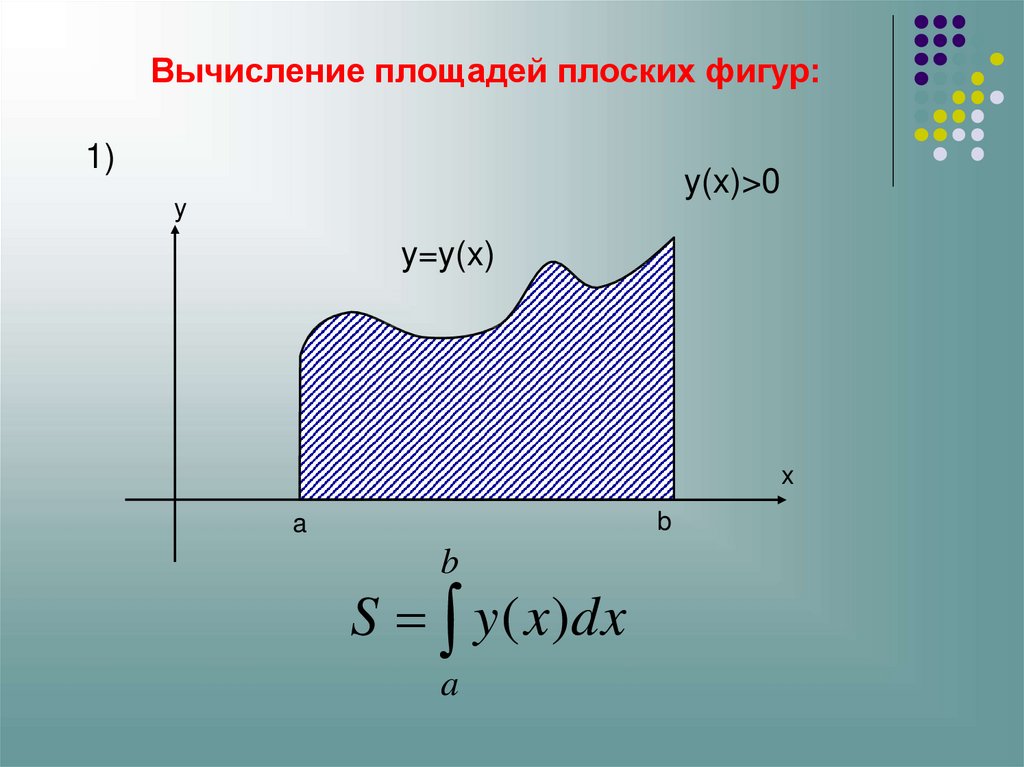
Разбейте сложные интегралы на более простые, если это поможет упростить вычисления.
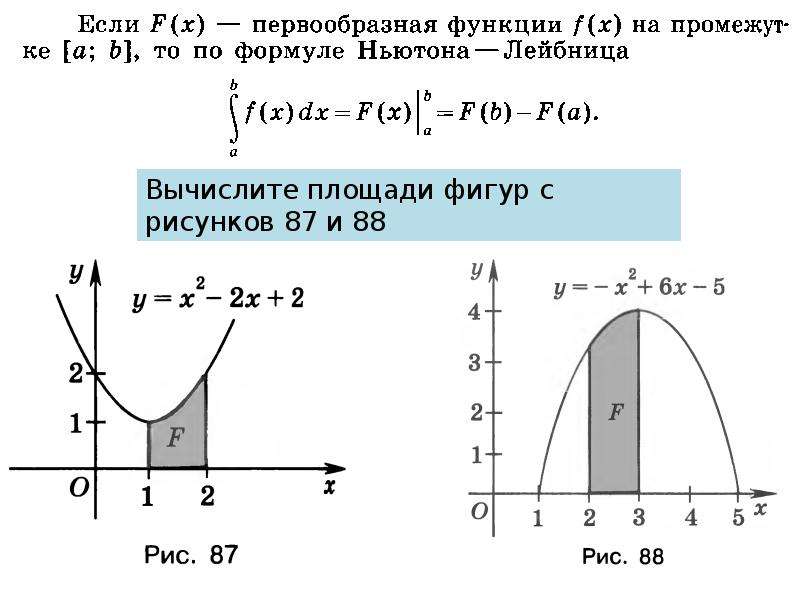
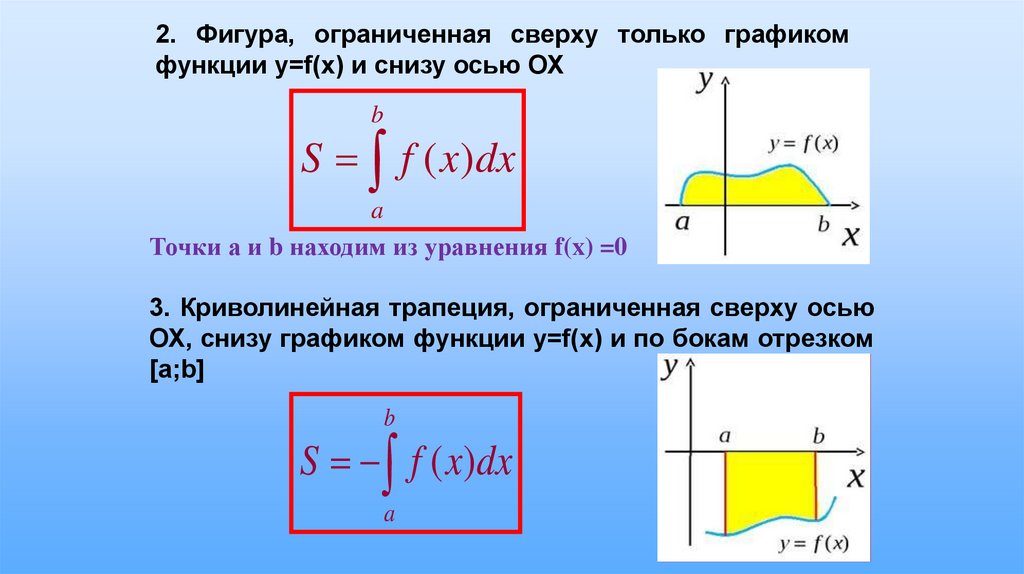
Криволинейная трапеция и ее площадь. 11 класс.


Внимательно проверяйте вычисления, чтобы избежать ошибок в окончательных результатах.

Используйте численные методы, если аналитическое решение интеграла трудно найти.

Убедитесь, что ваши результаты имеют смысл и соответствуют геометрическим ожиданиям.
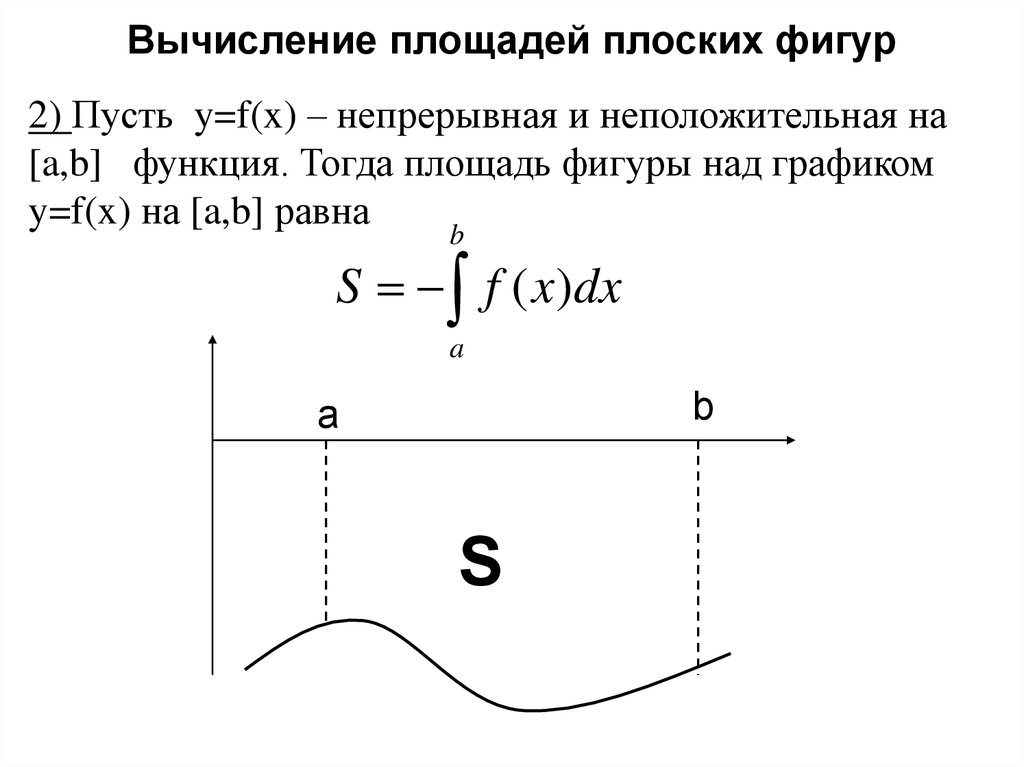
Практикуйтесь на различных примерах, чтобы лучше освоить метод интегрирования.
Нахождение площадей фигур, ограниченных графиками
Обратитесь к учебникам и онлайн-ресурсам для углубленного изучения темы.