Простое руководство по разложению вектора на базисные компоненты
Разложение вектора по базису — это важный навык в линейной алгебре и геометрии. В этой статье вы найдете пошаговые инструкции и полезные советы, которые помогут вам освоить этот метод.

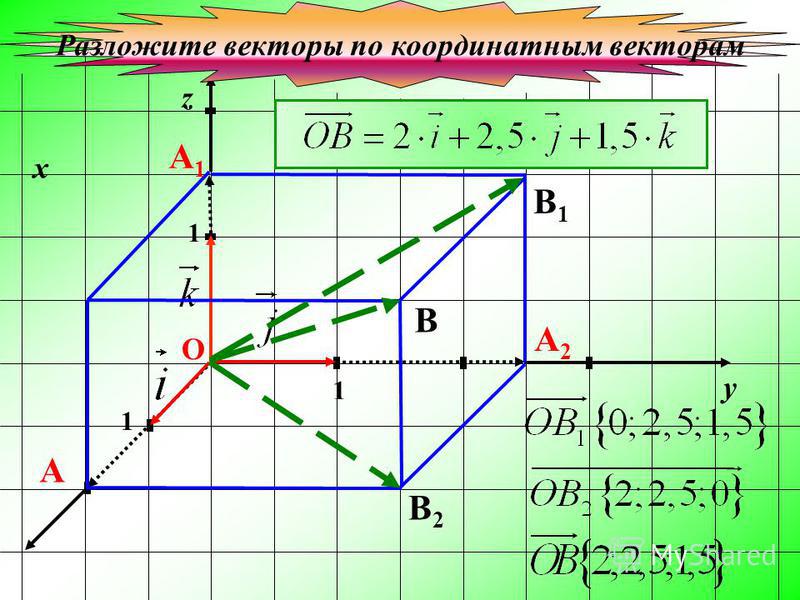

Начните с определения базиса, к которому будет приведен вектор. Обычно это стандартный базис (единичные векторы).
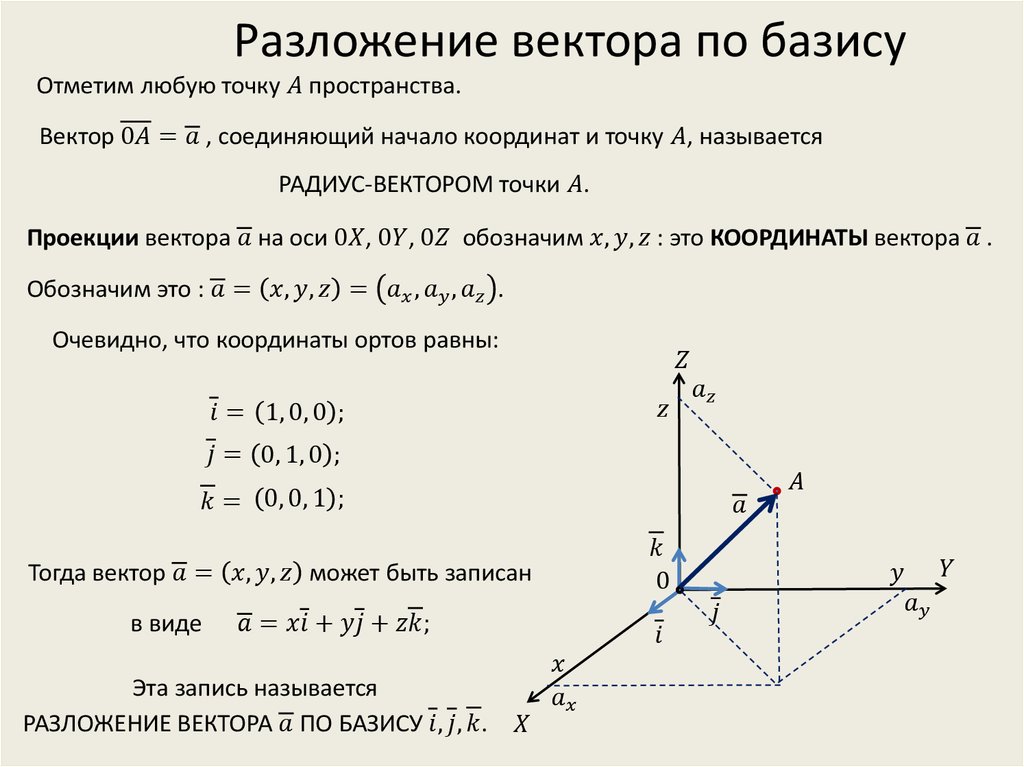
Запишите ваш вектор в координатной форме. Это поможет визуализировать процесс.

Используйте метод проекции для нахождения координат вектора в выбранном базисе.
Базис. Разложение вектора по базису.
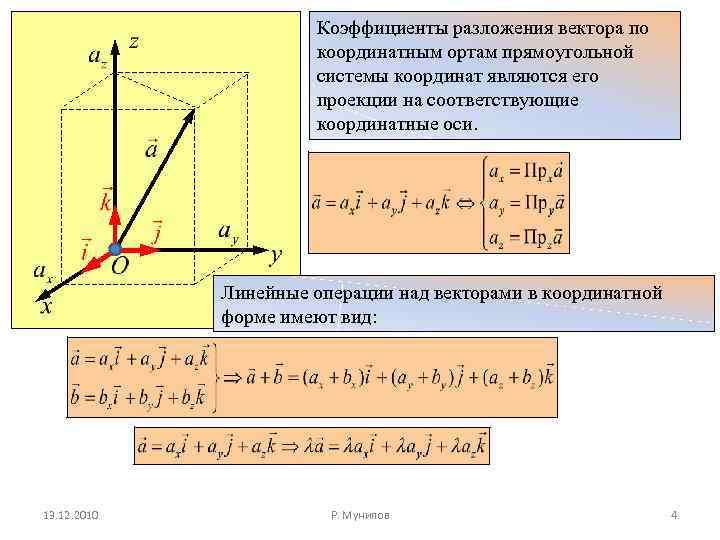
Проверьте правильность расчетов, сложив полученные компоненты и убедившись, что они дают исходный вектор.
Разложение вектора по двум неколлинеарным векторам. Координаты вектора. 9 класс

Не забывайте проверять, что ваш базис ортонормирован, это значительно упростит вычисления.
Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе
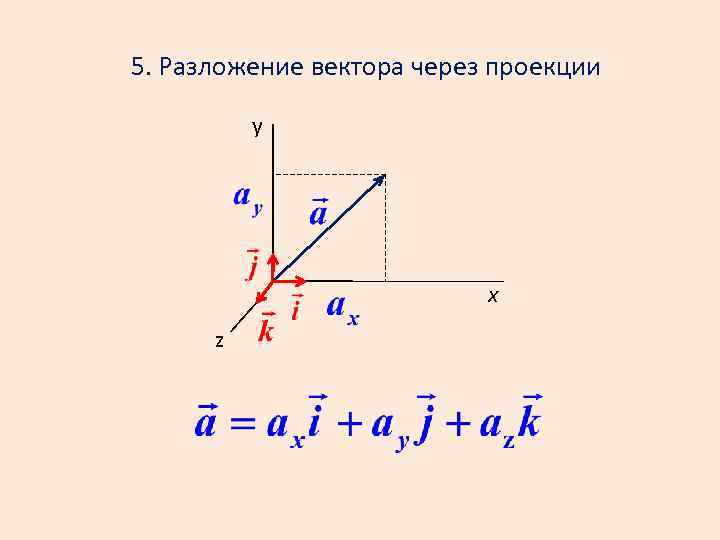
В сложных случаях используйте метод Грамма-Шмидта для ортогонализации базиса.

Для наглядности используйте графические инструменты, такие как координатные плоскости и диаграммы.
Практикуйтесь на простых примерах, чтобы укрепить свои навыки и уверенность в расчетах.
Разложение вектора по векторам (базису). Аналитическая геометрия-1

Воспользуйтесь специализированными программами или калькуляторами для проверки своих результатов.
10 класс, 45 урок, Разложение вектора по трем некомпланарным векторам


Помните, что правильное разложение вектора по базису поможет вам лучше понять структуру векторного пространства.