Как доказать теорему о трех перпендикулярах на практике

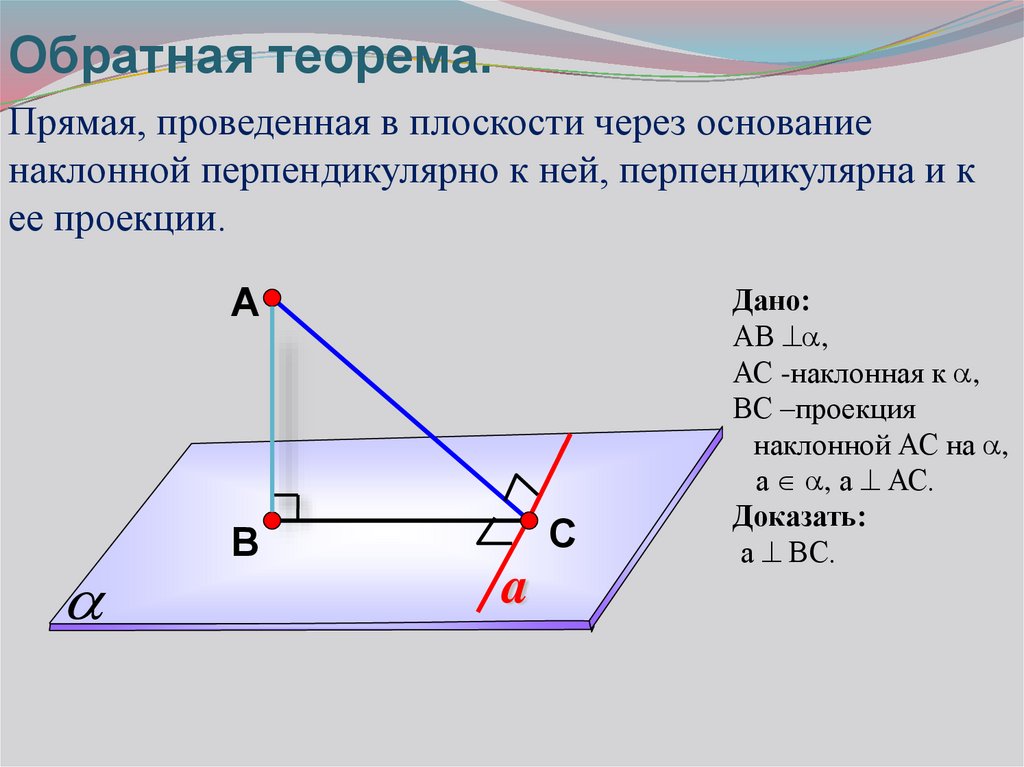
Теорема о трех перпендикулярах является важной частью стереометрии, которая помогает понять взаимное расположение линий и плоскостей в пространстве. Она утверждает, что если из точки на прямой, перпендикулярной плоскости, провести перпендикуляр к этой прямой, то он будет перпендикулярен и к данной плоскости.

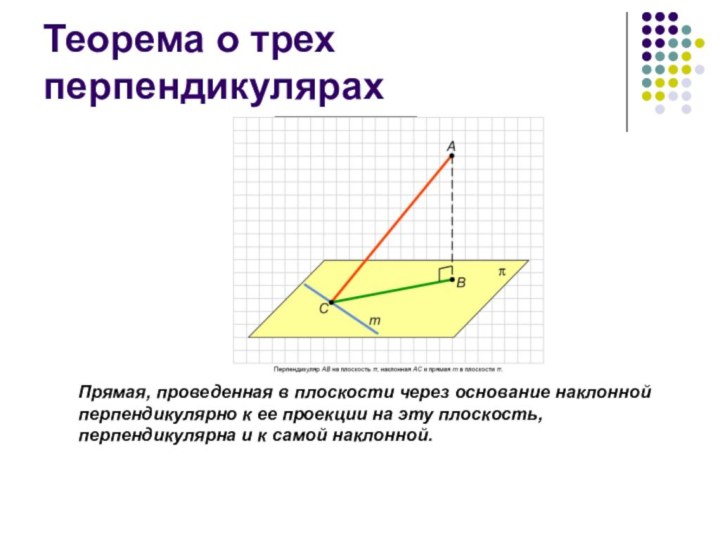
Для лучшего понимания теоремы о трех перпендикулярах, начертите схематический чертеж, отражающий основные элементы: прямую, плоскость и перпендикуляры.

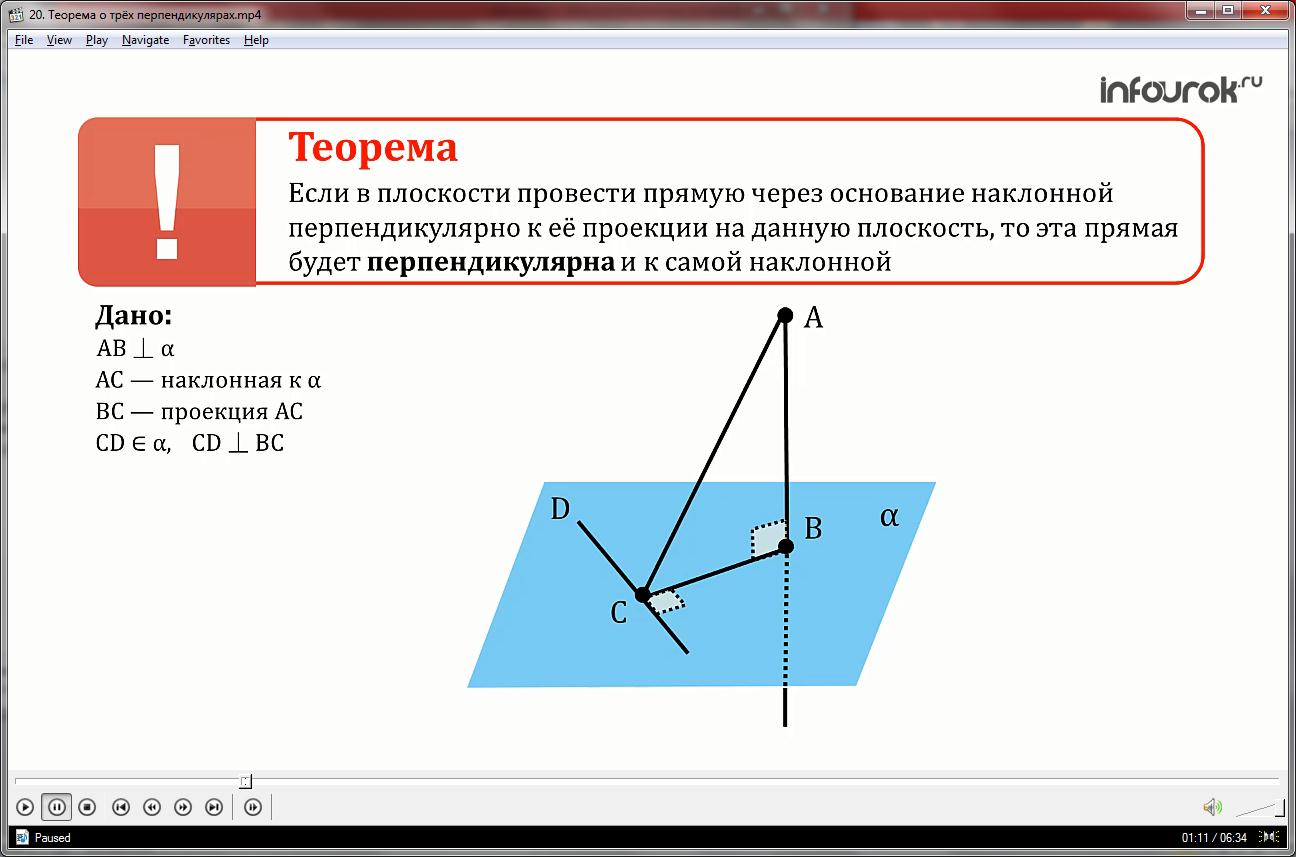
При доказательстве теоремы используйте векторный метод, который наглядно показывает взаимосвязь между линиями и плоскостями.

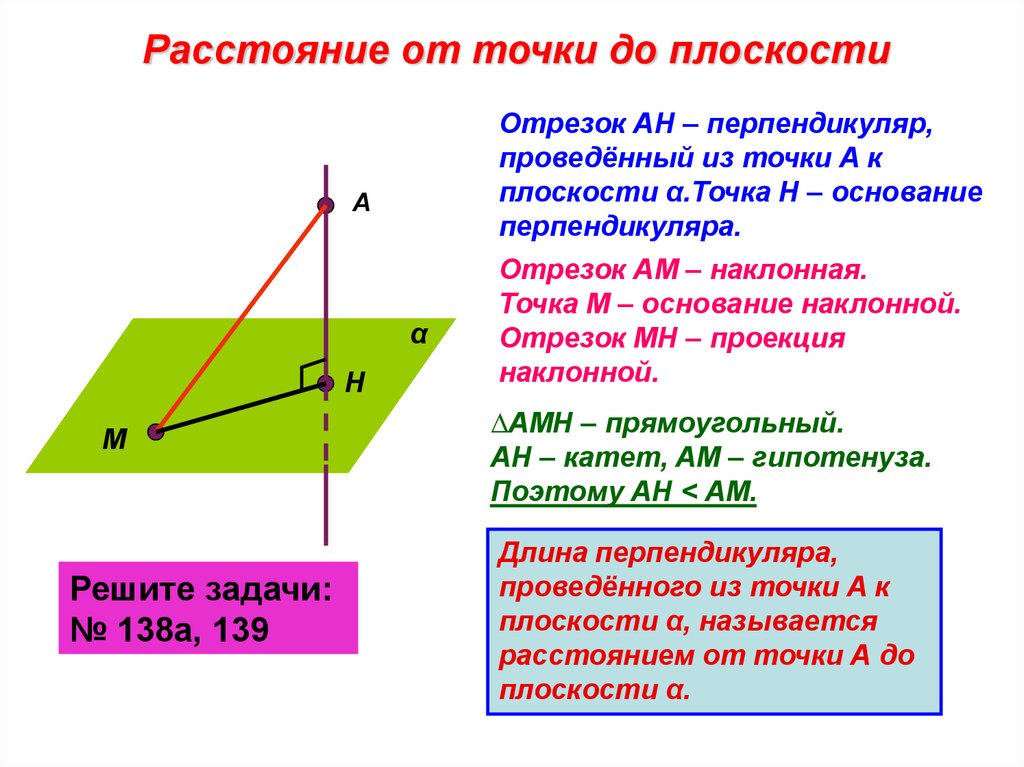
Помните, что точка пересечения перпендикуляра с плоскостью является ключевым элементом, от которого строятся остальные перпендикуляры.

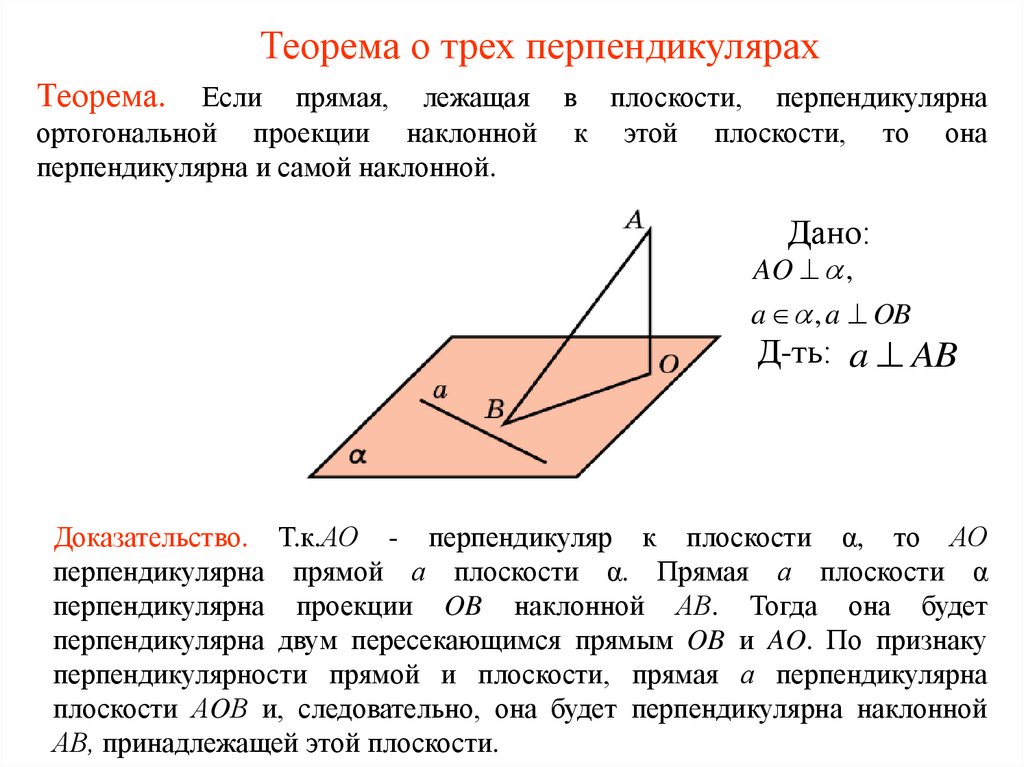
Используйте аналитическую геометрию для более глубокого понимания и доказательства теоремы, работая с уравнениями плоскости и прямой.

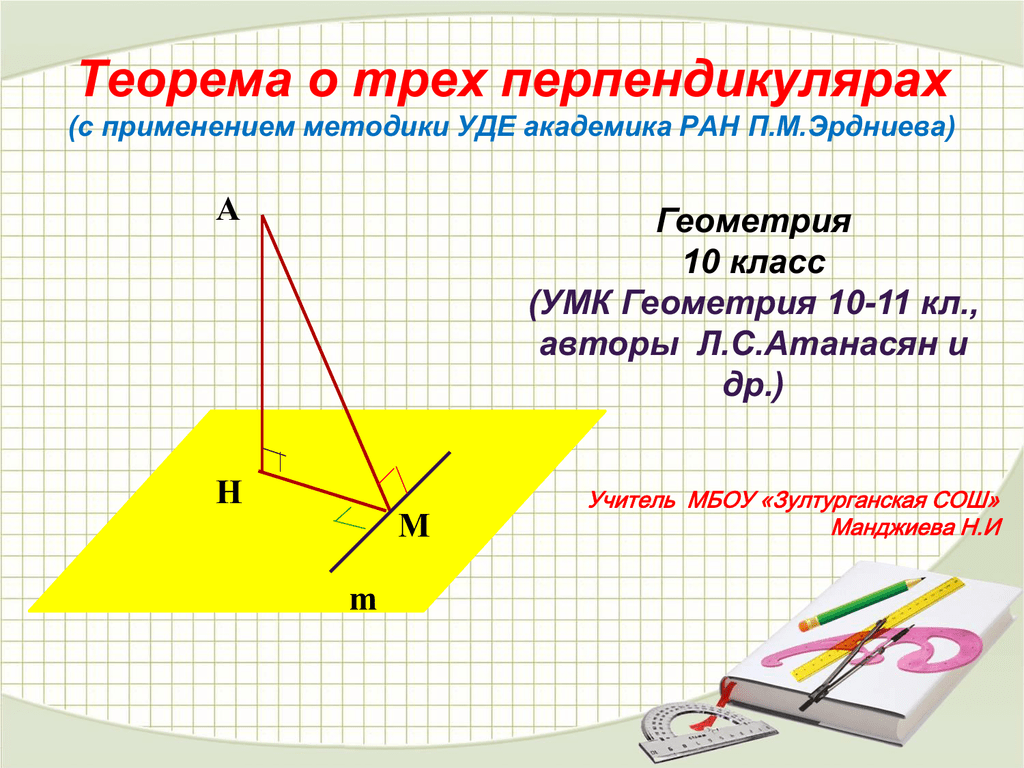
Практикуйтесь в решении задач, связанных с теоремой о трех перпендикулярах, чтобы закрепить теоретические знания на практике.

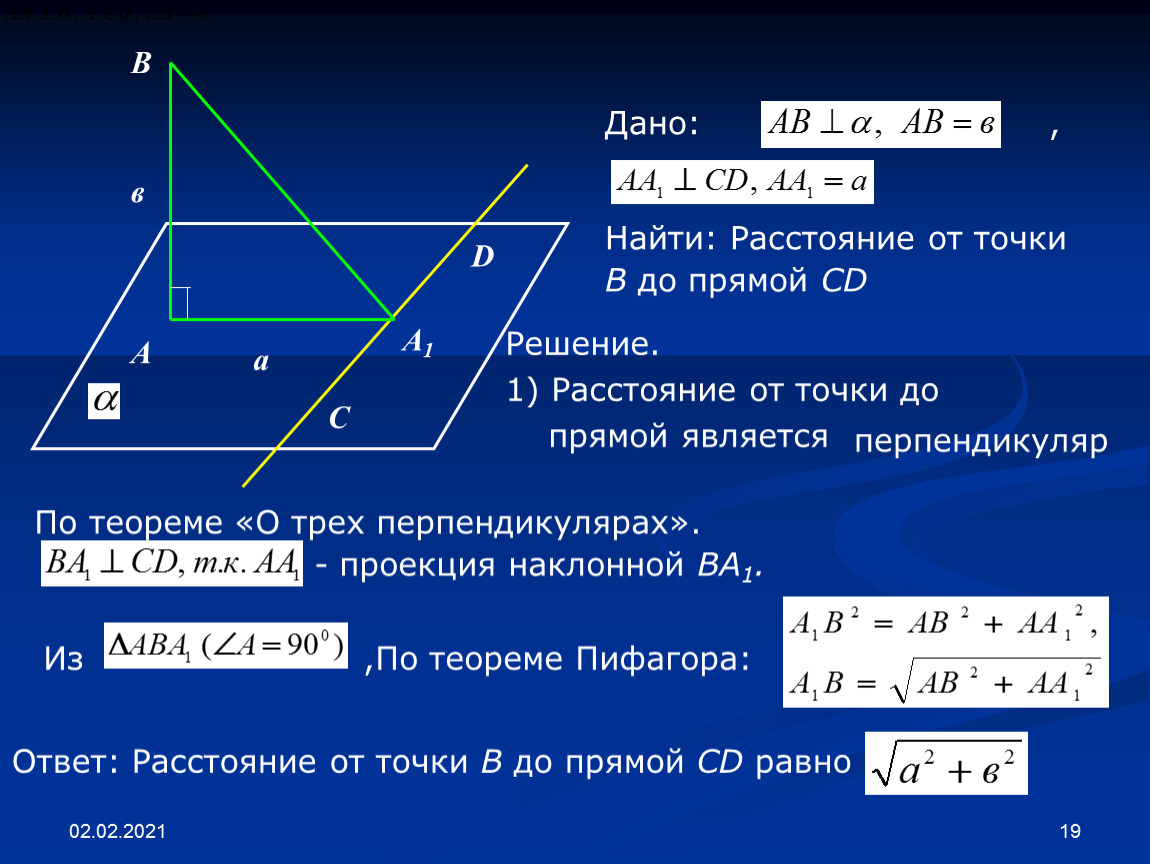
Применяйте теорему о трех перпендикулярах при решении геометрических задач на нахождение углов и расстояний в пространстве.

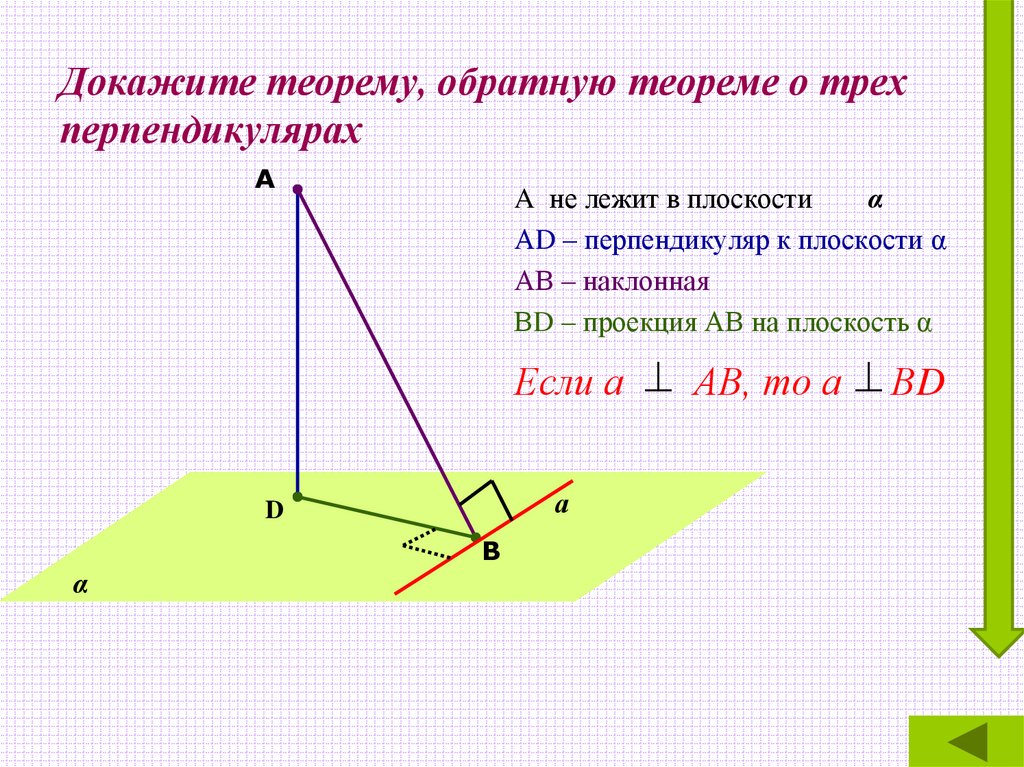
Используйте программные средства, такие как геометрические конструкторы, для визуализации теоремы и проверки своих решений.

Обратитесь к учебникам по стереометрии для получения дополнительных примеров и упражнений по данной теме.

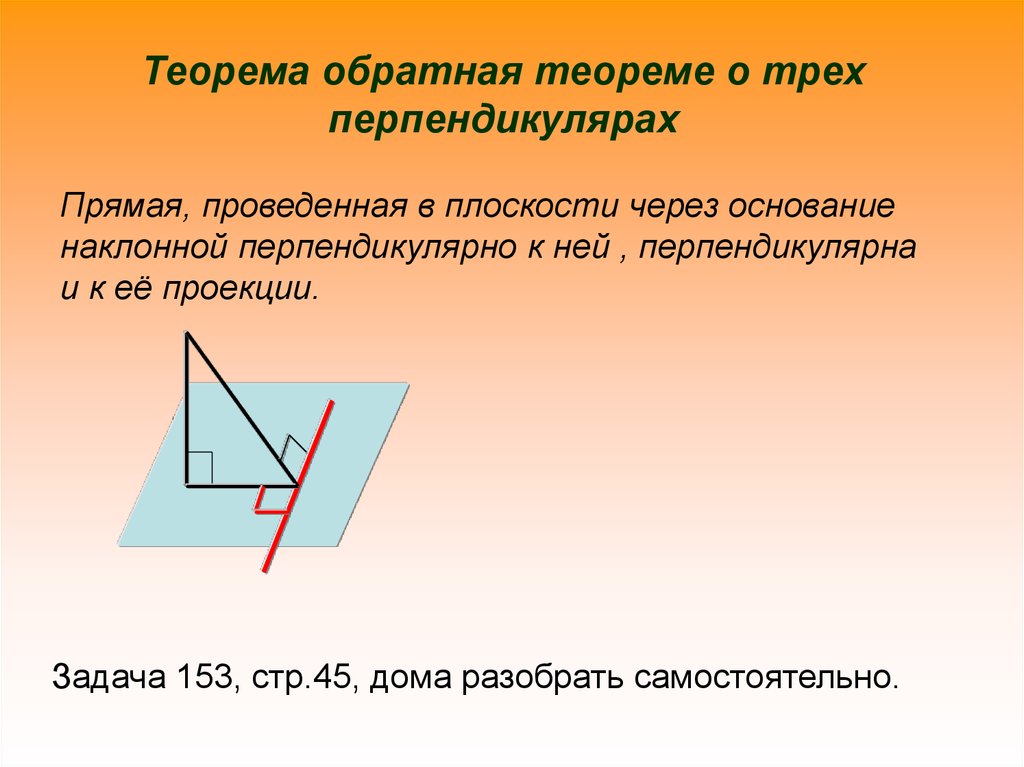
Изучите исторические аспекты возникновения теоремы, чтобы лучше понять её значимость и применение в современной геометрии.

Проверьте свои знания, участвуя в математических конкурсах и олимпиадах, где задачи на стереометрию часто включают использование теоремы о трех перпендикулярах.