Синус угла между прямой и плоскостью: полезные советы
Синус угла между прямой и плоскостью в пространстве - это важная тема в геометрии, которая находит применение в различных областях науки и техники. В этом материале вы найдете полезные советы и наглядные примеры для лучшего понимания.


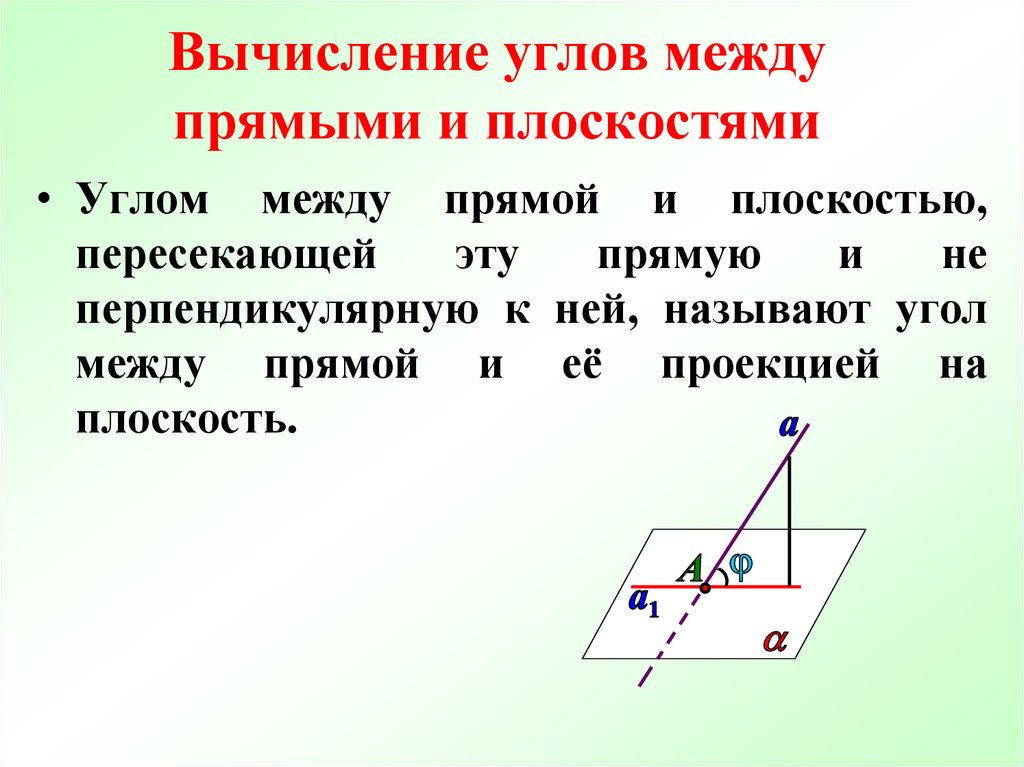
Для вычисления синуса угла между прямой и плоскостью, сначала найдите вектор нормали к плоскости.
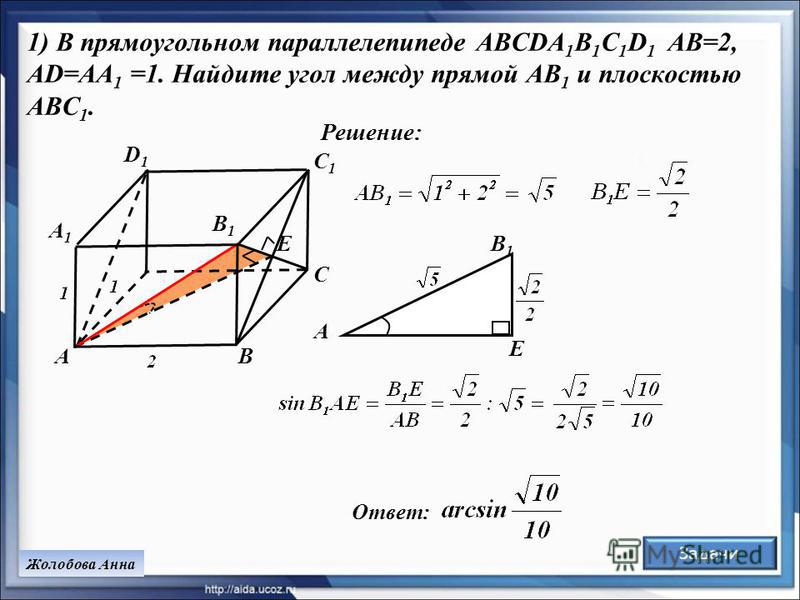
Используйте векторное произведение для нахождения нормали к плоскости, если у вас есть три точки на плоскости.
10 класс, 21 урок, Угол между прямой и плоскостью
Нормализуйте векторы, чтобы упростить вычисления синуса угла между прямой и плоскостью.
Видеоурок \
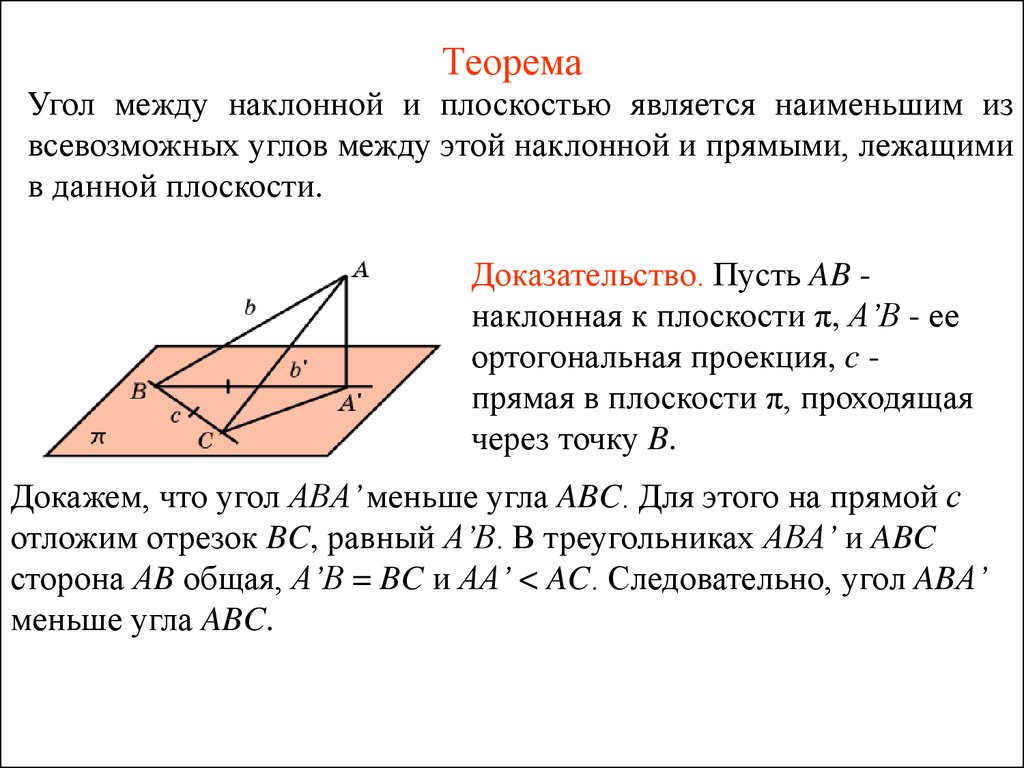
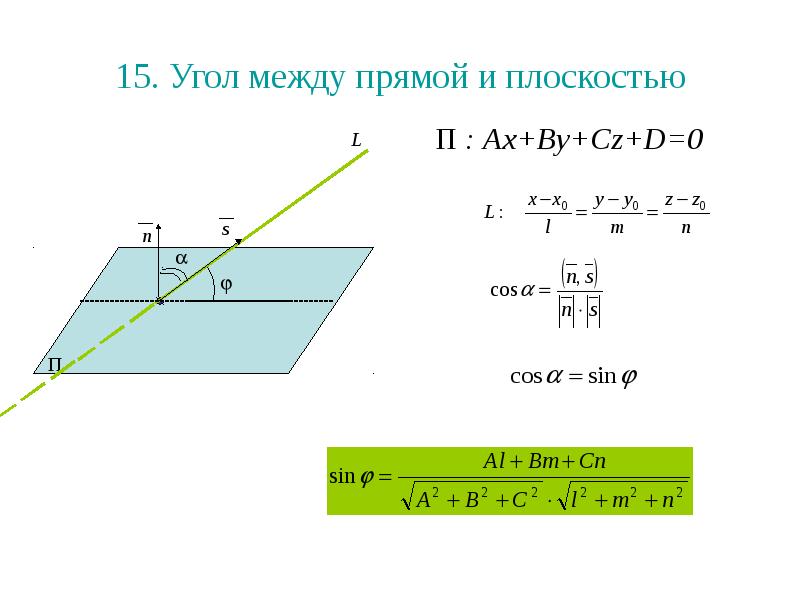
Используйте скалярное произведение для нахождения косинуса угла между направляющим вектором прямой и нормалью плоскости.
Помните, что синус угла можно найти через косинус с помощью основного тригонометрического тождества.


Внимательно проверяйте все вычисления, чтобы избежать ошибок в итоговом значении синуса угла.
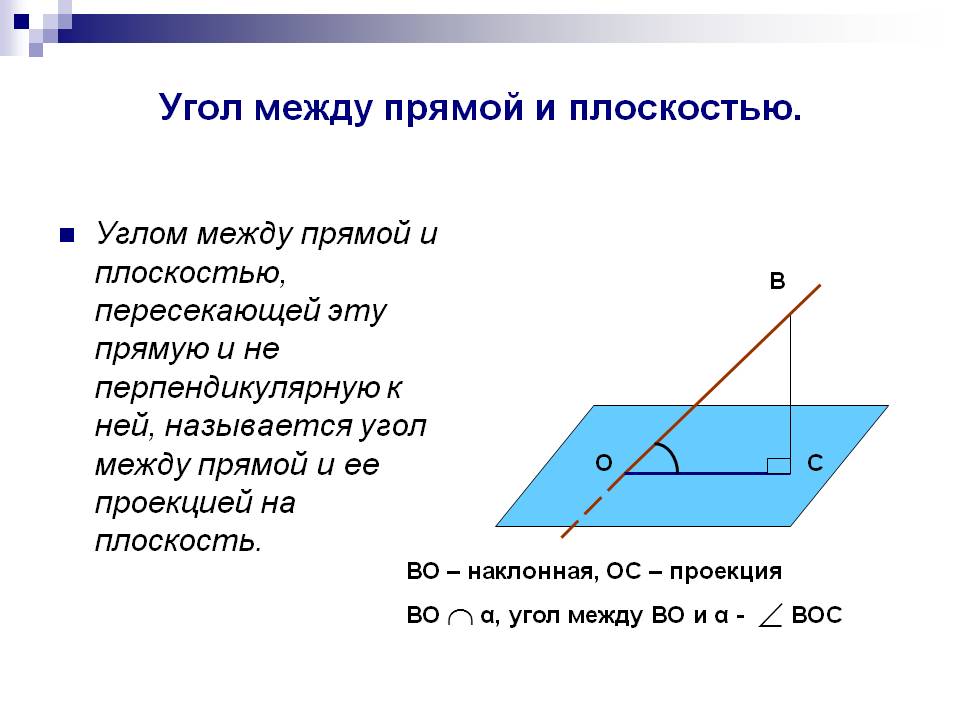
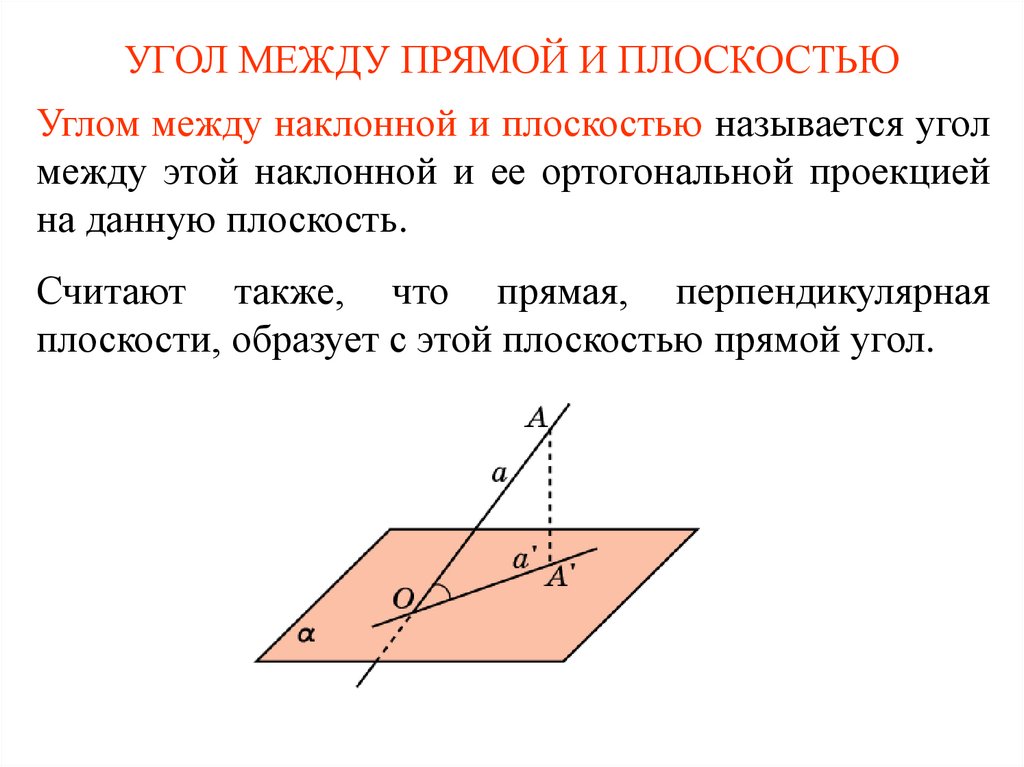
Пользуйтесь программными средствами, такими как MATLAB или GeoGebra, для визуализации и проверки ваших расчетов.

Для сложных задач разбивайте их на более простые шаги и решайте их последовательно.
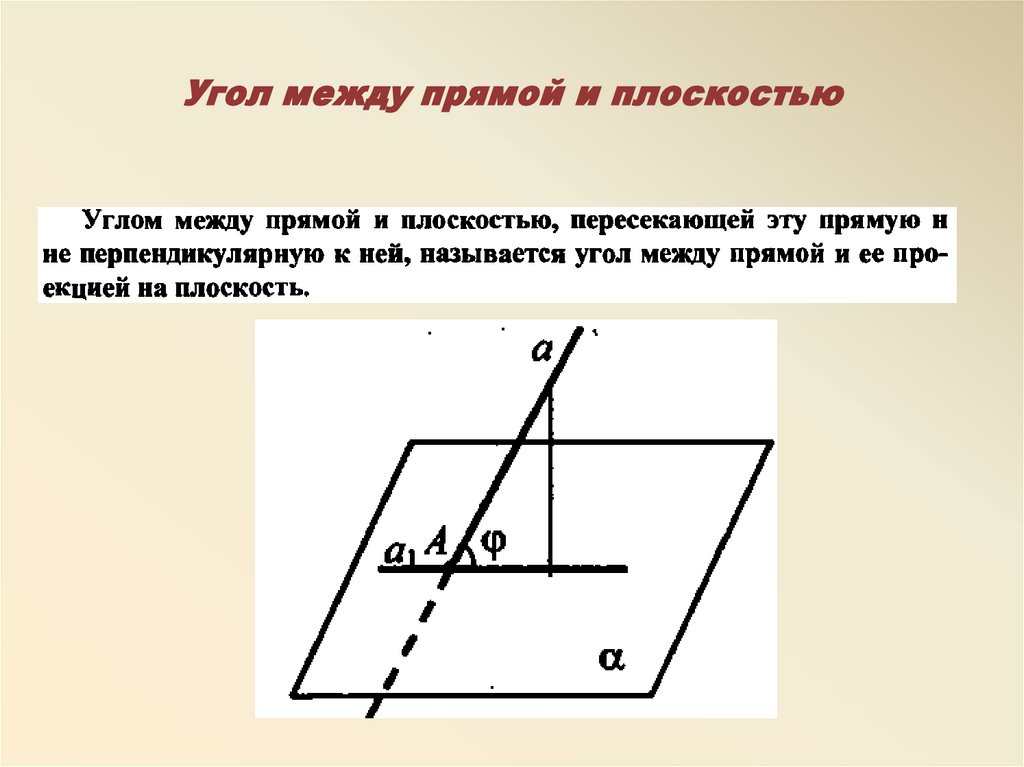
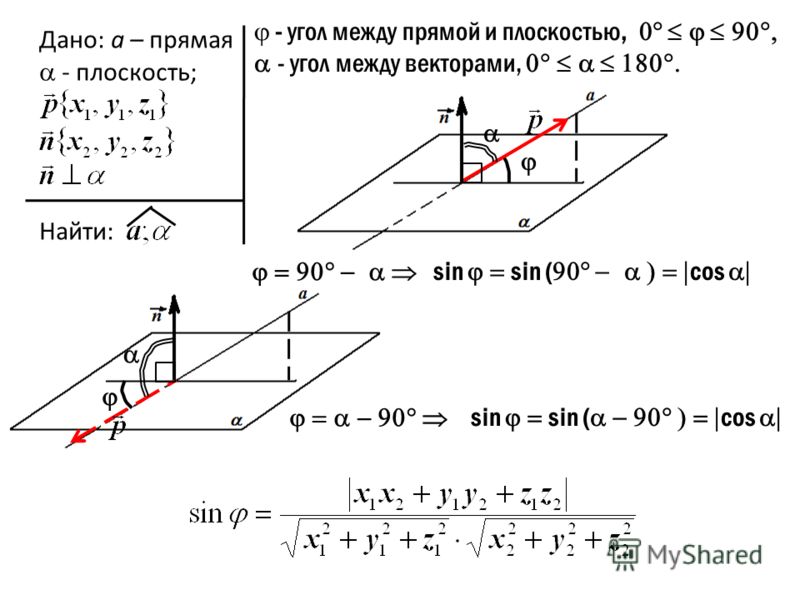
Изучите примеры решений аналогичных задач в учебниках по аналитической геометрии.

Практикуйтесь регулярно, решая разнообразные задачи, чтобы лучше освоить методы вычисления синусов углов между прямыми и плоскостями.