Изучаем свойства четырехугольников, вписанных в окружность: полное руководство
Четырехугольники, вписанные в окружность, имеют уникальные геометрические свойства, которые отличают их от других четырехугольников. В этой статье мы рассмотрим ключевые свойства таких четырехугольников и предложим полезные советы для их изучения и применения.
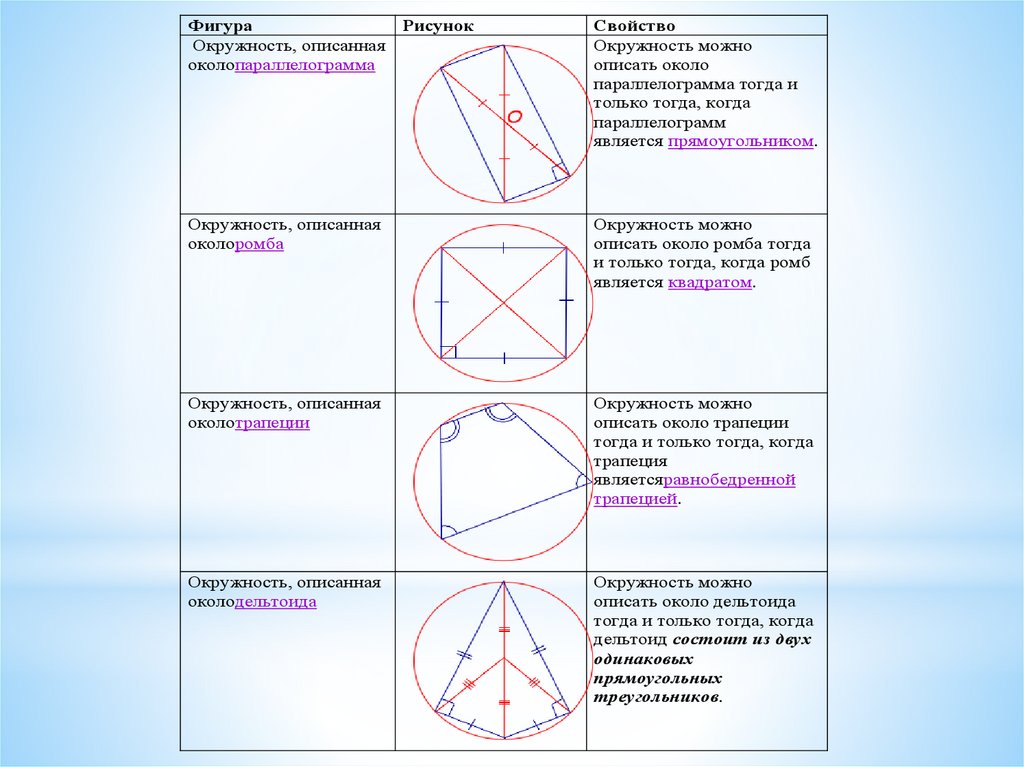


Проверяйте, что все углы четырехугольника, вписанного в окружность, суммируются в 360 градусов.
#Свойство углов вписанного четырехугольника
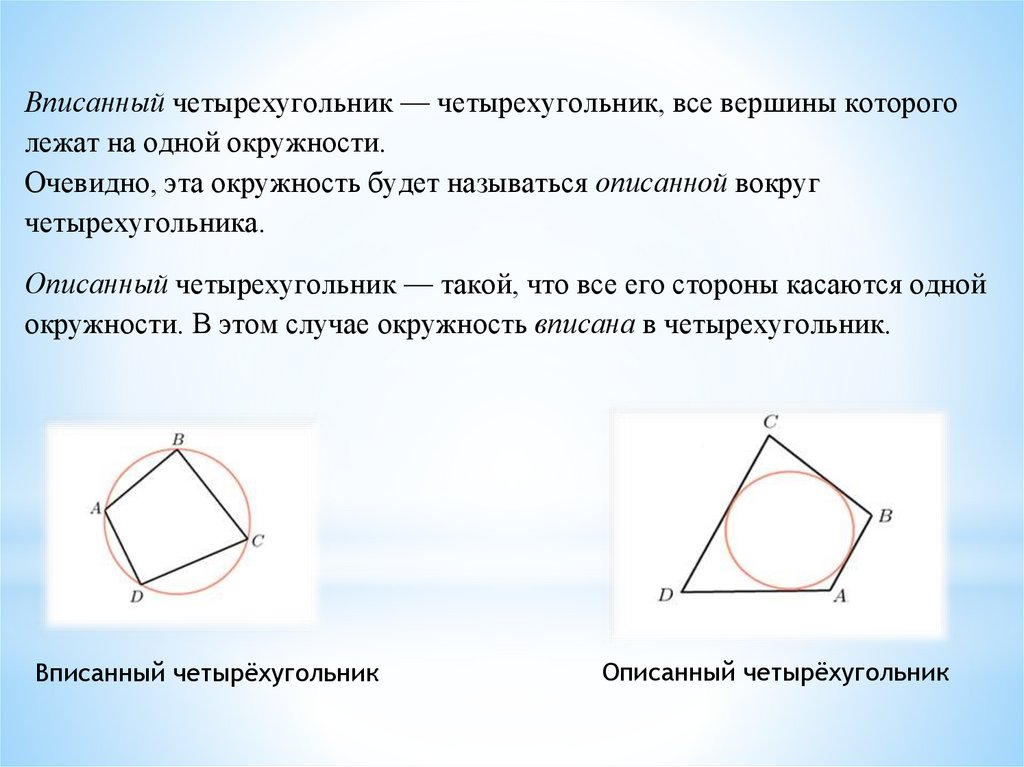
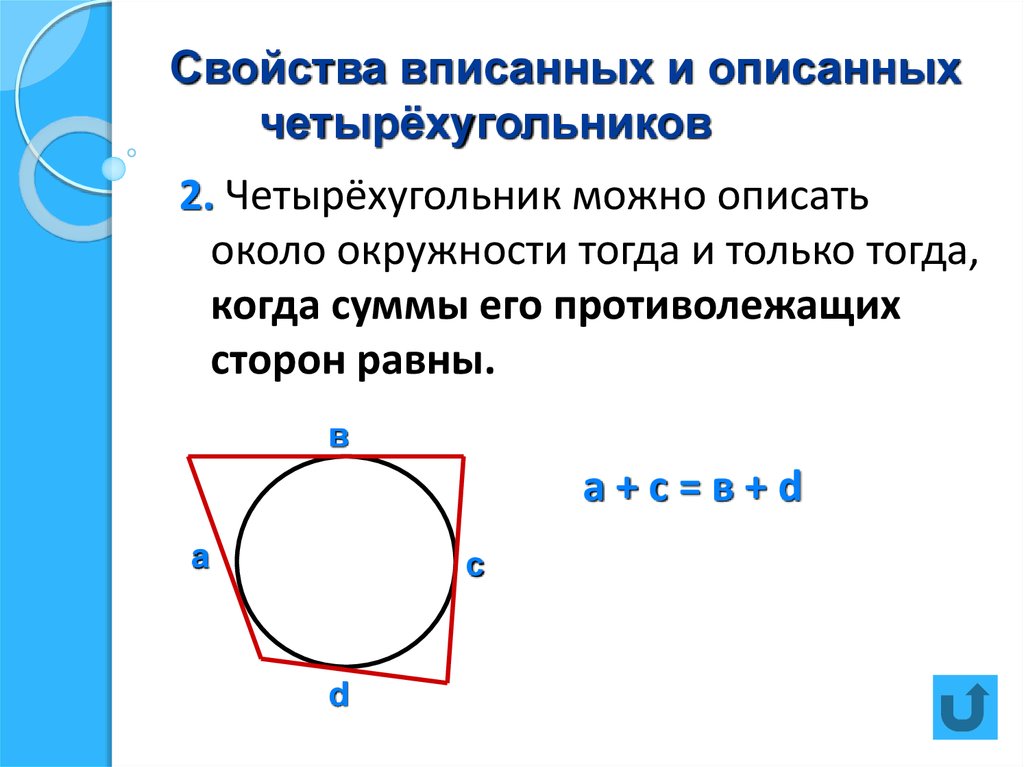
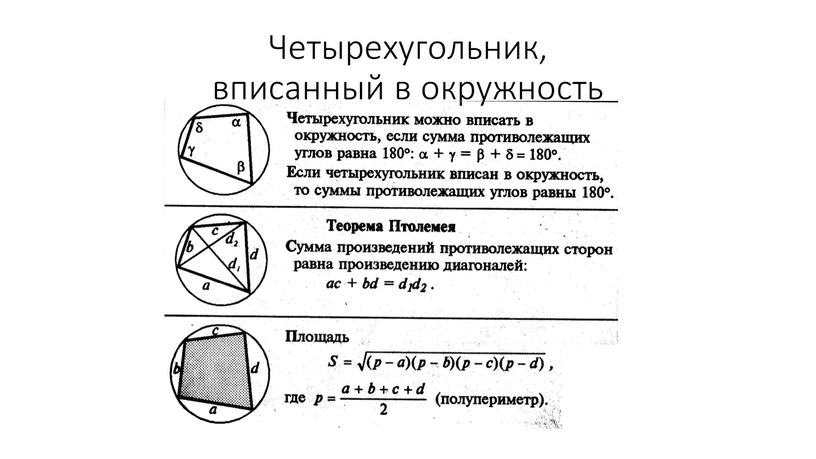
Используйте теорему Птолемея для решения задач, связанных с такими четырехугольниками.
8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4
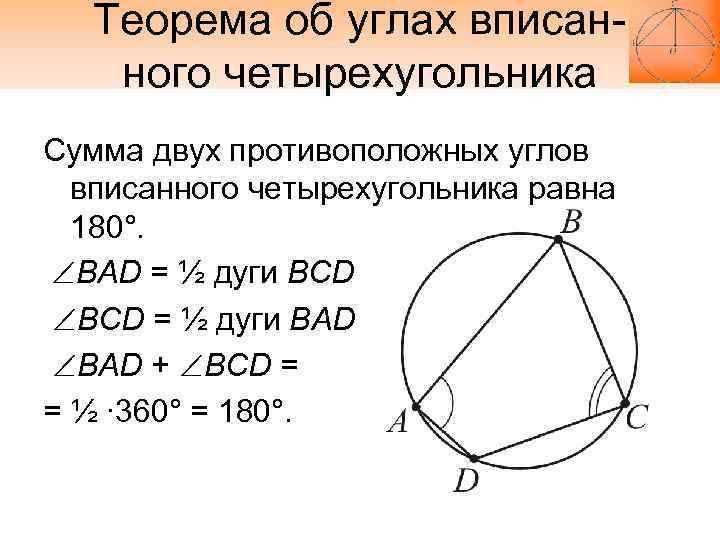

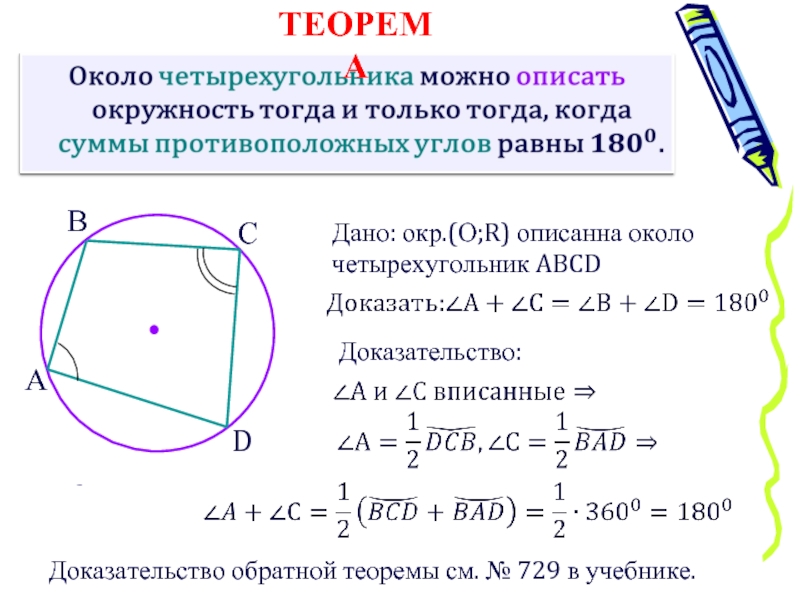
Помните, что сумма противоположных углов в таком четырехугольнике всегда равна 180 градусам.
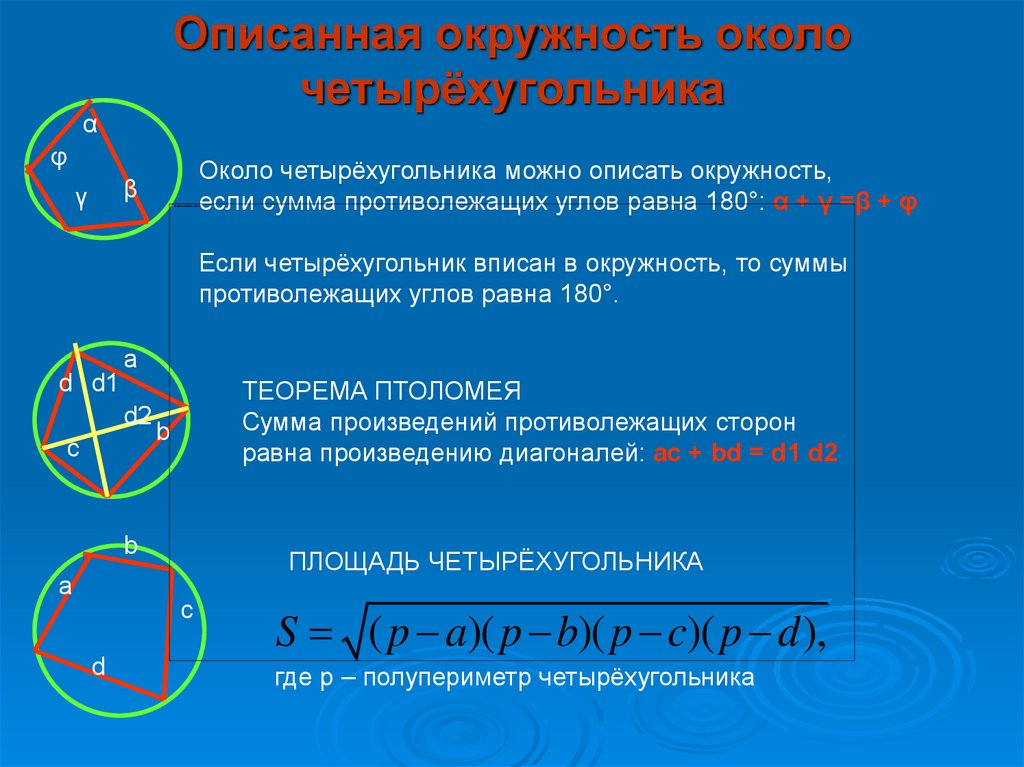
Используйте свойство, что диагонали вписанного четырехугольника пересекаются в точке, и их произведение пропорционально произведению отрезков на этих диагоналях.
Разбирайте практические примеры, чтобы лучше понять применение свойств вписанных четырехугольников.

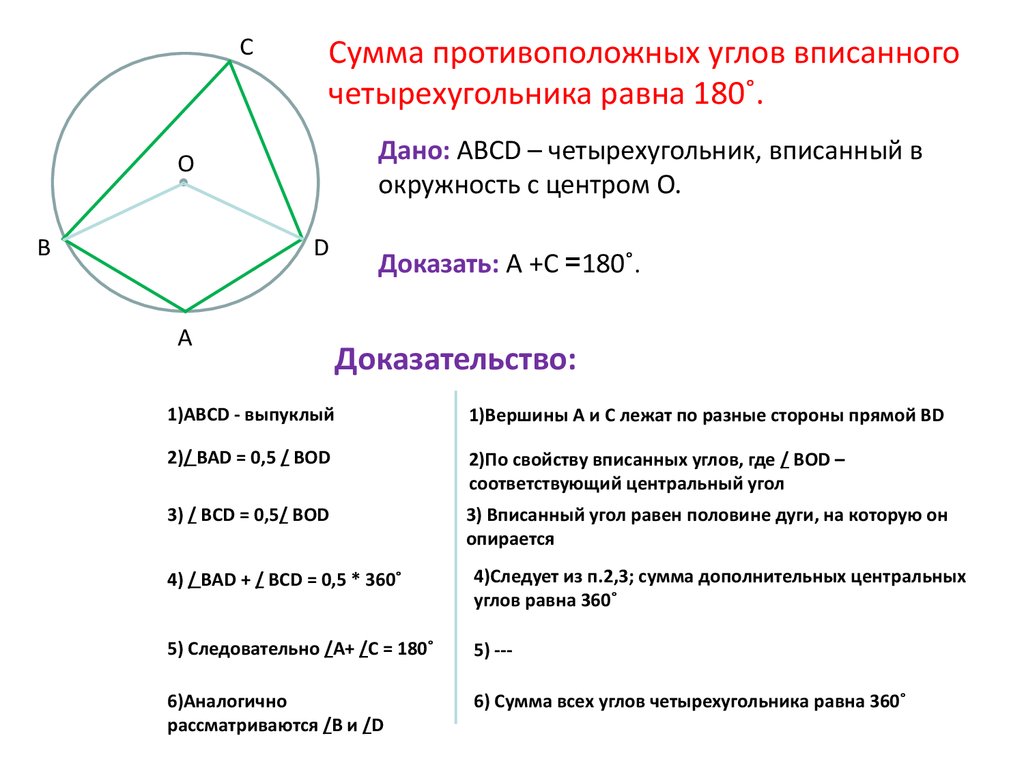
При решении задач с вписанными четырехугольниками всегда проверяйте, что точки действительно лежат на одной окружности.
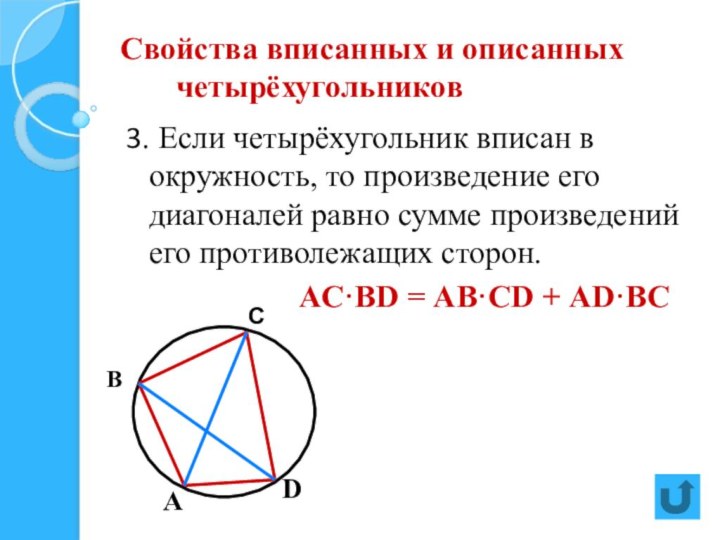
Используйте геометрические чертежи для визуализации и подтверждения свойств четырехугольников.

Ознакомьтесь с различными методами доказательства свойств вписанных четырехугольников, чтобы расширить свои знания.
Работайте с конкретными примерами и задачами для лучшего понимания применения теоретических знаний.
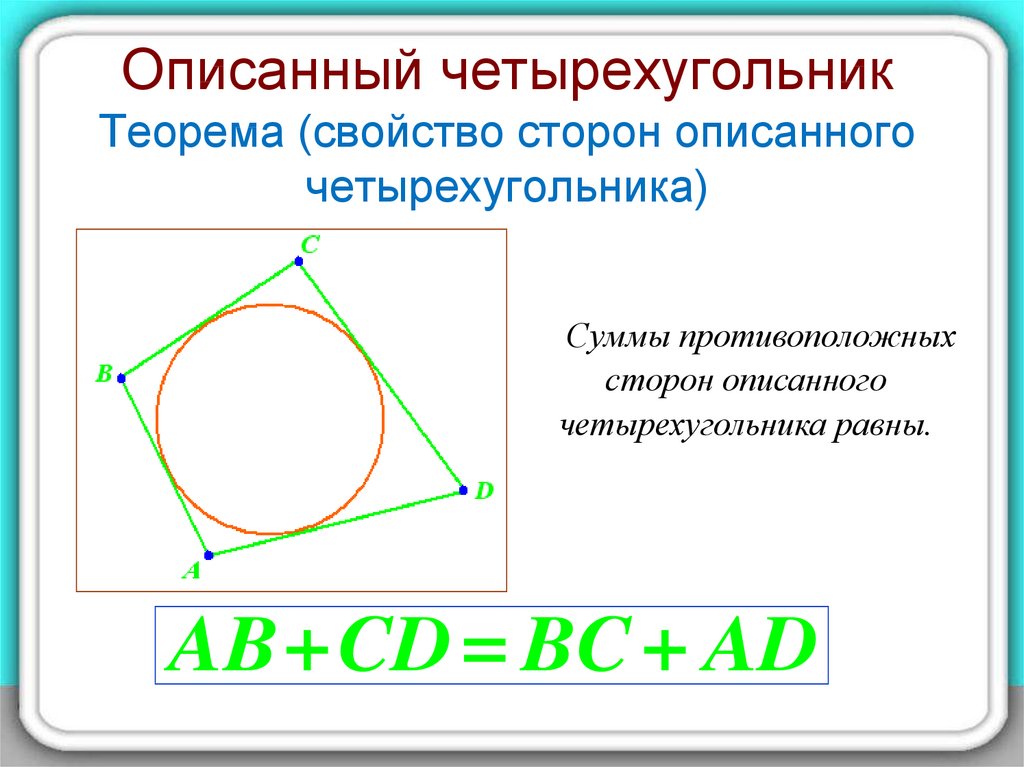
Уроки геометрии. Одно замечательное свойство четырехугольника, описанного вокруг окружности.
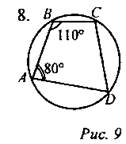
Обратите внимание на возможные ошибки при построении и расчетах, чтобы избежать распространенных проблем.