Методы создания и анализа треугольников ABC и A1B1C1
Эта страница посвящена методам построения треугольников ABC и A1B1C1, а также полезным советам по их сравнению и анализу. Вы найдете здесь фотографии и инструкции, которые помогут вам лучше понять геометрические свойства этих фигур.
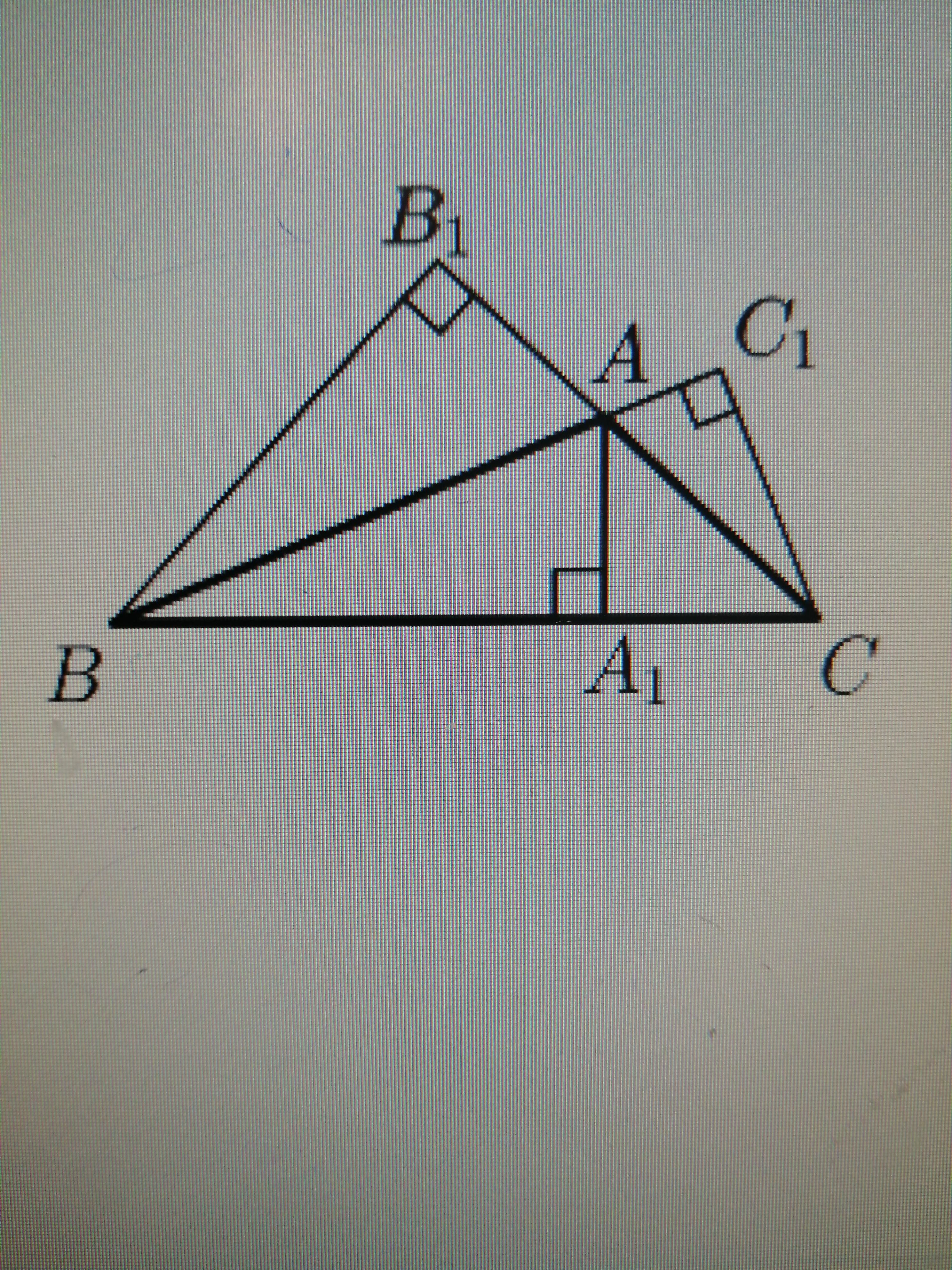


Для начала определите координаты всех вершин треугольников на плоскости.
№545. Треугольники ABC и А1В1С1 подобны, и их сходственные стороны относятся как 6:5
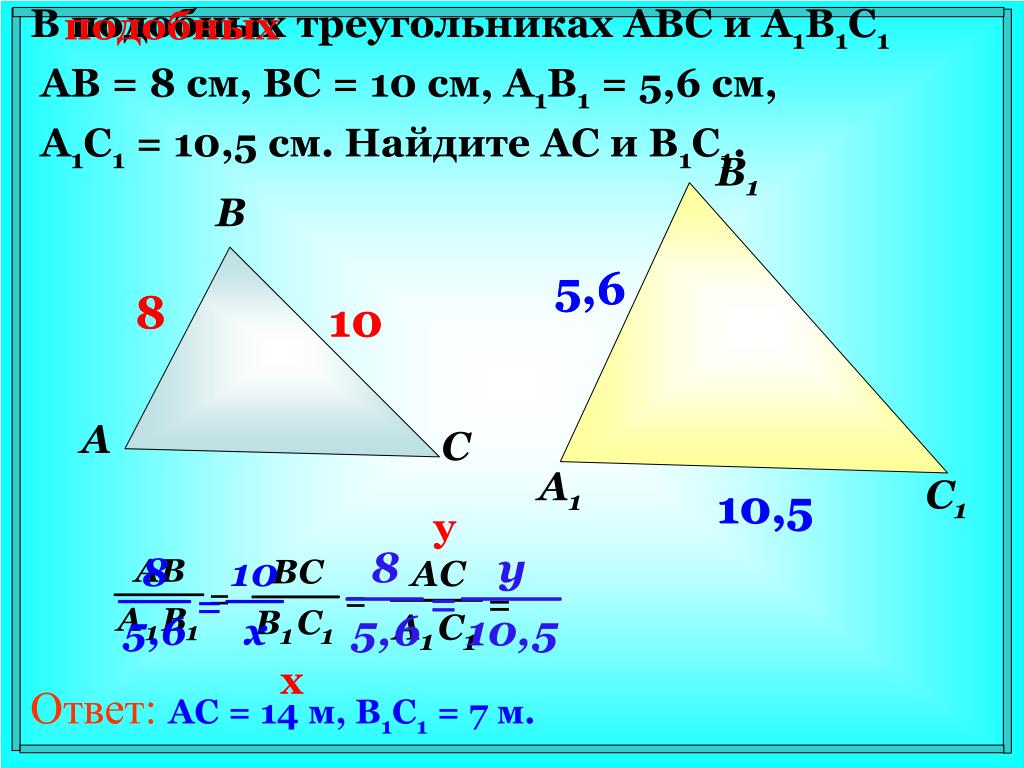
Используйте линейку и транспортир для точного построения треугольников на бумаге.
№269. Докажите, что ΔАВС=ΔА1B1С1, если ∠A=∠A1, ∠B=∠B1 и ВН=В1Н1, где ВН и В1Н1


Примените теорему Пифагора для проверки равенства сторон треугольников.
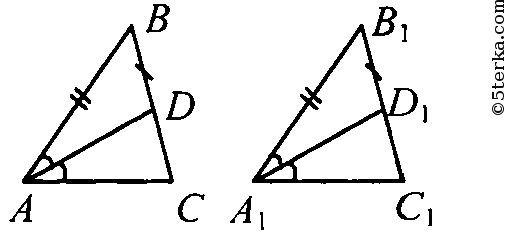
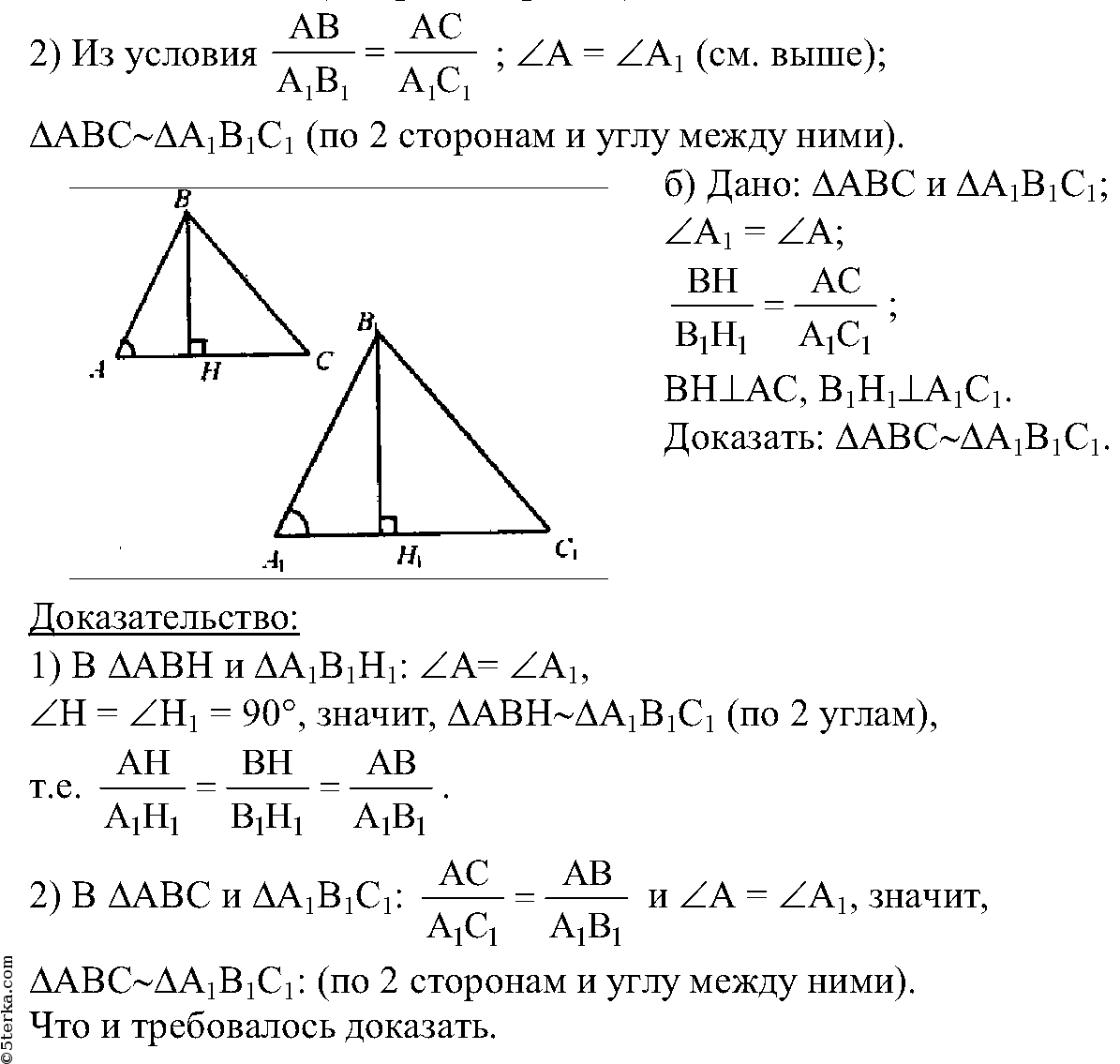
Используйте программу для геометрических построений, например, GeoGebra, для более точных расчетов.
Геометрия В треугольниках ABC и A1B1C1 известно, что угол A = углу A1, каждая из сторон AB и AC

Проверьте равенство углов треугольников с помощью транспортирующих приборов.
№177* Даны два треугольника: ABC и А1В1С1. Известно, что АВ=А1В1, АС=А1С1, ∠A=∠A1. На сторонах АС
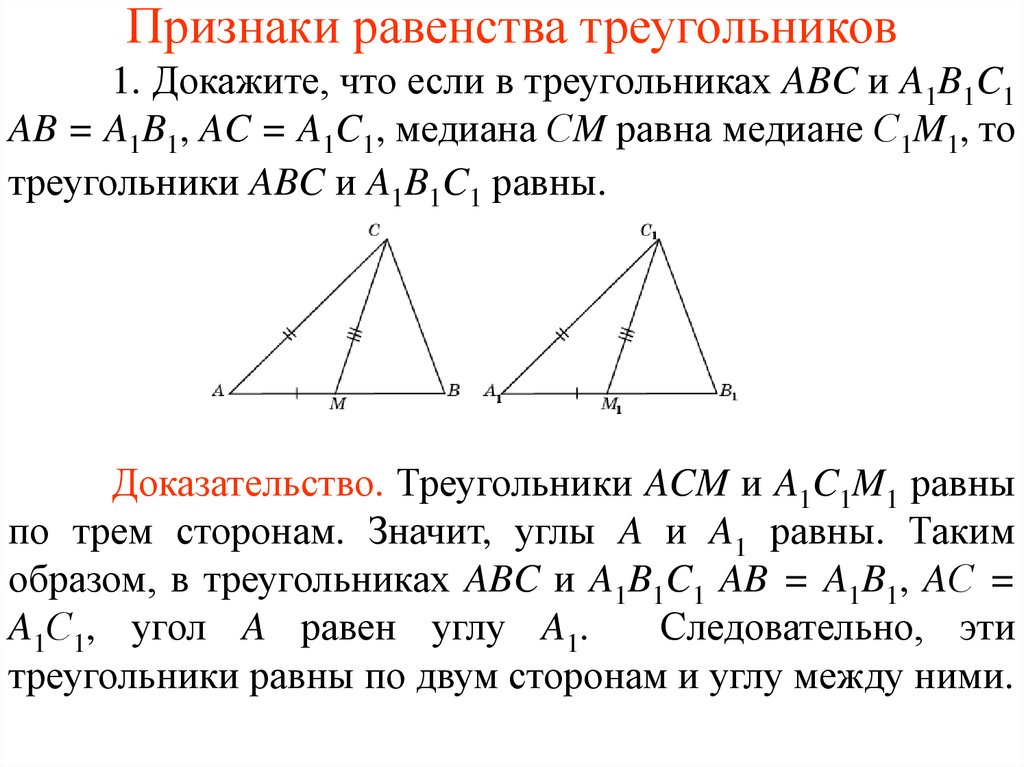
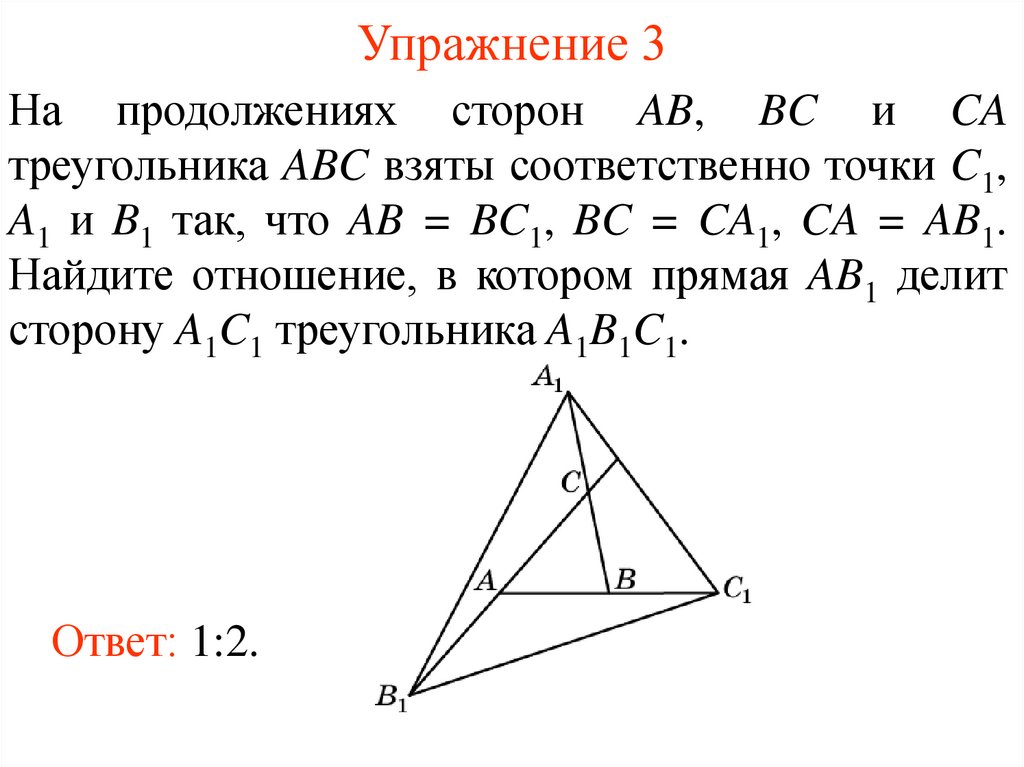
Изучите свойства медиан, биссектрис и высот для каждого треугольника.
Используйте таблицы и формулы для расчета площадей треугольников.

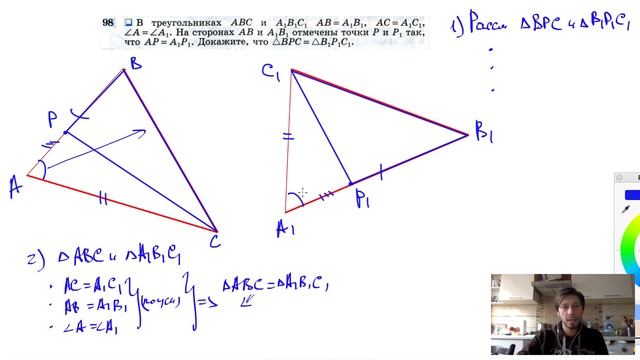
Сравните периметры треугольников, чтобы определить их сходство и различие.
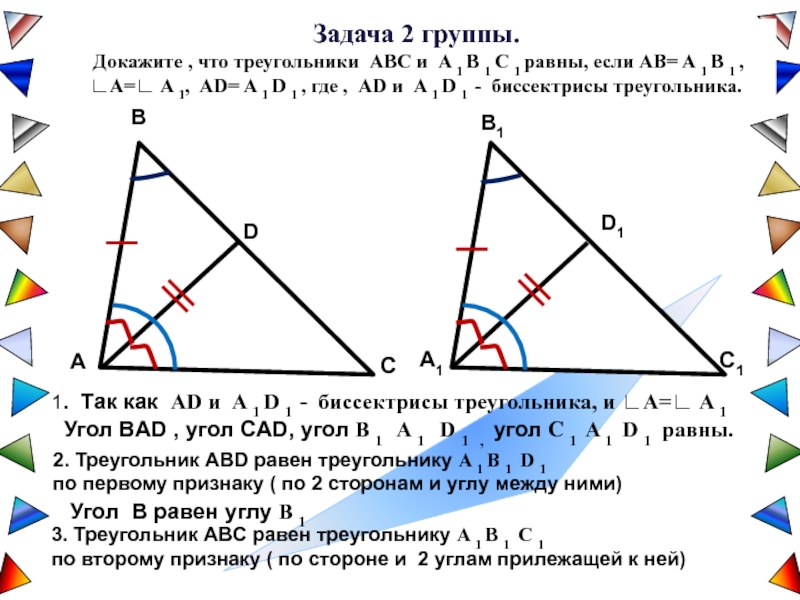
Обратите внимание на симметричные свойства треугольников.
Только 1% может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬ
Для более сложных задач используйте тригонометрические функции для проверки соответствия углов и сторон треугольников.