Понимание центральных и вписанных углов: советы и примеры
В этой подборке вы найдете полезные советы и изображения, которые помогут вам понять и правильно использовать концепции центральных и вписанных углов в различных графических и математических задачах. Мы рассмотрим, как эти углы применяются в рисунках, диаграммах и других визуальных материалах.

Для точного изображения углов используйте циркуль и транспортир для измерения и черчения.
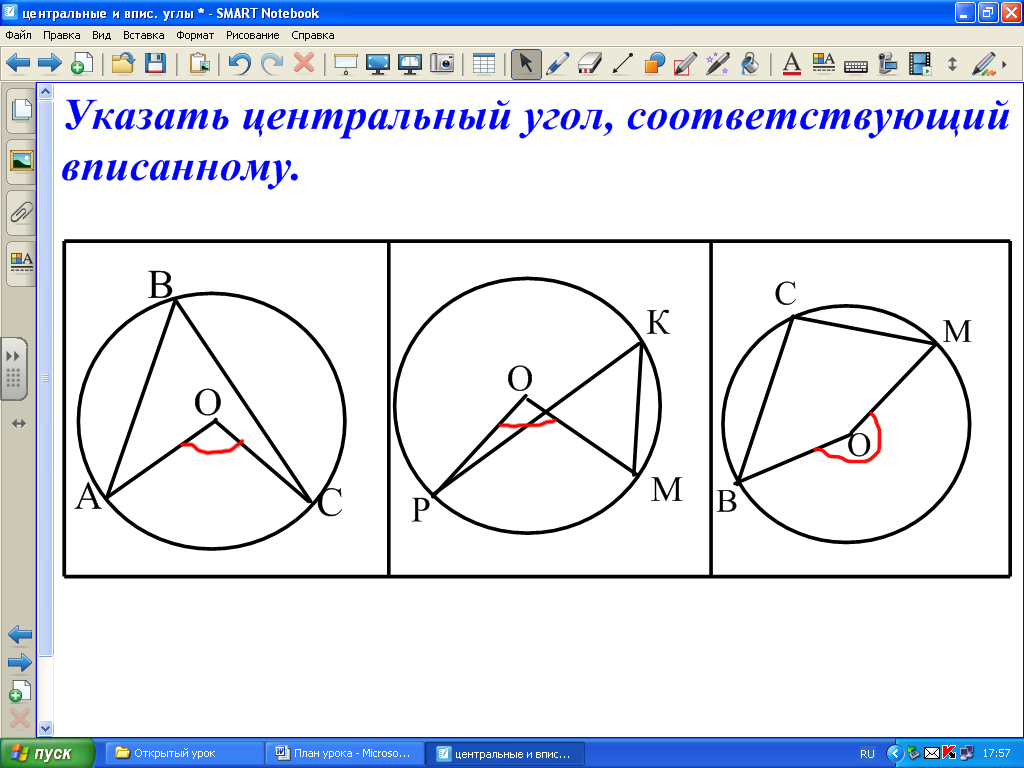
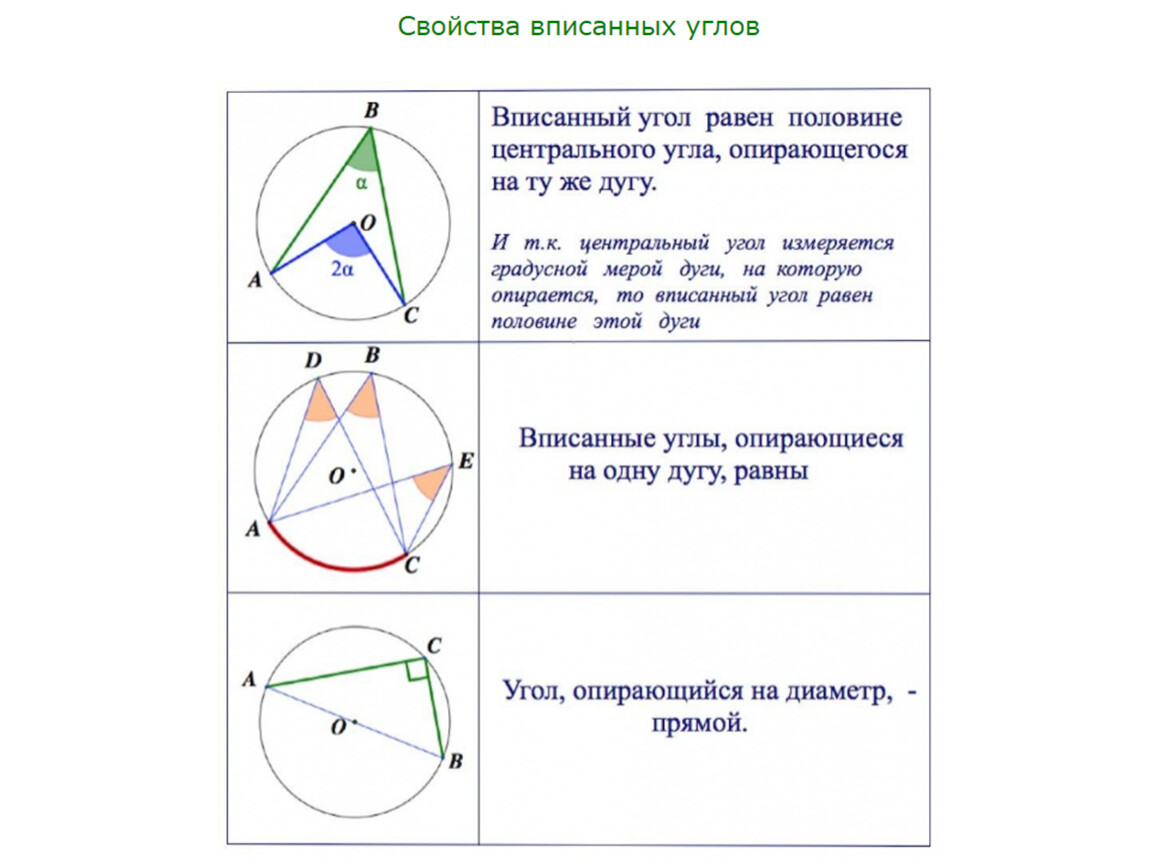
Центральный угол можно определить как угол, вершина которого находится в центре окружности.
Геометрия. Тестовая часть. Урок 1. Центральные и вписанные углы, Вписанная и описанная окружность
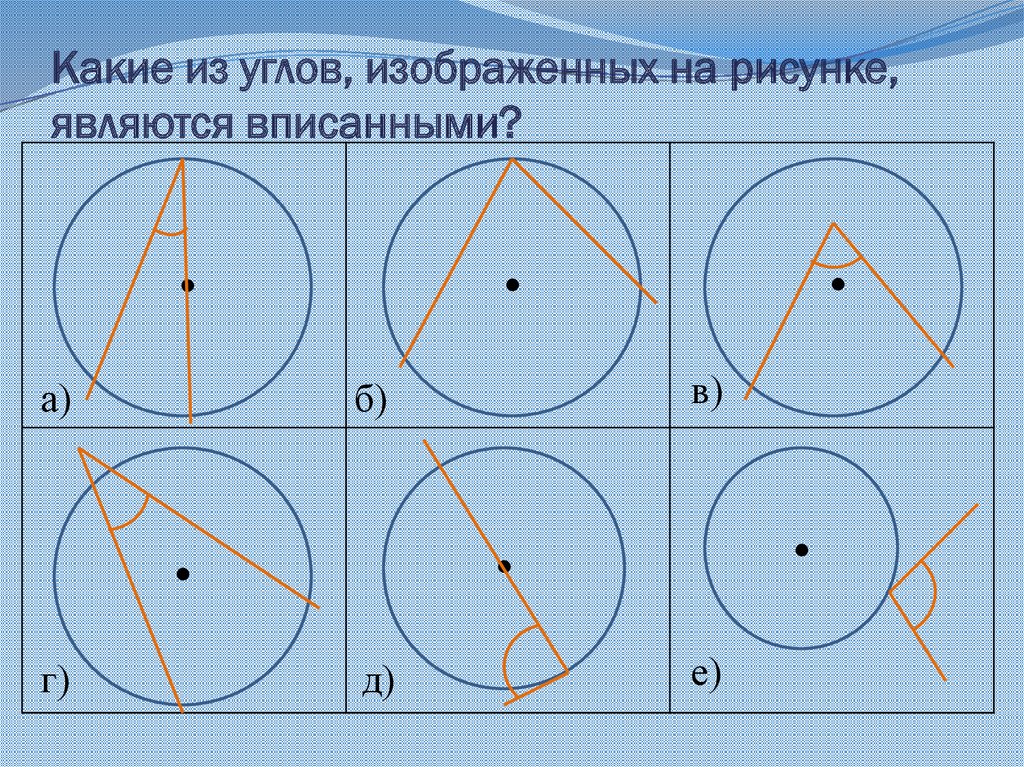

Вписанный угол равен половине центрального угла, который опирается на ту же дугу окружности.
Центральные и вписанные углы. Всё про углы в окружности


Используйте цветные маркеры для выделения углов в рисунках, чтобы облегчить понимание их взаимосвязи.
Как понять центральные и вписанные углы
При работе с диаграммами старайтесь поддерживать единый масштаб, чтобы углы были пропорциональны.
ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный Угол

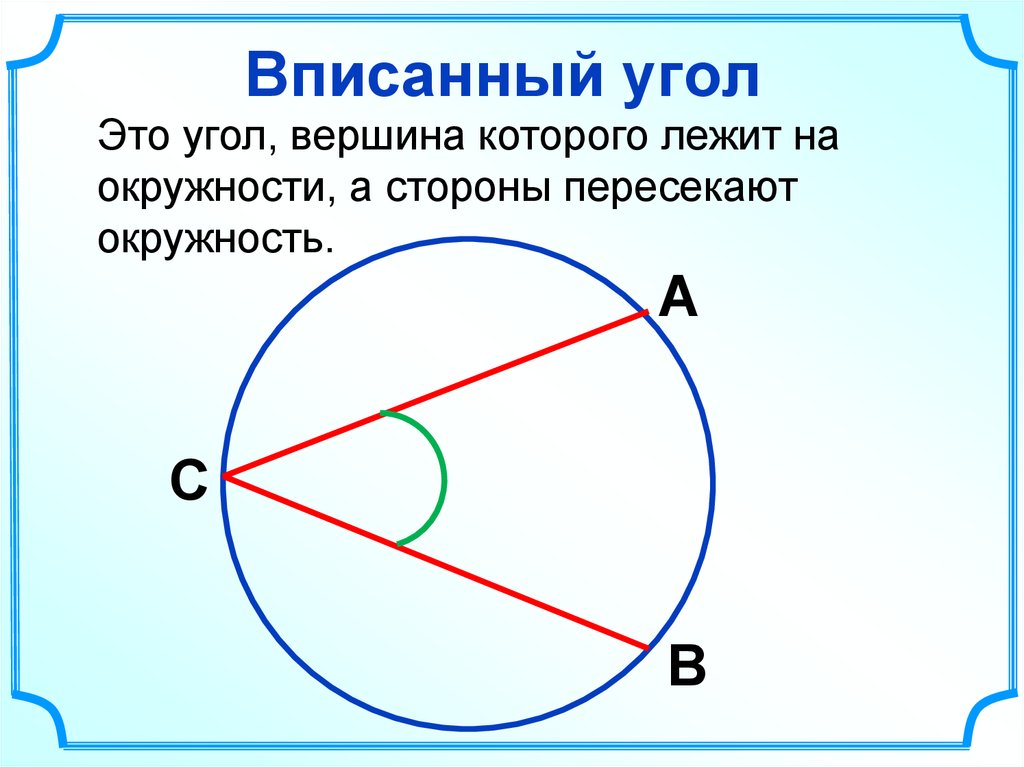
В рисунках, где требуется точность, проверяйте углы с помощью программного обеспечения для черчения.

Не забывайте, что вписанные углы всегда будут меньшими по величине по сравнению с центральными углами.
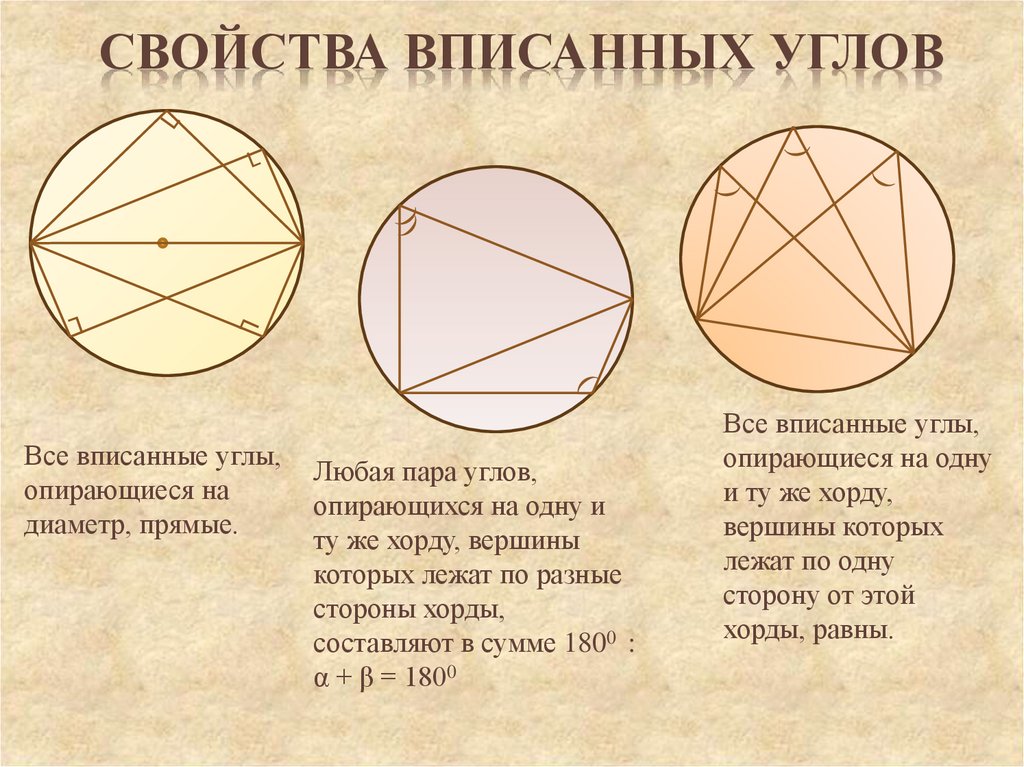

Для сложных диаграмм используйте сетку или направляющие линии, чтобы углы отображались более точно.
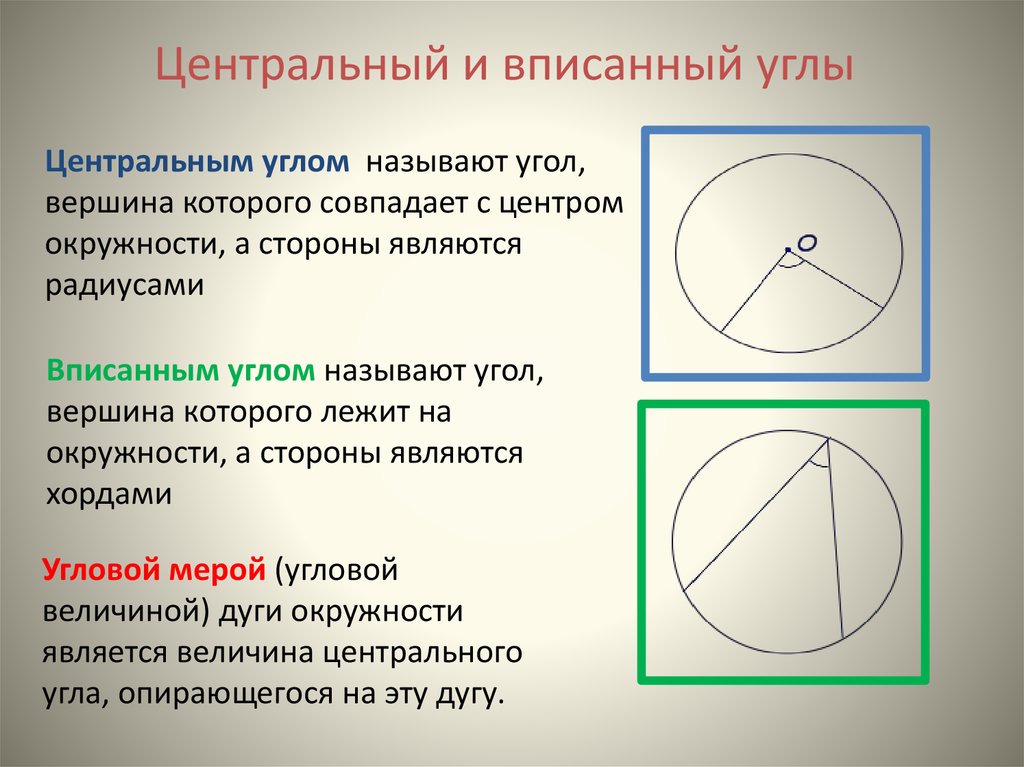
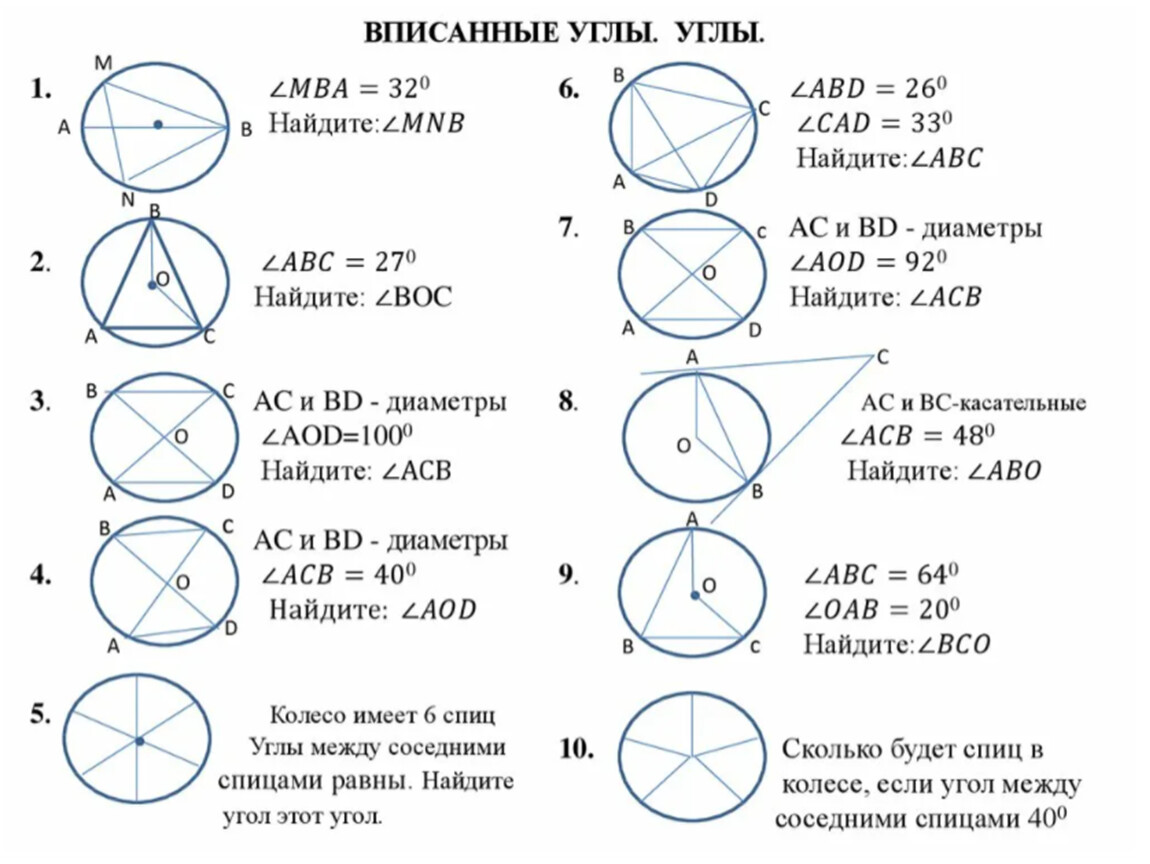
Периодически проверяйте измерения и корректность углов, чтобы избежать ошибок в работе.
Углы, вписанные в окружность. 9 класс.
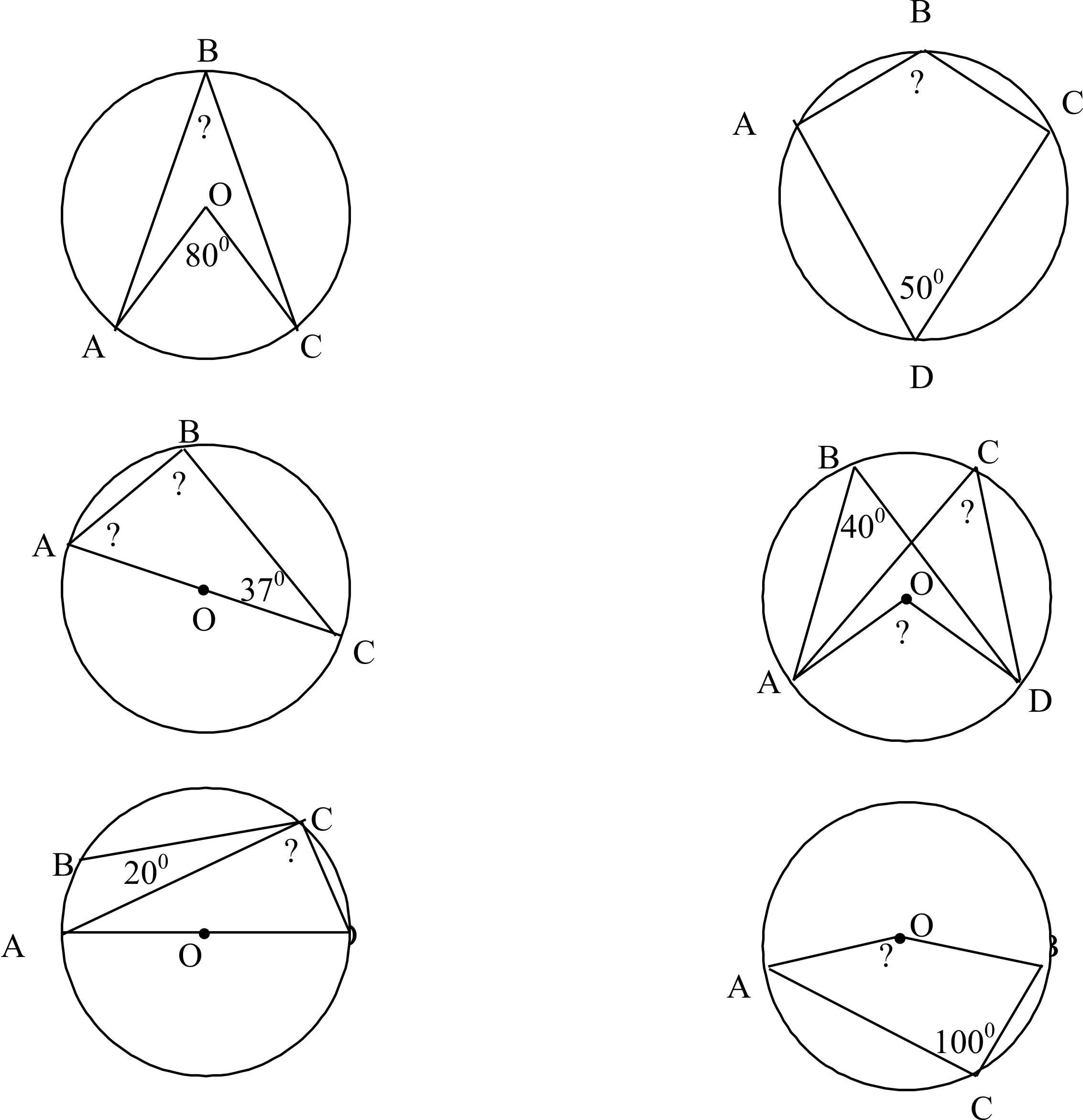

Знайте, что понимание центральных и вписанных углов важно не только в геометрии, но и в других областях, таких как инженерия и архитектура.