Основы коллинеарности векторов: что нужно знать

Коллинеарность векторов — это важное понятие в математике и физике. Векторы считаются коллинеарными, если они лежат на одной прямой или параллельны друг другу. В этом руководстве вы найдете полезные советы и методы определения коллинеарности векторов, что поможет вам лучше понять и применять этот концепт в различных задачах.

Для проверки коллинеарности двух векторов вычислите их скалярное произведение. Если результат равен нулю, векторы перпендикулярны, но это не исключает их коллинеарности.

Используйте координатный метод: два вектора (a, b) и (c, d) коллинеарны, если отношение их соответствующих координат одинаково, то есть a/c = b/d.

Векторы можно считать коллинеарными, если один из них является линейной комбинацией другого. Проверьте это, выразив один вектор через коэффициенты другого.

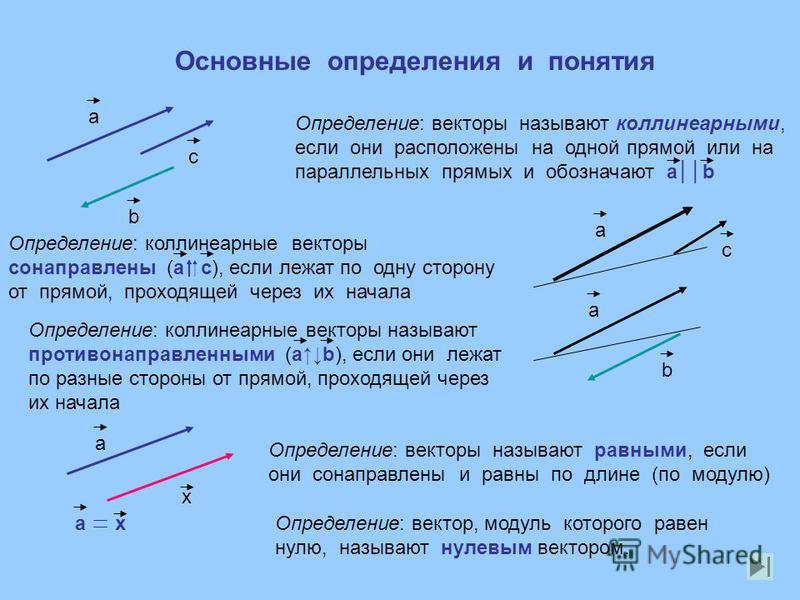
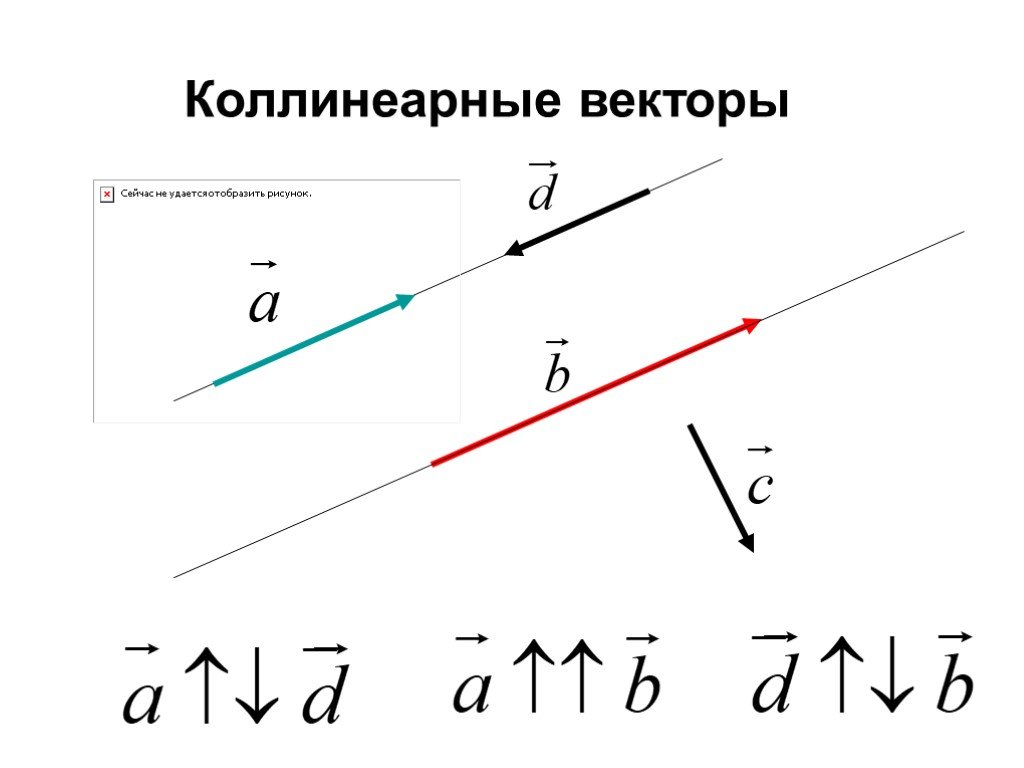
Графически векторы можно проверить на коллинеарность, если они лежат на одной прямой или параллельны друг другу.

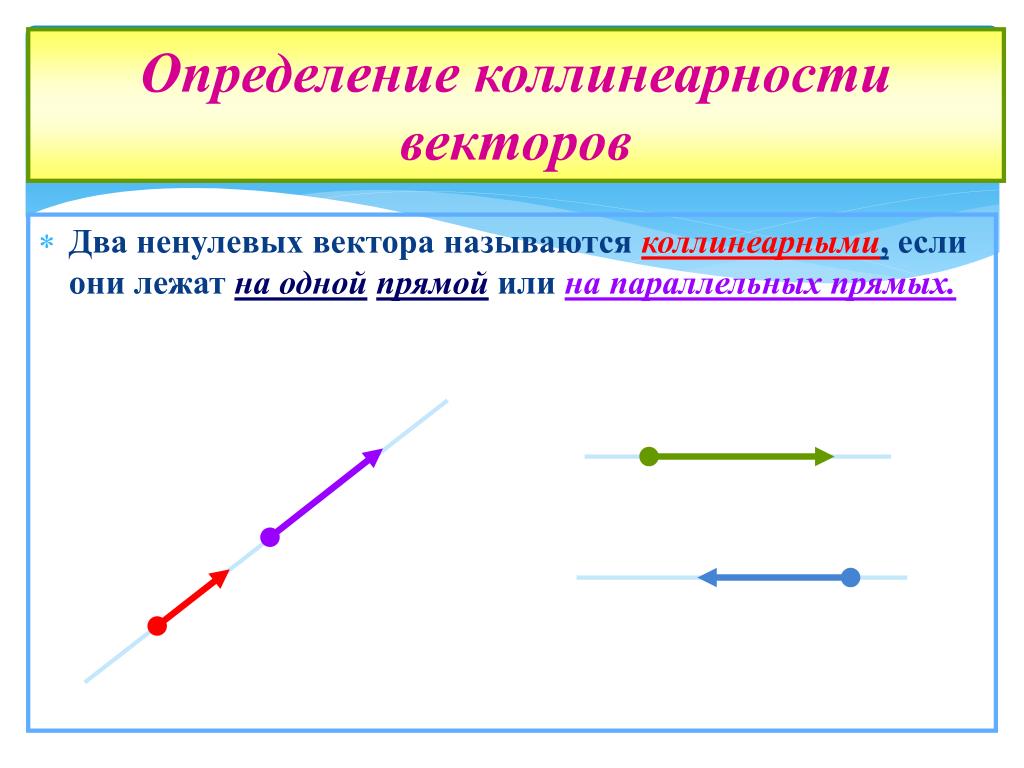
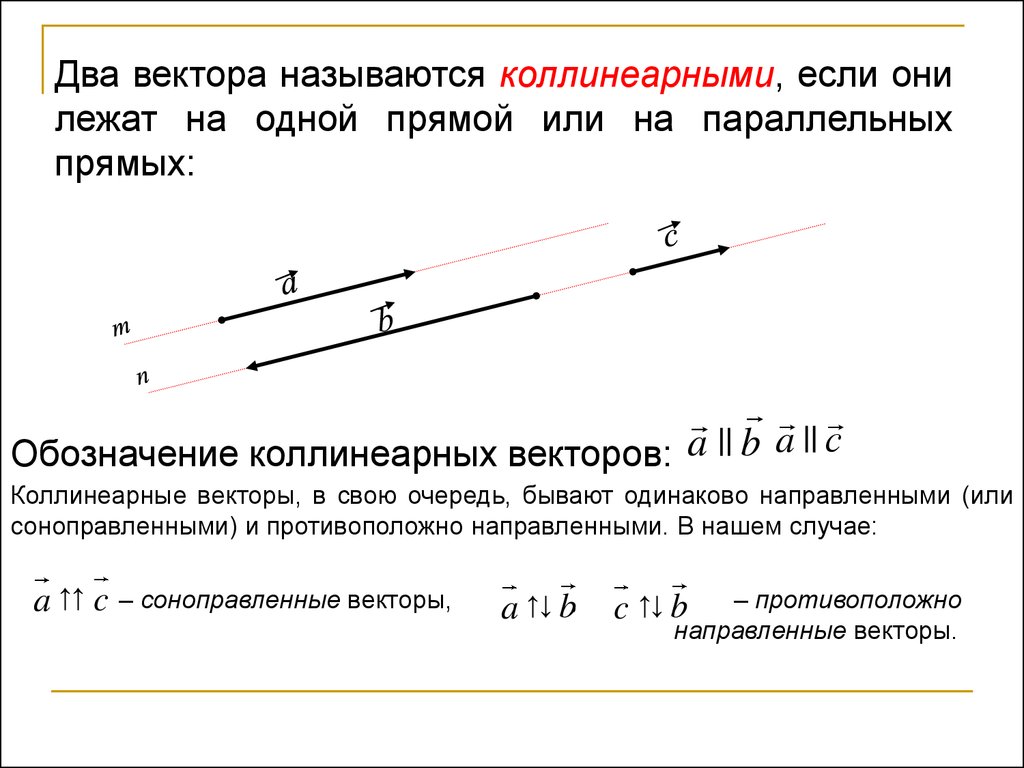
Если вам необходимо проверить коллинеарность векторов в 3D-пространстве, используйте метод векторного произведения. Если результат равен нулю, векторы коллинеарны.

Обратите внимание на единичные векторы: если два вектора коллинеарны, то их единичные векторы будут параллельны.

При работе с векторами в различных системах координат используйте преобразования, чтобы проверить их коллинеарность в одной и той же системе.

Используйте геометрическое представление векторов на плоскости или в пространстве для визуальной проверки их коллинеарности.

Проверьте, являются ли векторы кратными друг другу. Если один вектор является скалярным произведением другого, они коллинеарны.

Для комплексных чисел проверьте их аргументы. Векторы коллинеарны, если их углы между осью X одинаковы.