Как найти вершины гиперболы с помощью формул

Гипербола — это важная кривая в математике, часто встречающаяся в различных научных и инженерных областях. Вершины гиперболы играют ключевую роль в её характеристиках и применениях. В этом разделе мы рассмотрим, как найти и использовать формулы для определения вершин гиперболы, а также предоставим полезные советы по визуализации и применению этих знаний.

Начните с определения уравнения гиперболы в стандартной форме.

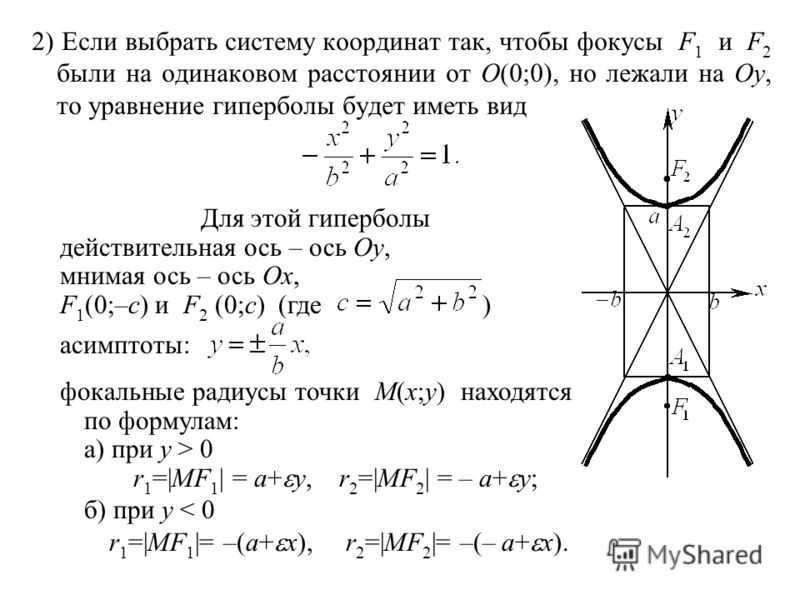
Определите центр гиперболы для дальнейшего расчета вершин.

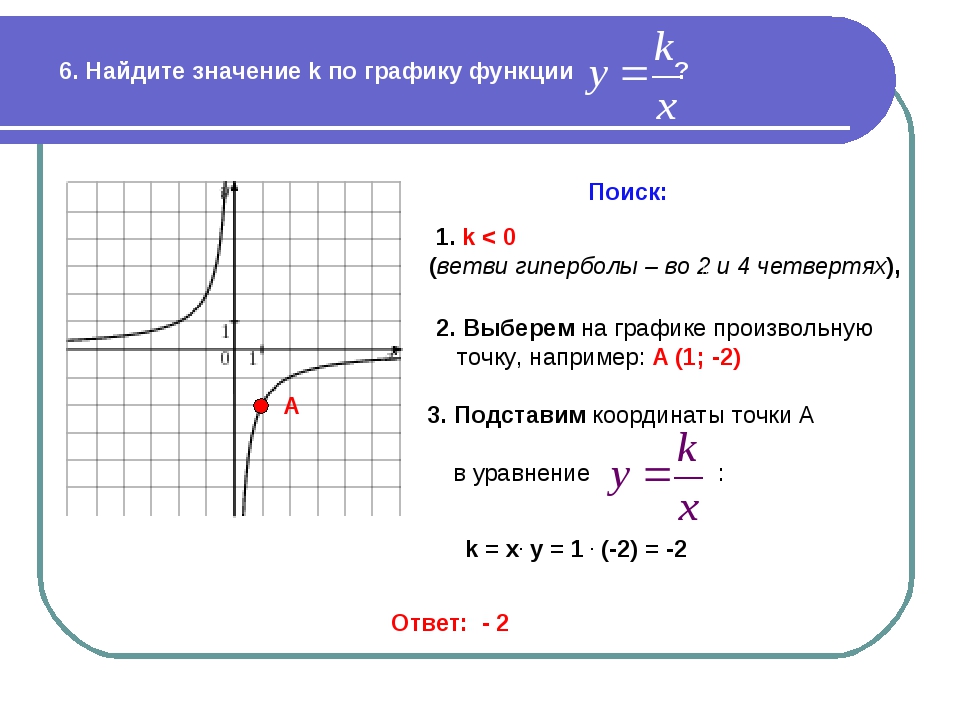
Используйте формулы для вычисления расстояния от центра до вершины.

Проверьте знаки в уравнении, чтобы определить ориентацию гиперболы.

Если гипербола горизонтальная, вершины будут расположены по оси X.

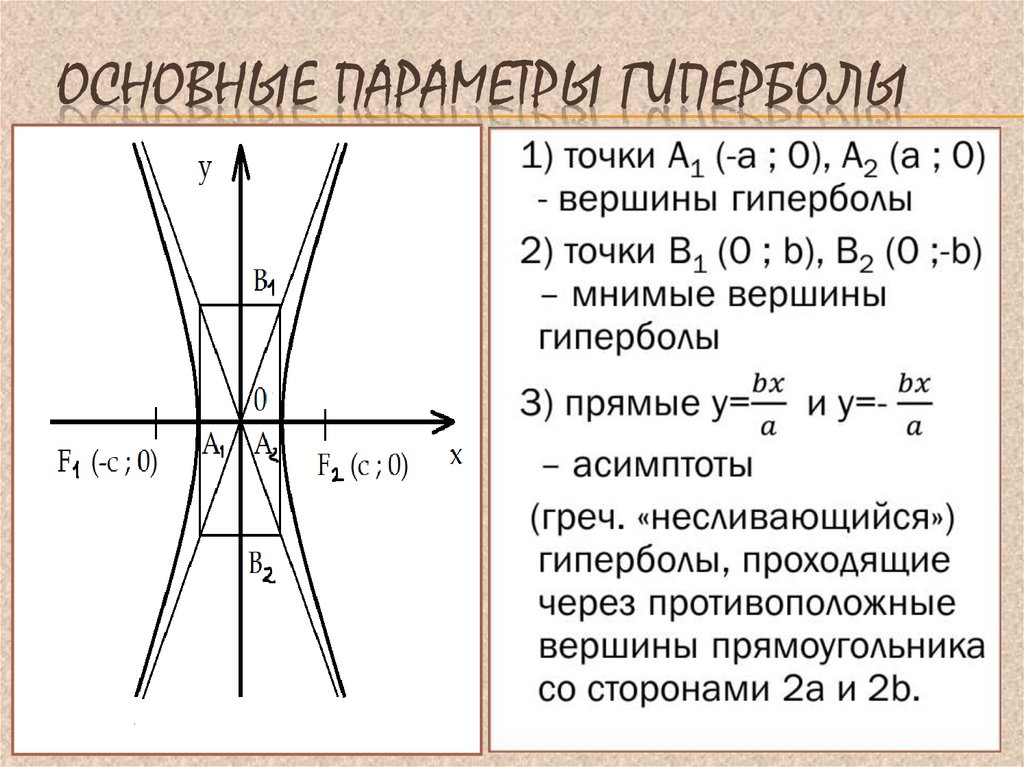
Если гипербола вертикальная, вершины будут расположены по оси Y.

Обязательно учитывайте масштаб и единицы измерения при расчётах.

Воспользуйтесь графическими инструментами для визуализации гиперболы и её вершин.

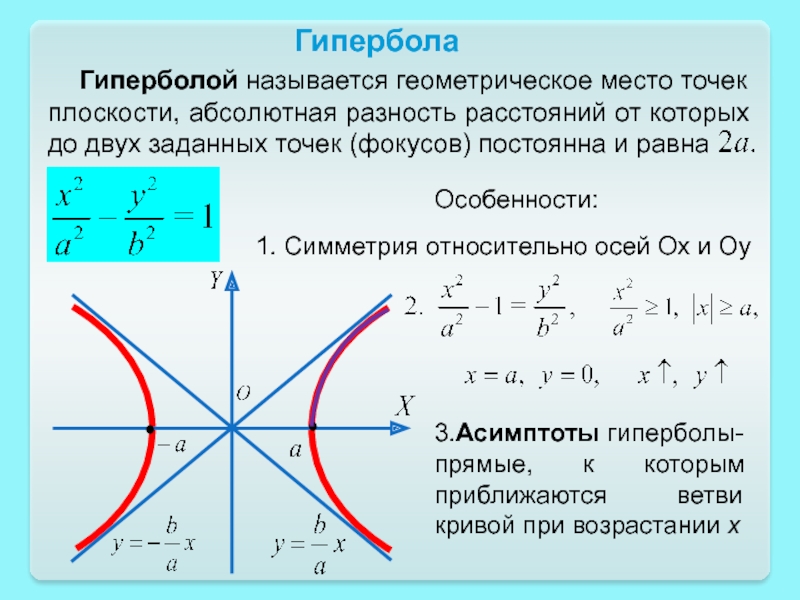
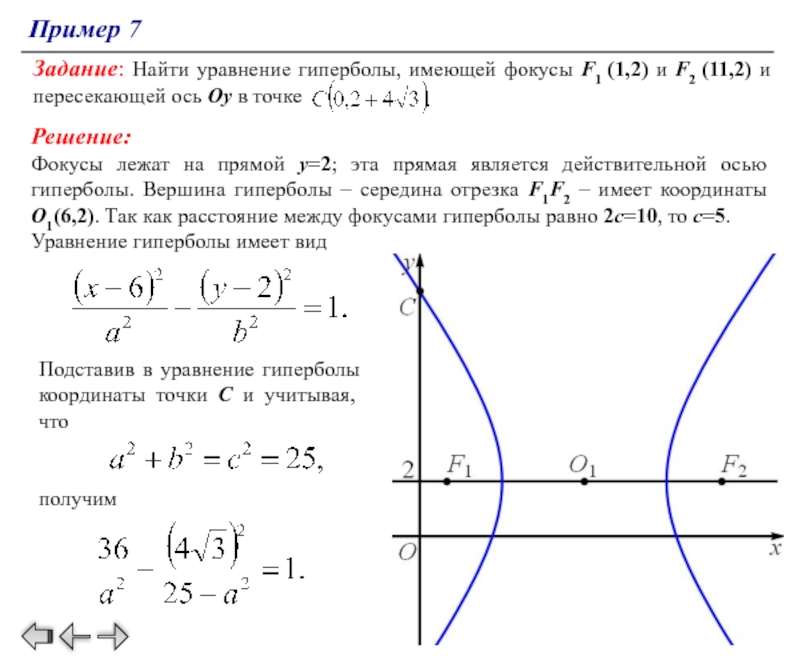
Изучите примеры применения гипербол в физике и инженерии для лучшего понимания.

Регулярно практикуйтесь в решении задач с гиперболами для закрепления материала.