Простые методы для вычисления радиуса окружности, описанной вокруг треугольника

На этой странице вы найдете подборку фотографий и полезных советов о том, как правильно вычислить радиус окружности, описанной около треугольника. Узнайте различные методы и подходы, чтобы легко и быстро справиться с этой задачей.

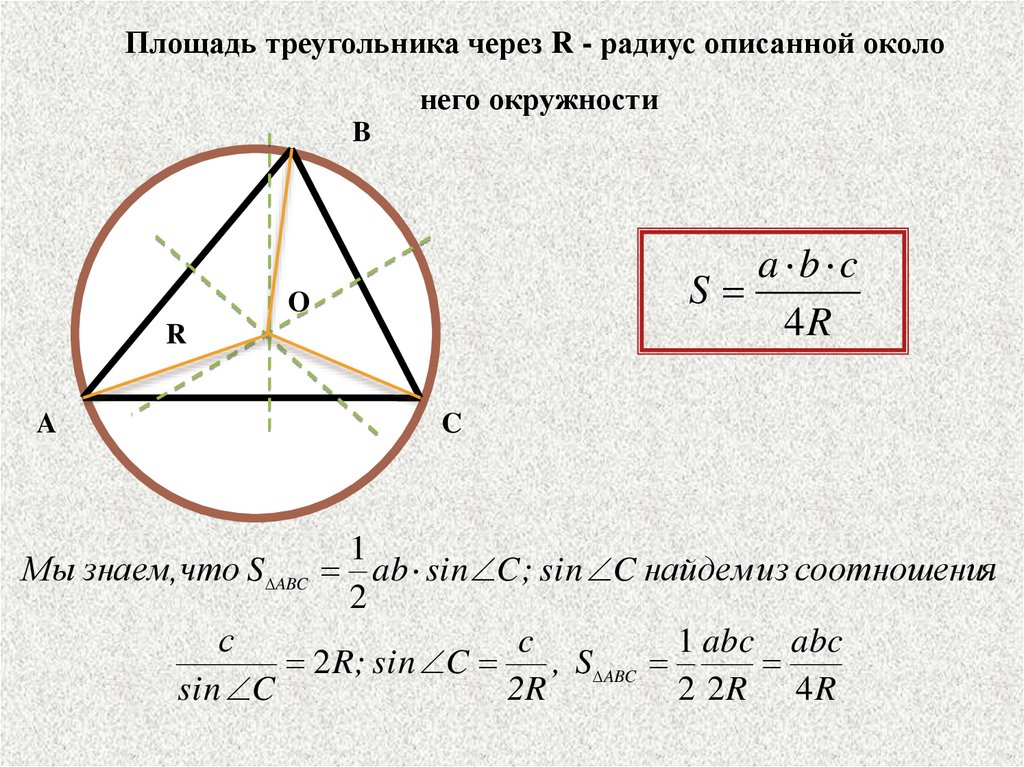
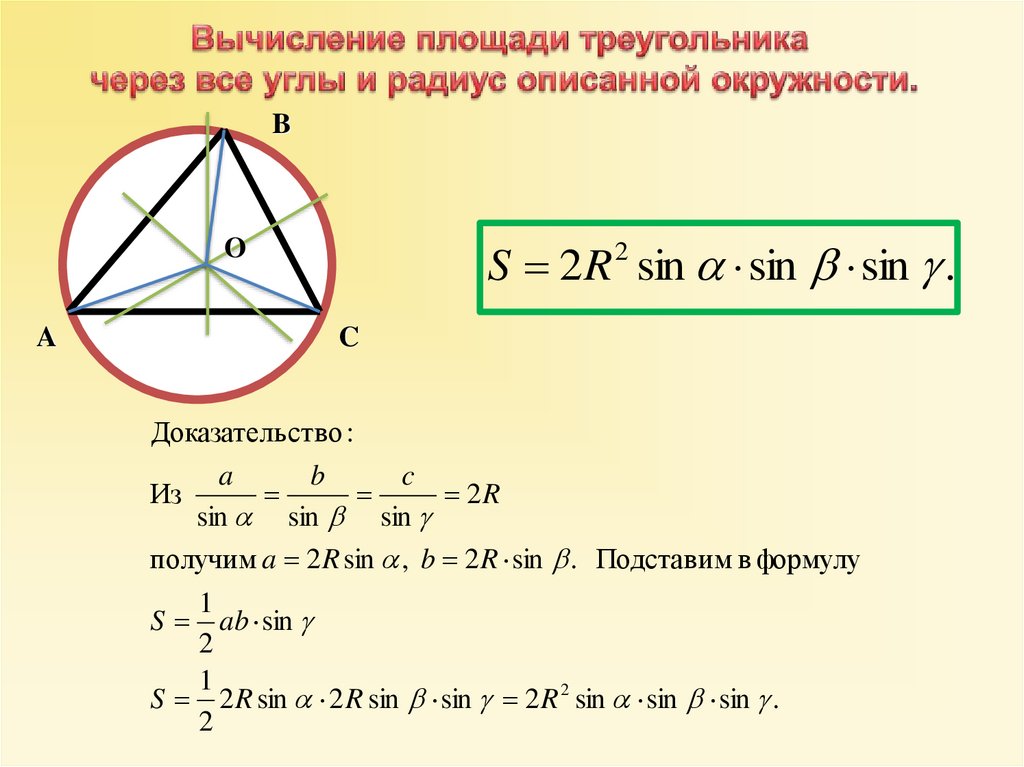
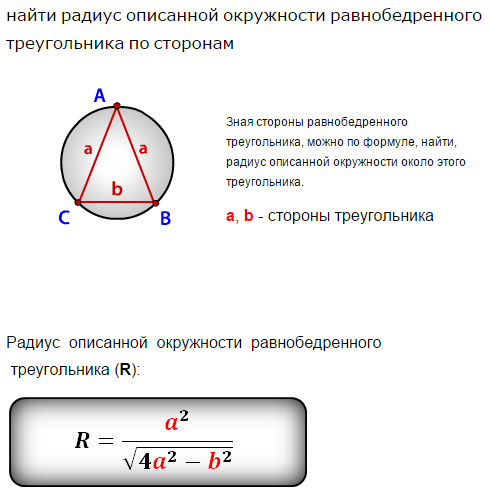
Используйте формулу радиуса описанной окружности через стороны и площадь треугольника: R = (a * b * c) / (4 * S), где a, b и c - стороны треугольника, S - площадь треугольника.

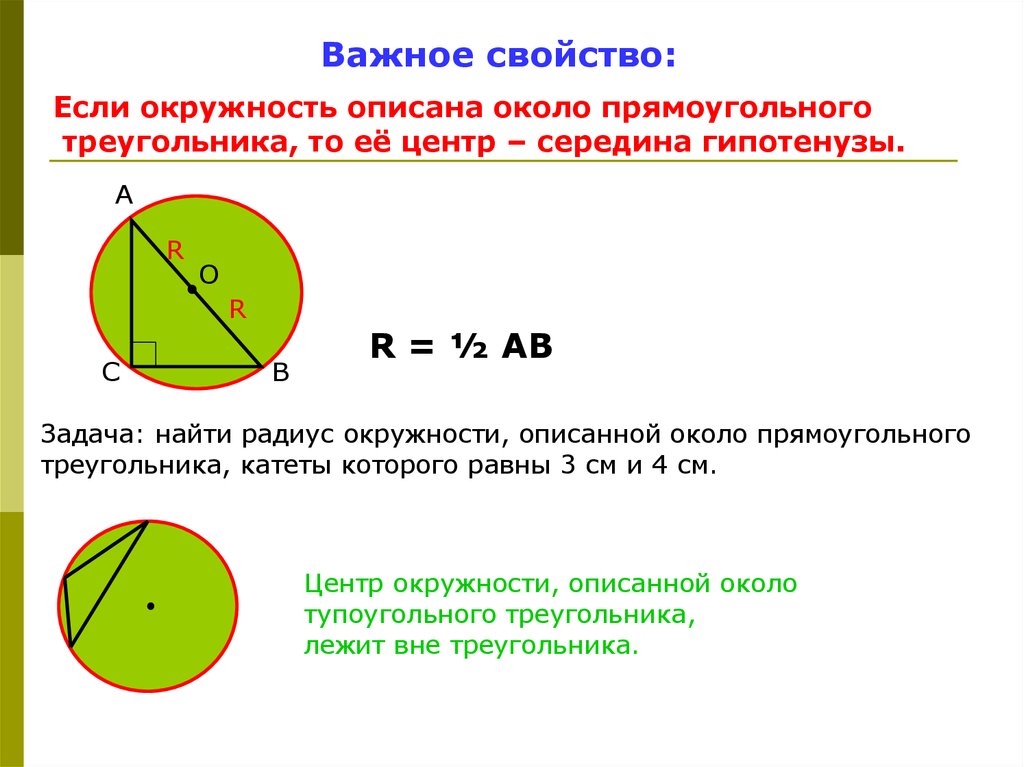
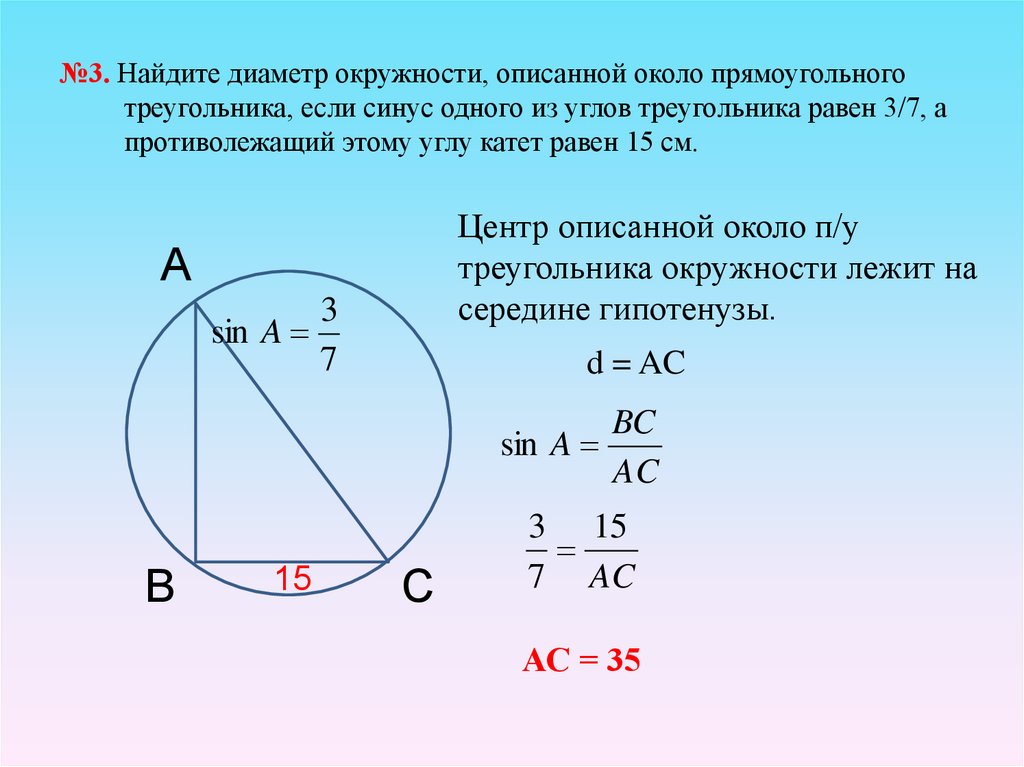
Для прямоугольного треугольника радиус описанной окружности равен половине гипотенузы.

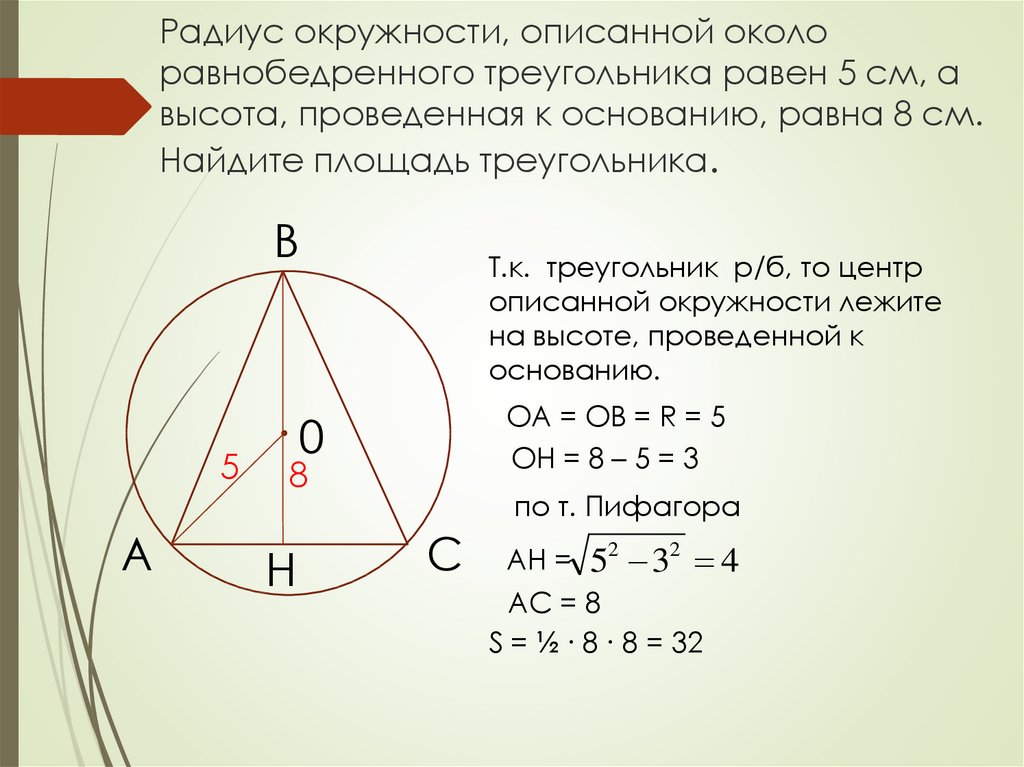
Можно использовать формулу радиуса через угол при вершине и сторону треугольника: R = a / (2 * sin(A)), где A - угол при вершине, a - противолежащая сторона.

Запомните, что радиус описанной окружности всегда больше половины наибольшей стороны треугольника.

Если известны все углы треугольника и одна сторона, используйте формулу: R = a / (2 * sin(A)), где A - угол при вершине, a - противолежащая сторона.

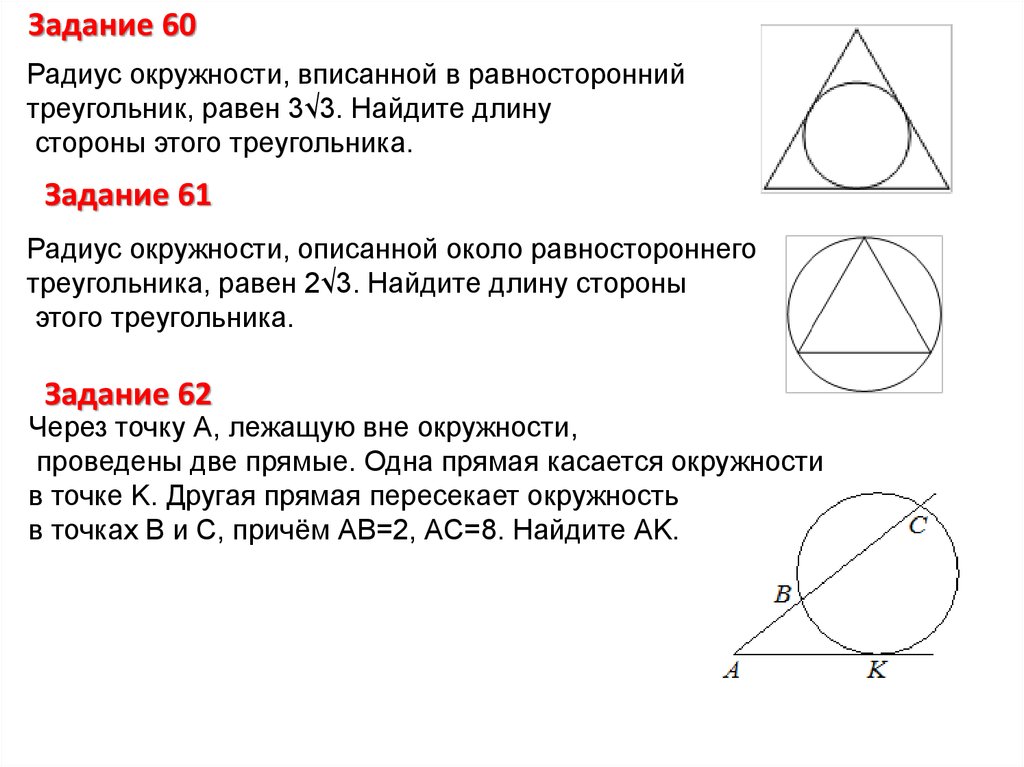
Для равностороннего треугольника радиус описанной окружности вычисляется как: R = a / (sqrt(3)), где a - сторона треугольника.

Помните, что для любого треугольника сумма углов равна 180 градусам, что может помочь в нахождении нужных параметров для вычисления радиуса.

Используйте онлайн-калькуляторы для упрощения процесса вычислений, если вы не уверены в своих расчетах.

Воспользуйтесь графическими редакторами для визуализации треугольника и его описанной окружности для лучшего понимания задачи.

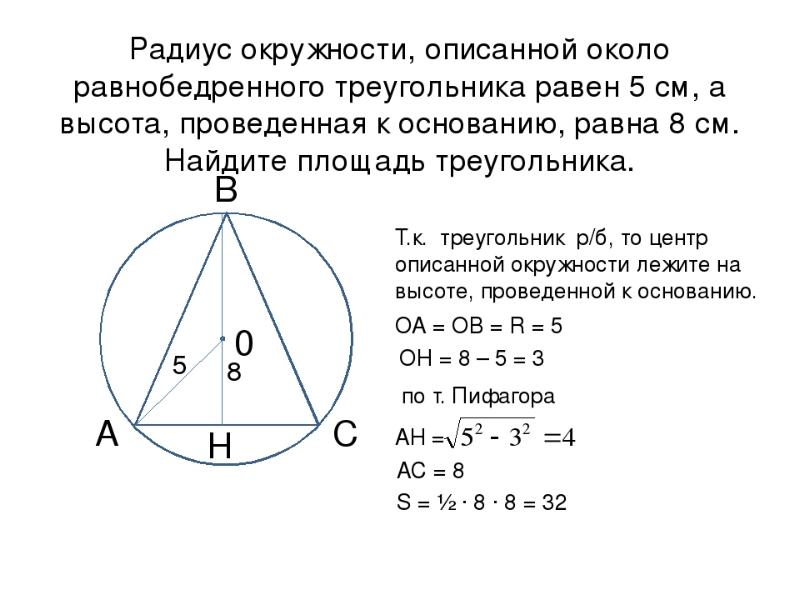
Практикуйтесь на разных типах треугольников, чтобы лучше освоить методы вычисления радиуса описанной окружности.