Методы расчета площади фигуры, заданной уравнениями
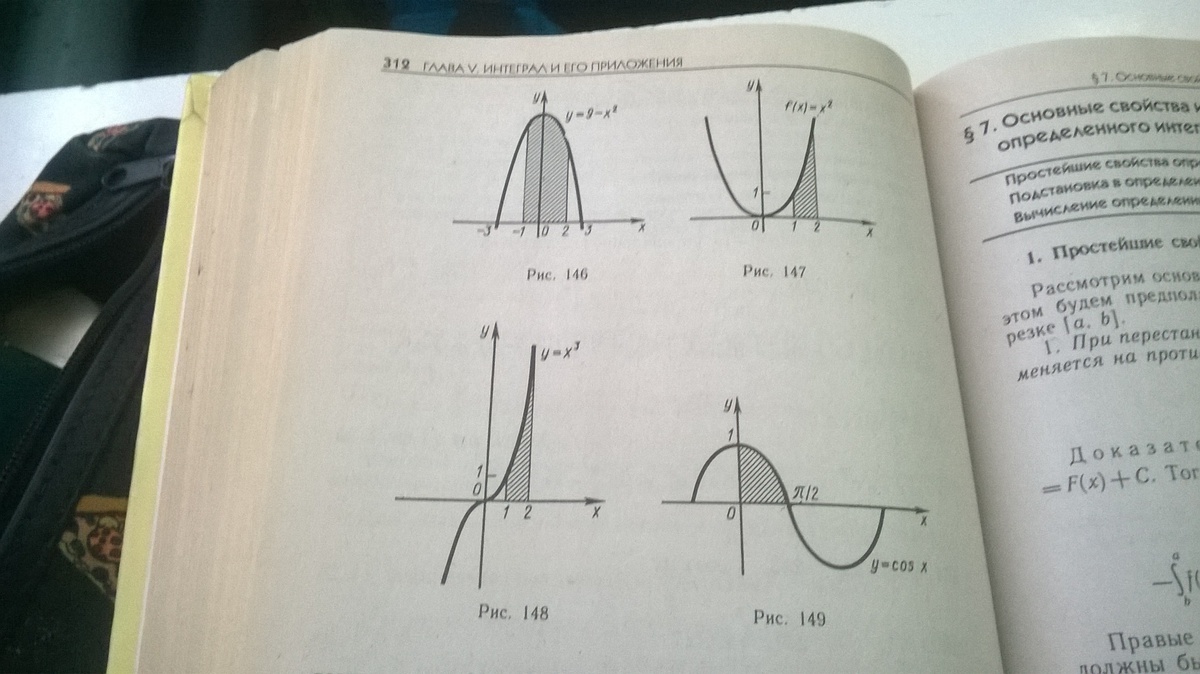
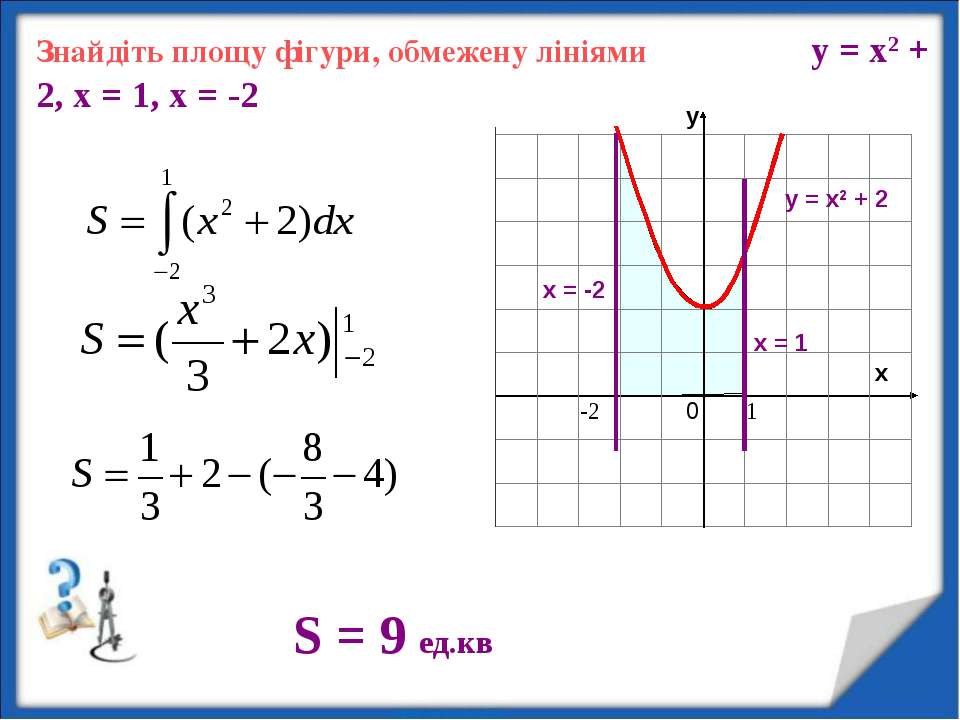
В данном руководстве мы рассмотрим, как вычислить площадь фигуры, ограниченной линиями у = х^3, у = 0 и х = Следуйте нашим советам для успешного выполнения задачи.


Начните с построения графиков всех уравнений, чтобы визуально понять область, ограниченную линиями.
Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.

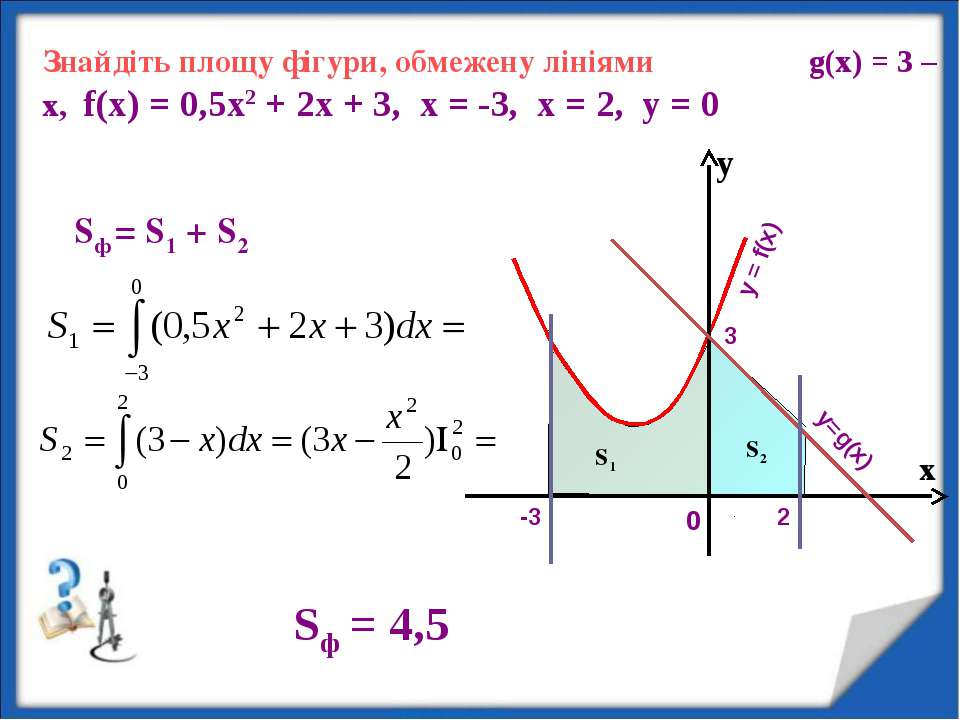
Обратите внимание на точки пересечения графиков, так как они определяют границы интегрирования.
Найти площадь фигуры, ограниченной линиями. Пример 3.
Используйте определенный интеграл для нахождения площади под кривой у = х^3 от х = 0 до х = 2.
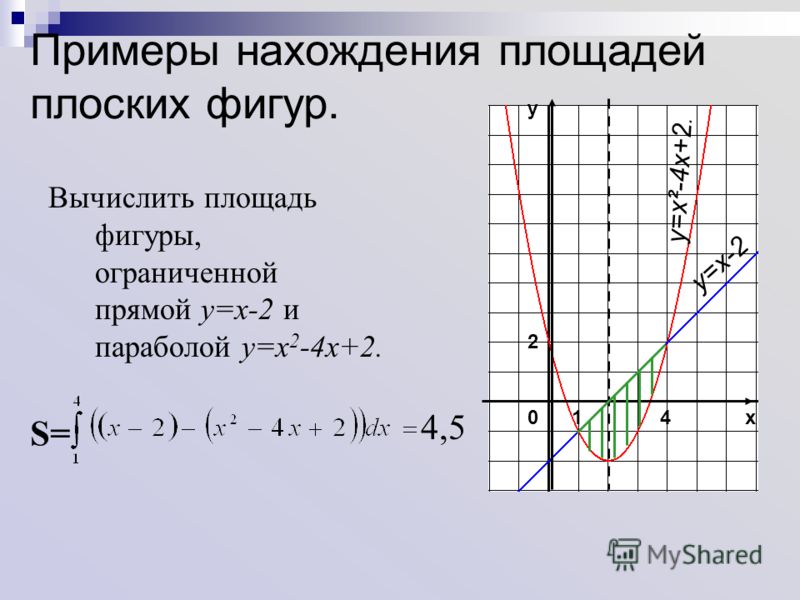

Помните, что интеграл функции f(x) от a до b равен ∫[a,b] f(x) dx.

Для функции y = x^3 интеграл будет ∫[0,2] x^3 dx.
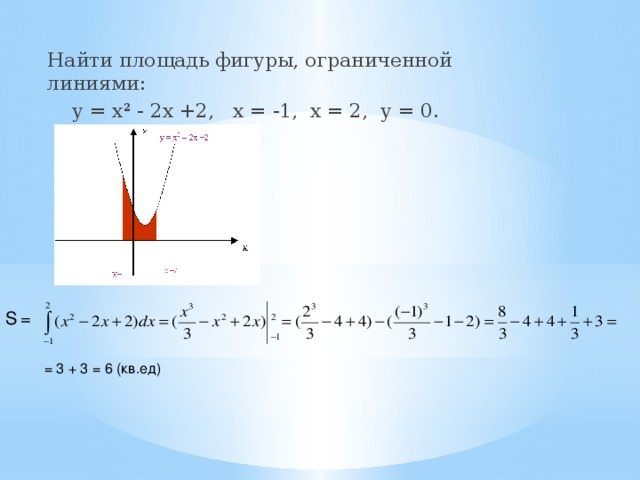

Рассчитайте интеграл, используя стандартные методы интегрирования: ∫ x^3 dx = (x^4/4).
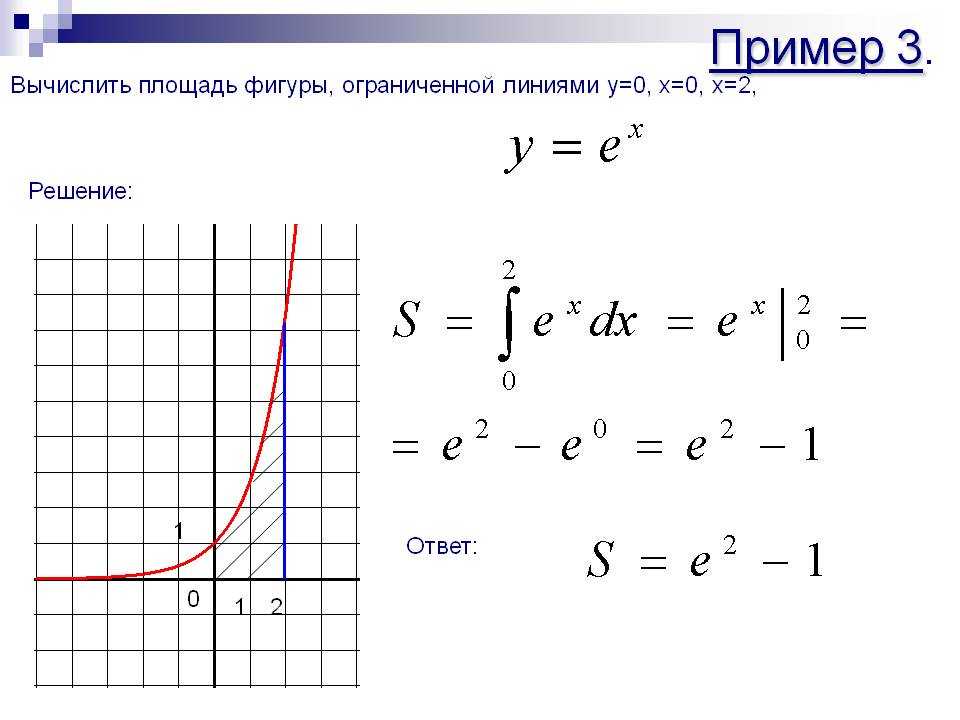
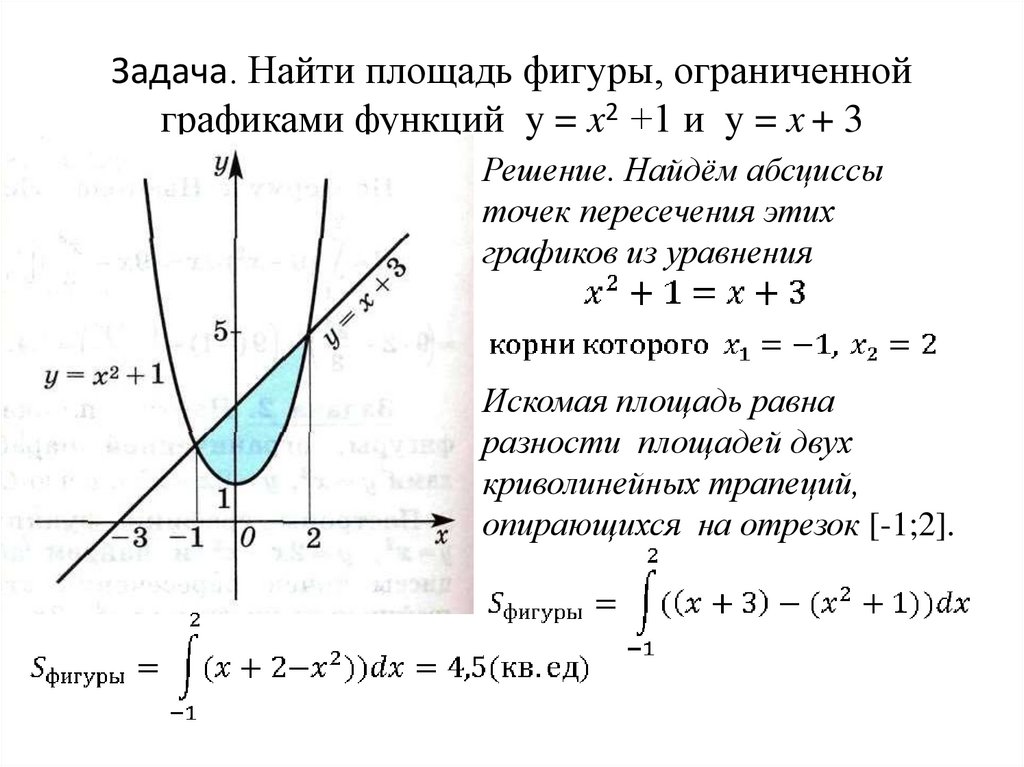
Вычислите значение интеграла на границах: [(2^4)/4] - [(0^4)/4].

Проверьте правильность расчетов: площадь равна (16/4) - 0 = 4 квадратных единиц.
Используйте графические калькуляторы или программное обеспечение для проверки результата.
Если возникают сложности, обратитесь за помощью к учителю или воспользуйтесь учебными ресурсами онлайн.