Практическое руководство по биссектрисам в треугольниках

Биссектриса треугольника — это отрезок, который делит угол треугольника на две равные части. В этой статье вы найдете полезные советы и фотографии, которые помогут вам лучше понять и использовать это важное геометрическое понятие.

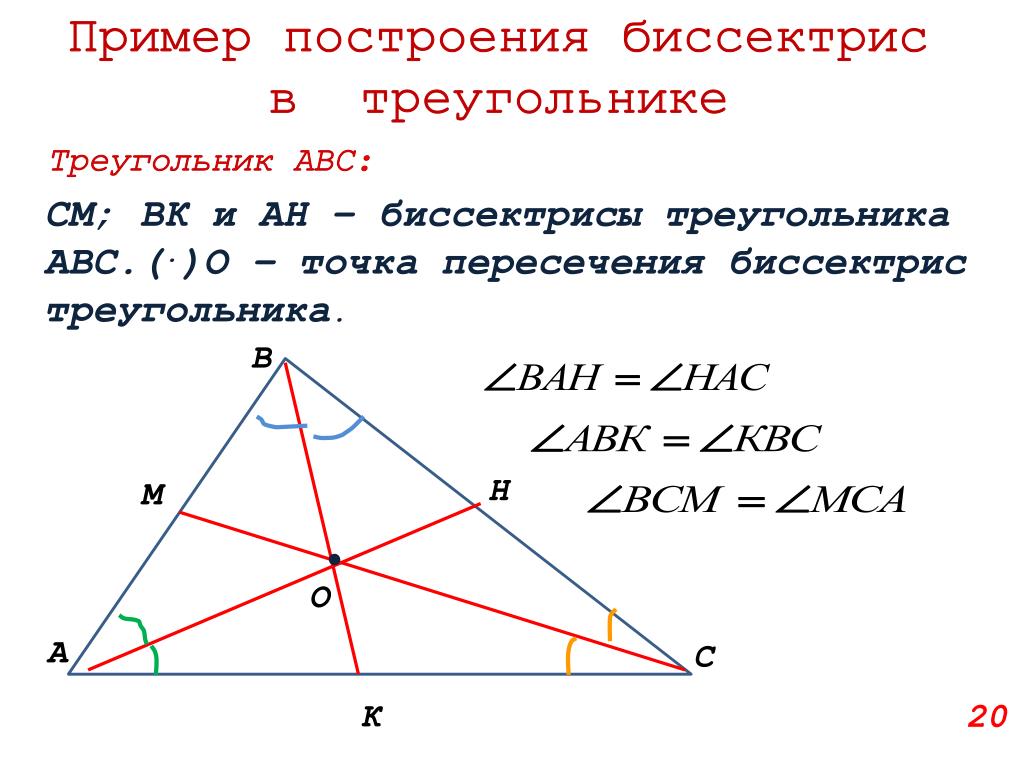
Изучите теорему о биссектрисе, чтобы понимать, как она делит противоположную сторону на два отрезка, пропорциональные соседним сторонам угла.

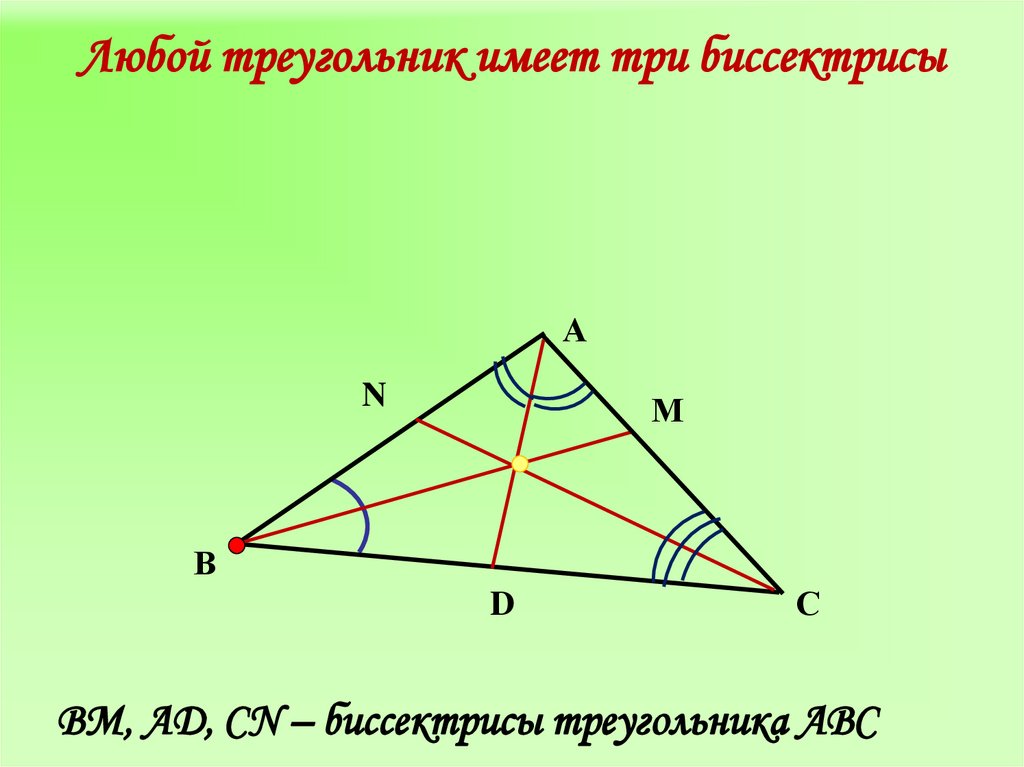
Помните, что каждая вершина треугольника имеет свою биссектрису, и все три биссектрисы пересекаются в одной точке — инцентре треугольника.

Используйте циркуль и линейку для построения биссектрисы. Это поможет вам понять точные шаги этого процесса.

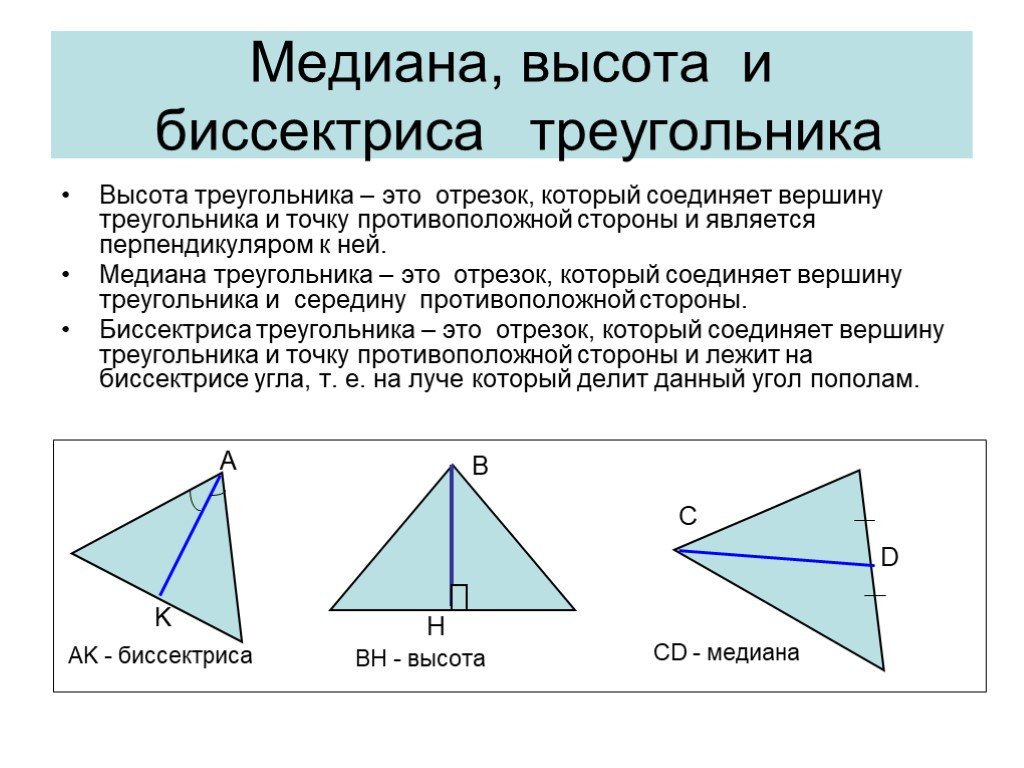
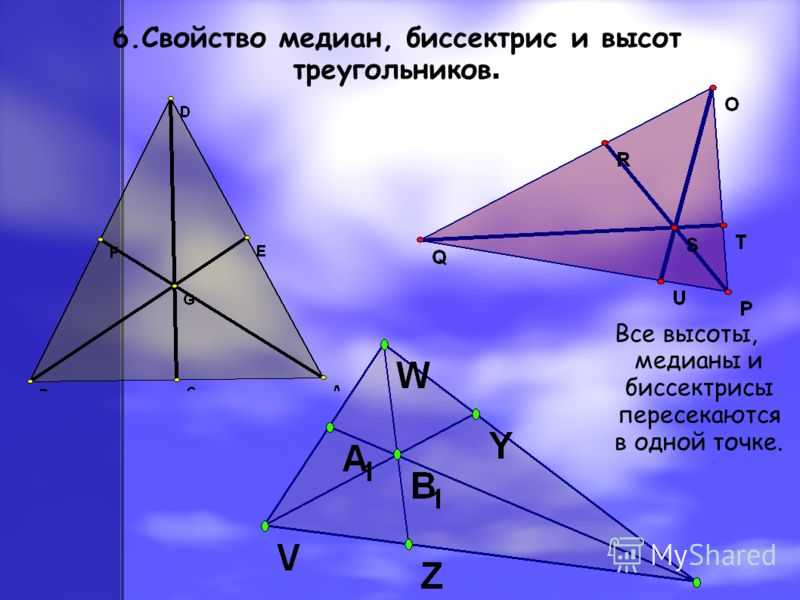
Изучите свойства инцентра, который является точкой пересечения всех биссектрис треугольника и центром вписанной окружности.

Практикуйте построение биссектрис на различных типах треугольников: остроугольных, тупоугольных и прямоугольных.

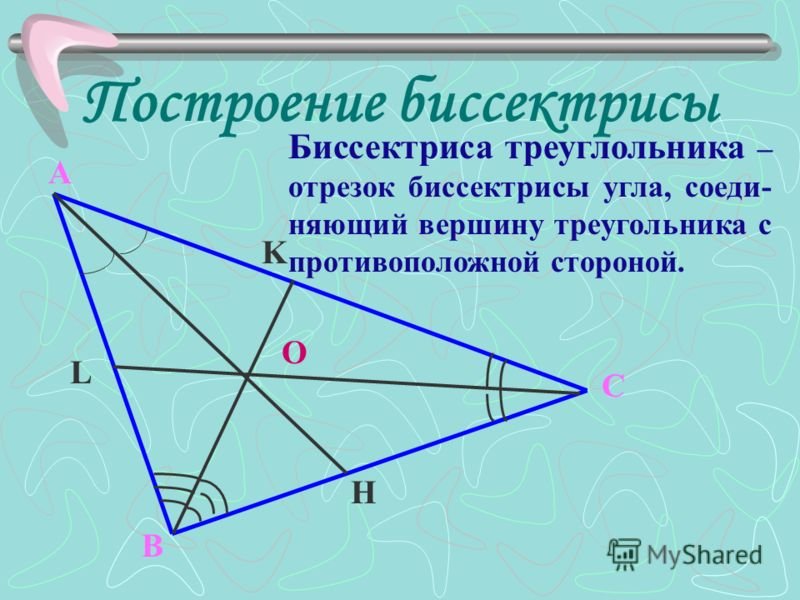
Обратите внимание на отношения сторон и углов в треугольнике, чтобы лучше понимать, как биссектрисы влияют на их пропорции.

Используйте программное обеспечение для геометрии, такое как GeoGebra, чтобы проверить свои построения и эксперименты с биссектрисами.

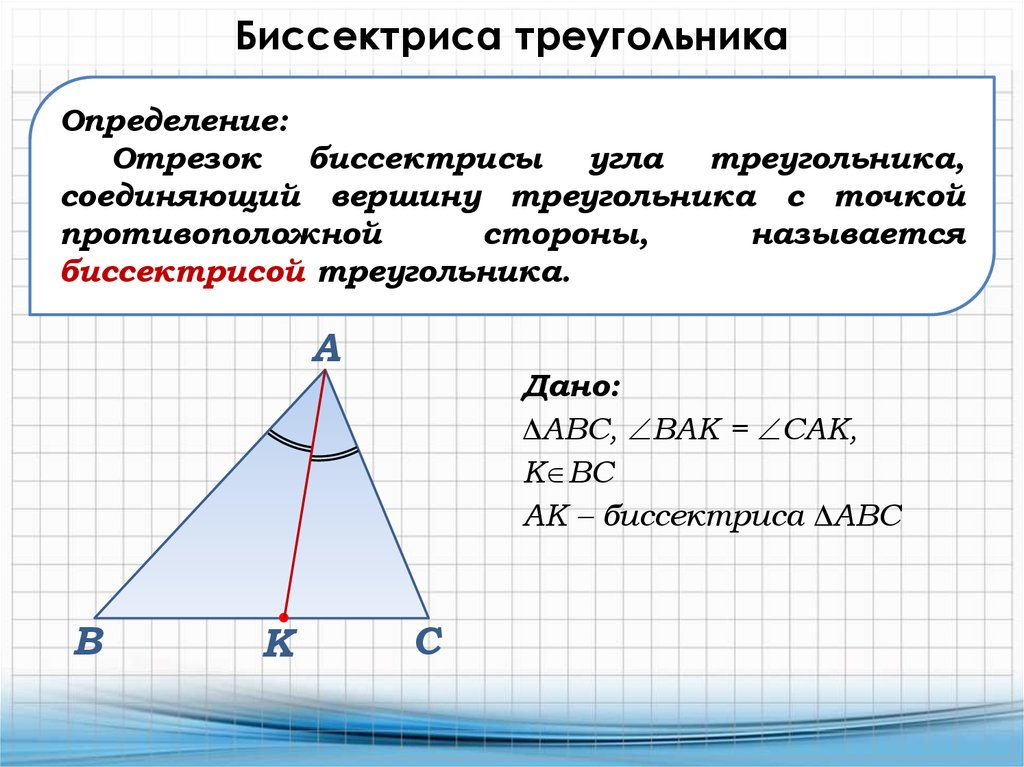
Изучите реальные приложения биссектрис, например, в архитектуре и инженерии, чтобы увидеть их практическую ценность.

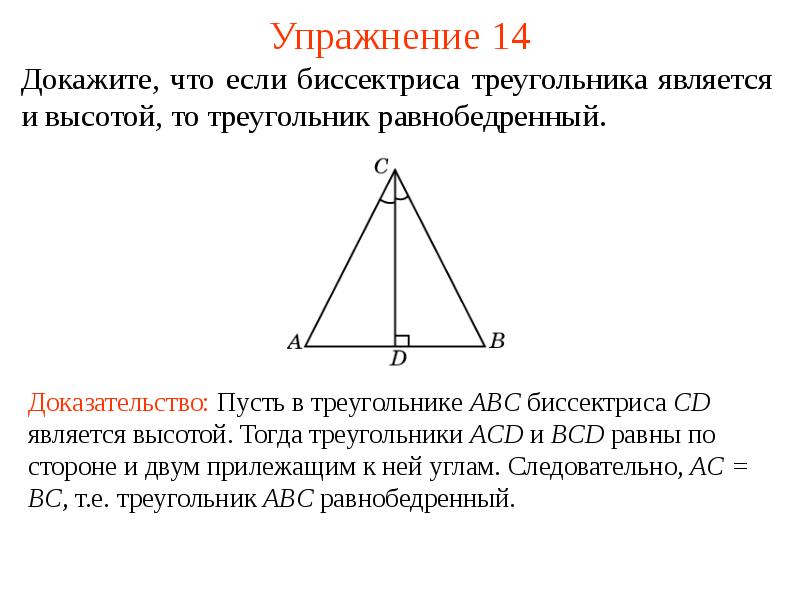
Часто проверяйте свои знания с помощью задач и упражнений, чтобы закрепить понимание теоретических аспектов.

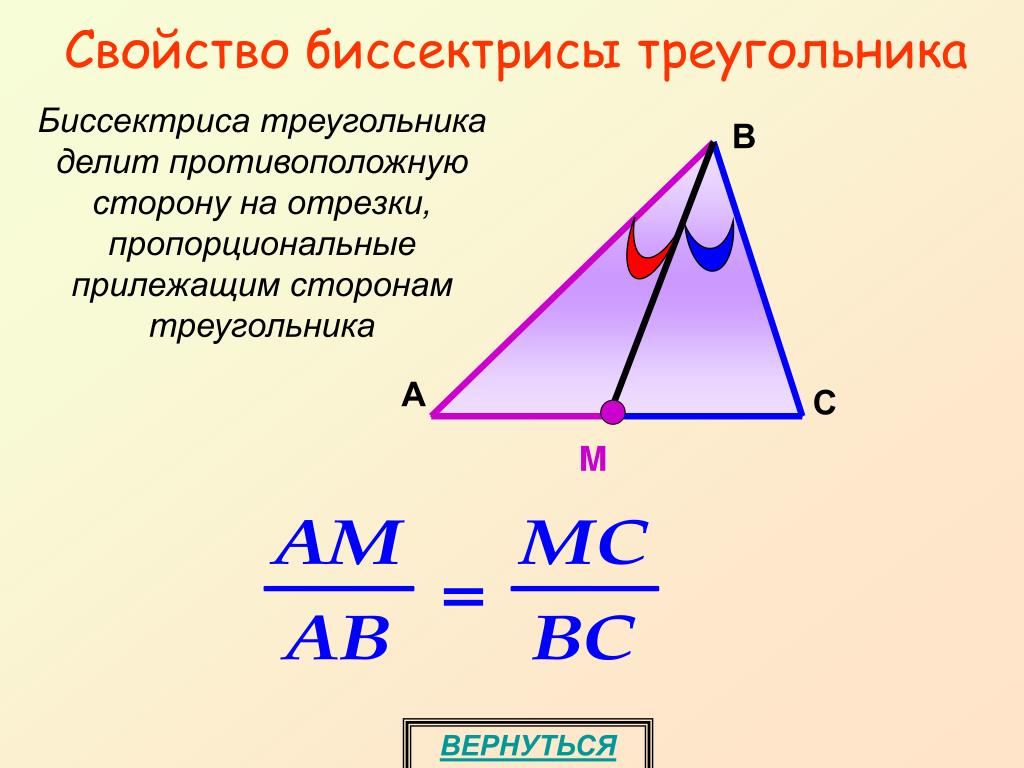
Не забывайте изучать теоремы и доказательства, связанные с биссектрисами, чтобы глубже понять их математическую природу.