Соотношения при делении биссектрисами треугольника
Биссектрисы треугольника - это отрезки, которые делят углы треугольника пополам и пересекаются в одной точке, называемой инцентром. Эти свойства помогают решать множество задач по геометрии.
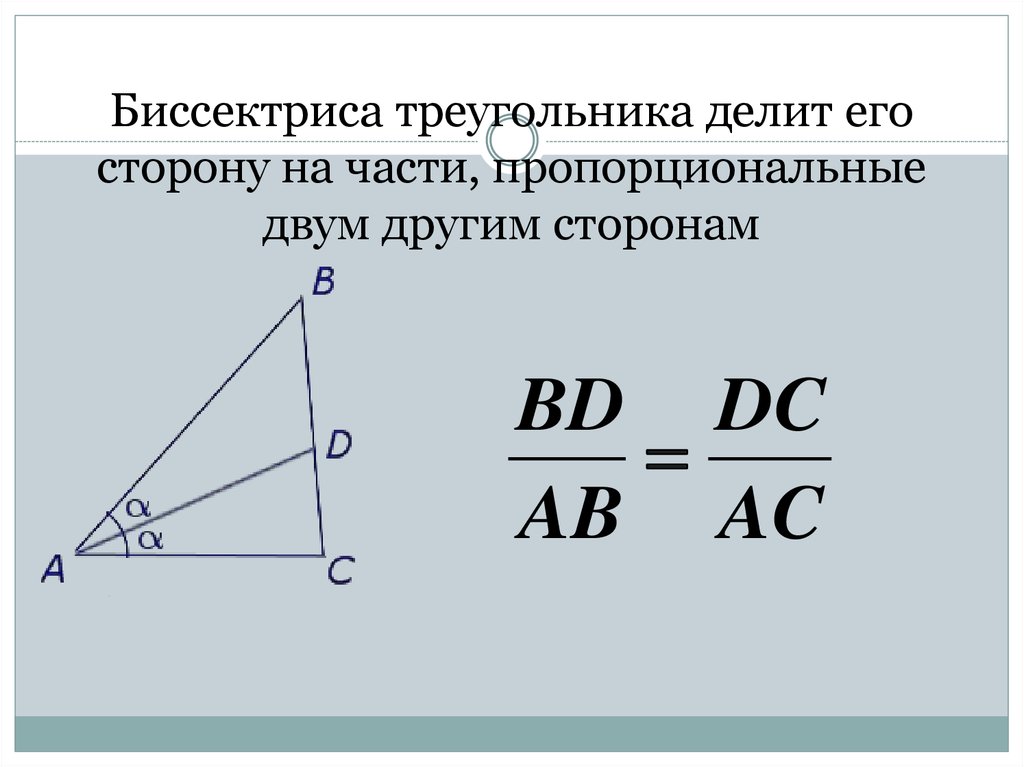
Запомните, что биссектрисы делят противоположную сторону в отношении длин смежных сторон.

Для нахождения длины биссектрисы используйте формулу биссектрисы в треугольнике.
Задание 26 Отношение площадей Свойство биссектрисы
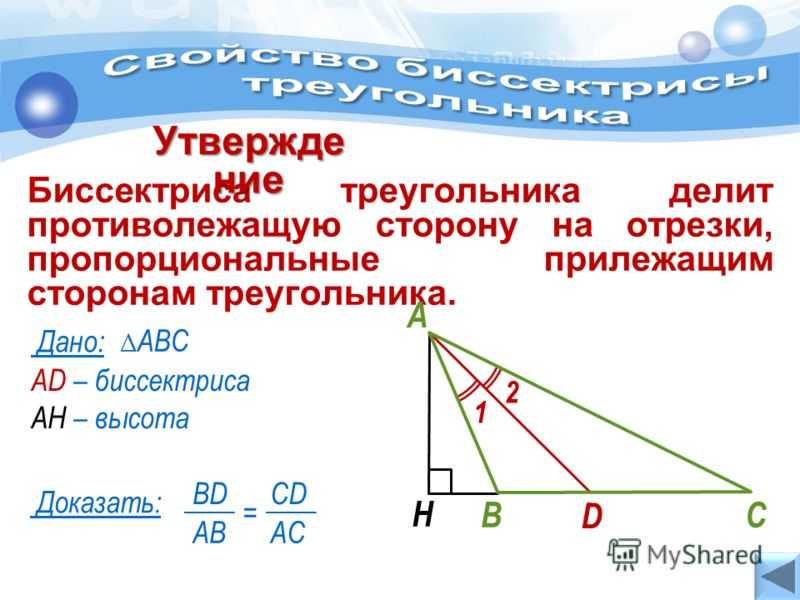

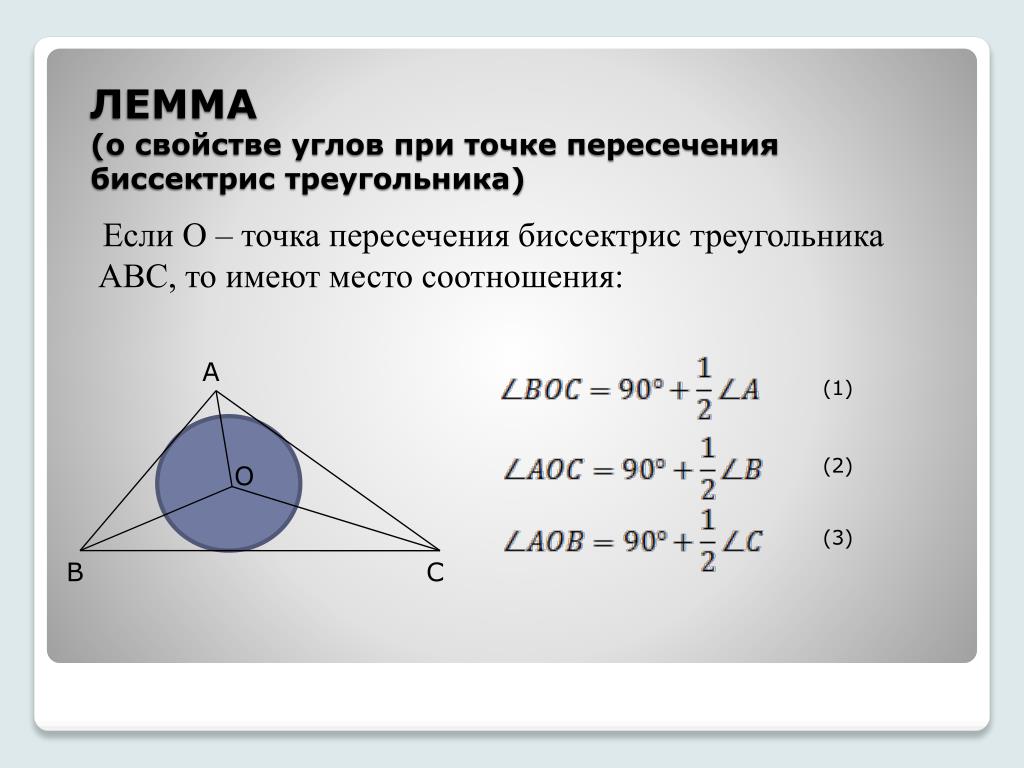
Точка пересечения всех трех биссектрис треугольника называется инцентр, и она является центром вписанной окружности.
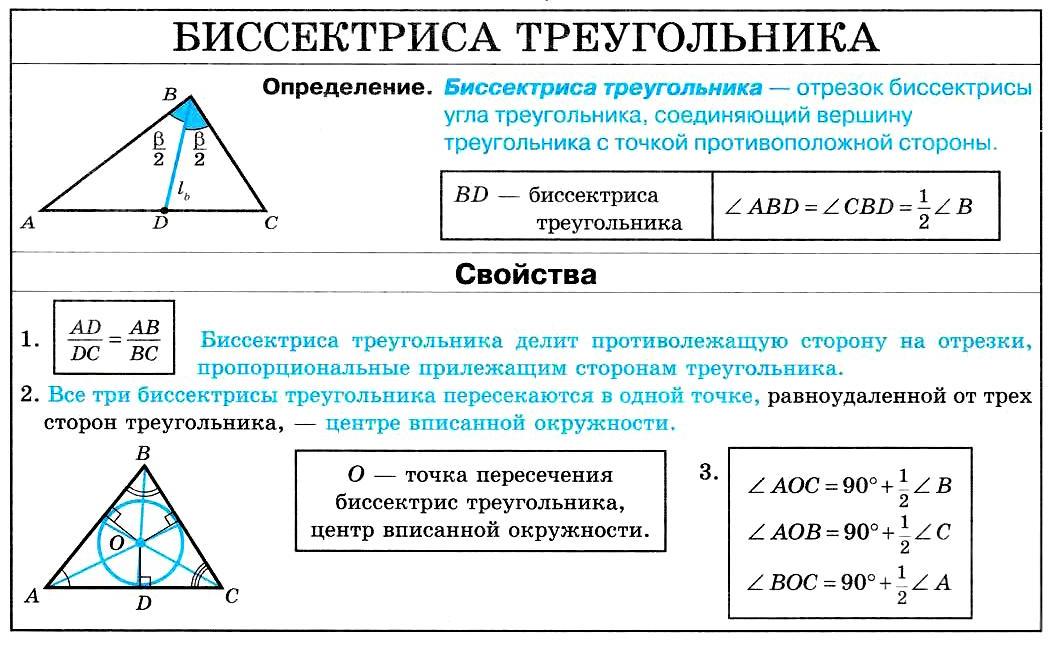
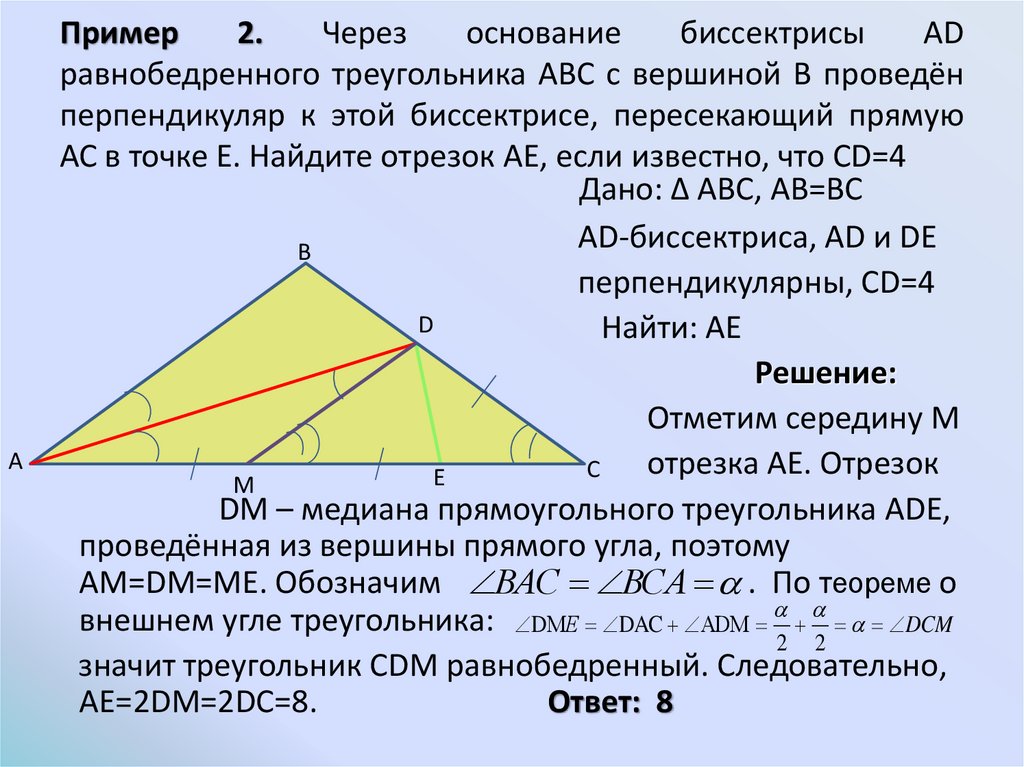
Используйте теорему о биссектрисе для доказательства равенства углов в сложных задачах.
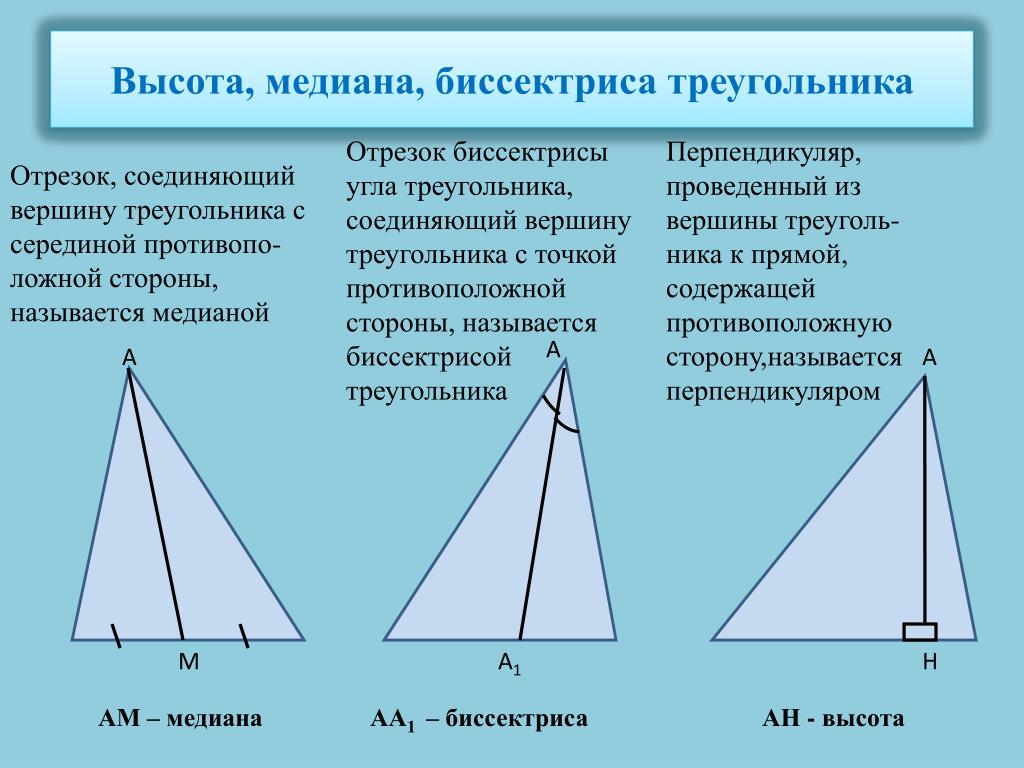
Треугольник. Часть 2. Медиана, биссектриса, высота.
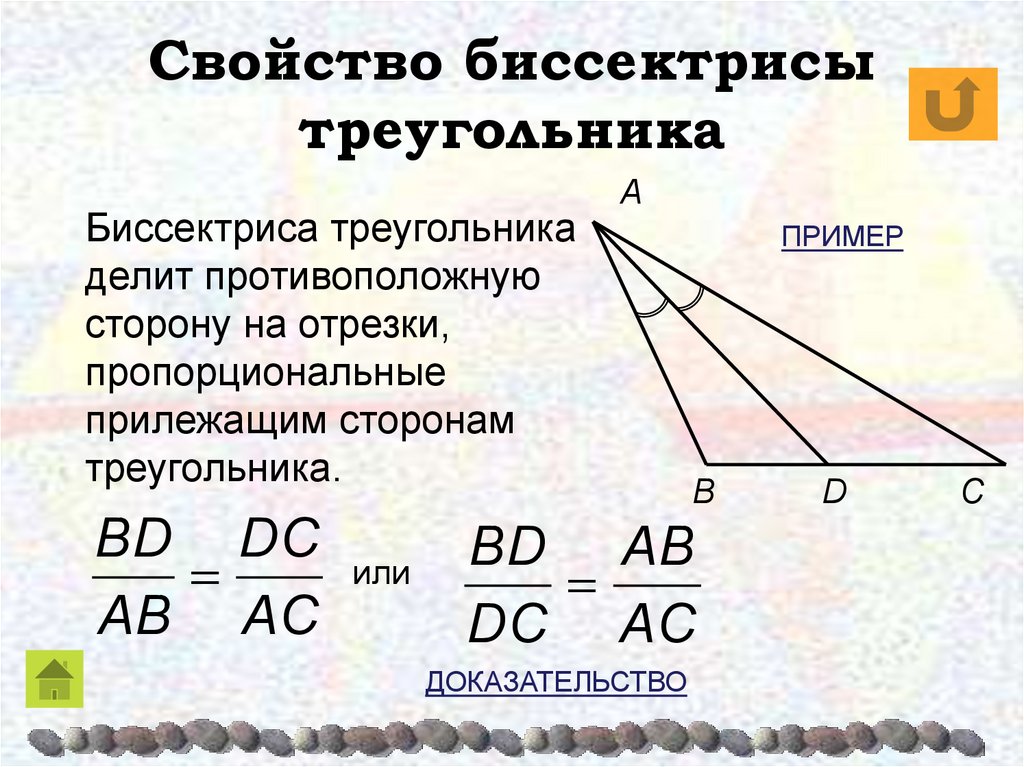
При решении задач на биссектрисы полезно использовать свойства пропорциональности.

В равнобедренном треугольнике биссектрисы совпадают с медианами и высотами.
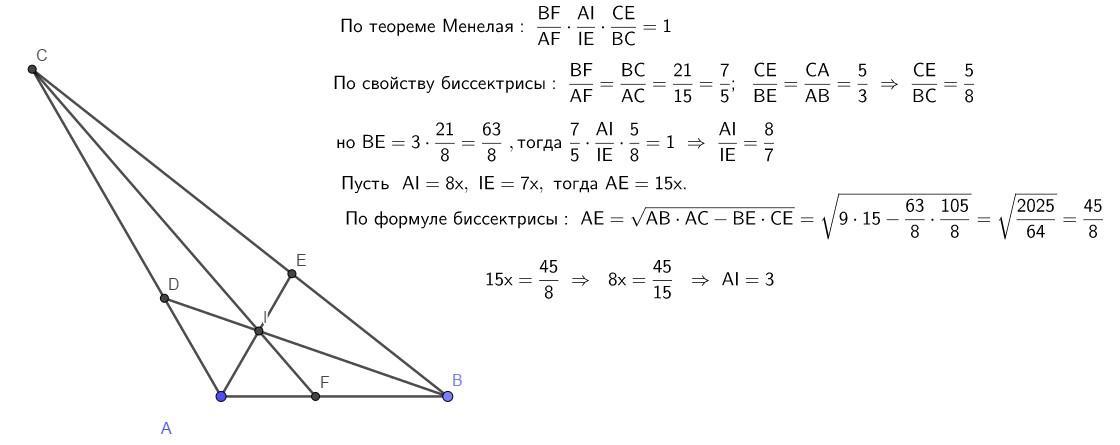
Проверьте, правильно ли вы построили биссектрису, используя циркуль и линейку.

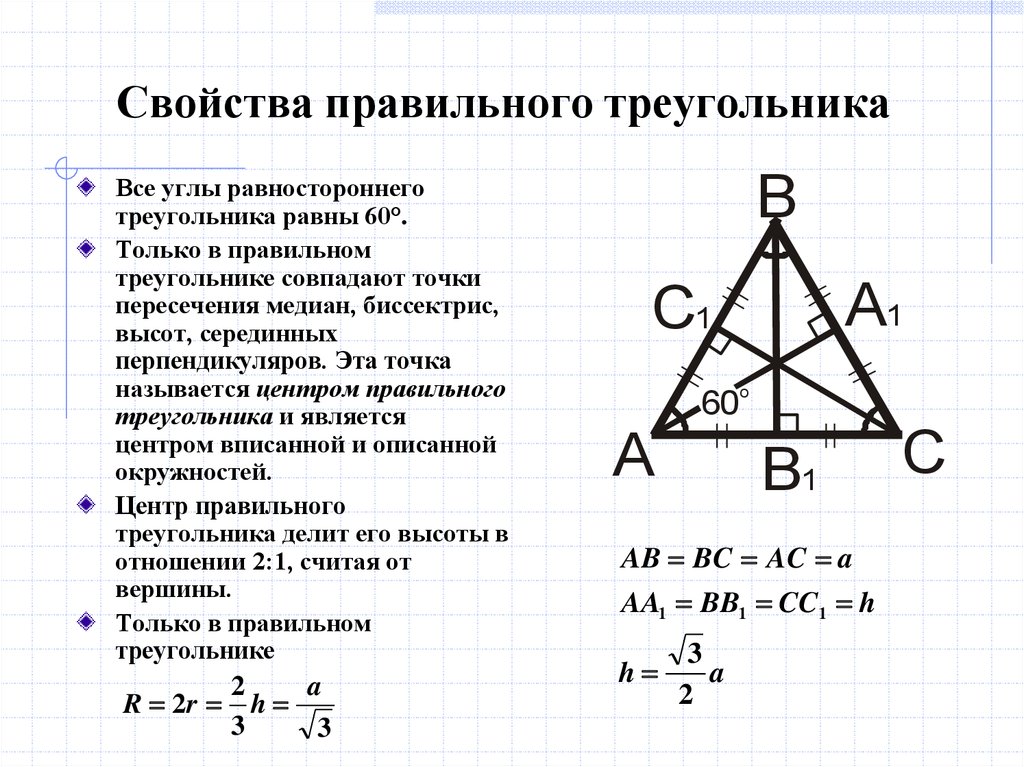
На практике биссектрисы помогают в строительстве и дизайне, где важно точное деление углов.
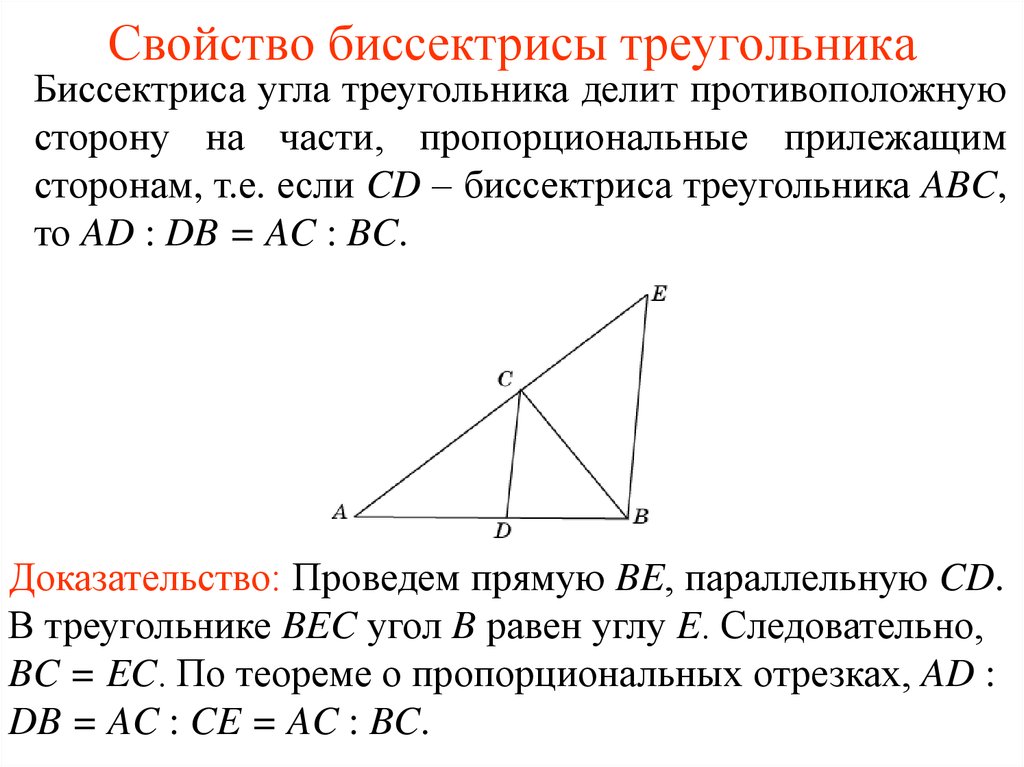
Свойство биссектрисы треугольника с доказательством
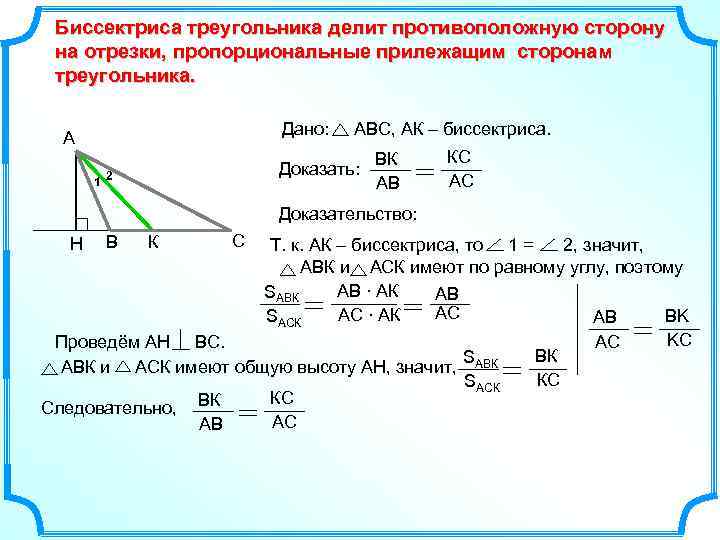
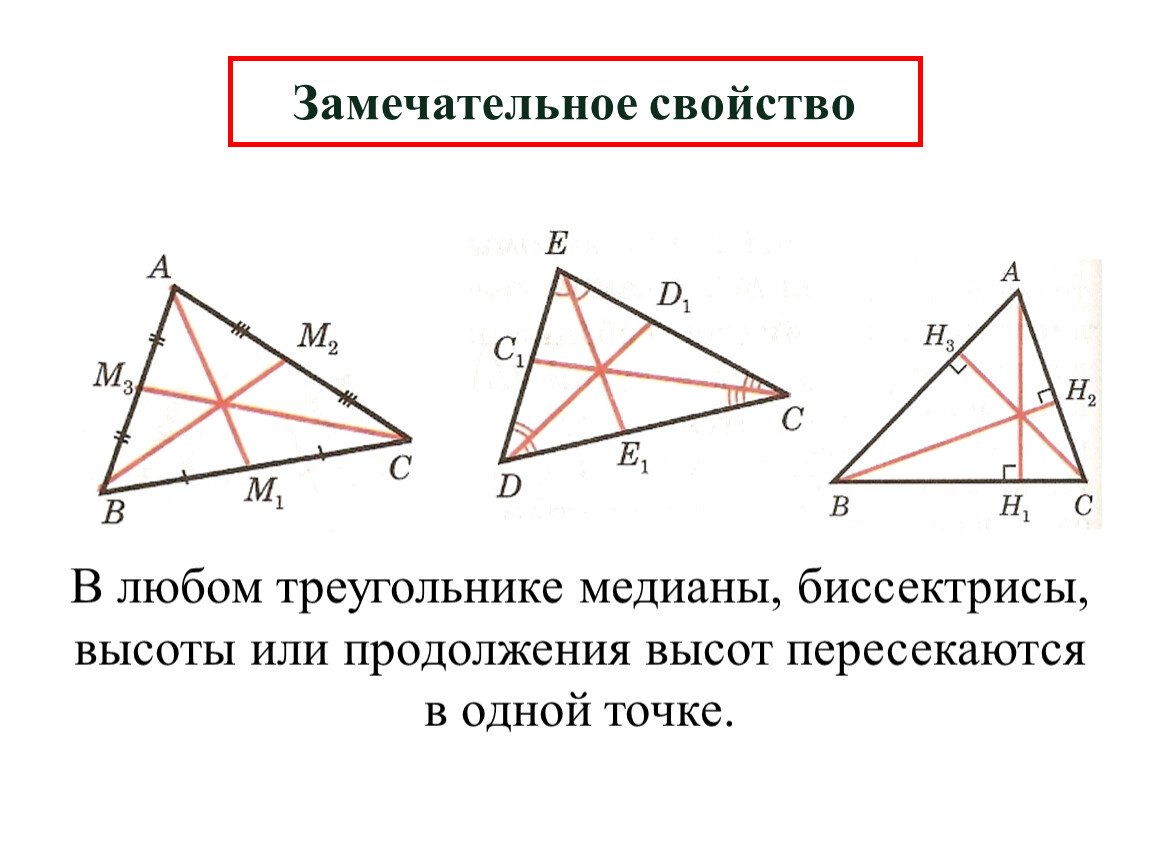
Изучите примеры задач с использованием биссектрис для лучшего понимания их свойств.
Геометрия Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1
Вспомните, что сумма длин отрезков, на которые биссектрисы делят стороны треугольника, равна периметру треугольника.