Основные принципы построения эллипса: формулы и примеры
Эллипс является одной из ключевых кривых второго порядка в геометрии. На этой странице вы найдете подборку фотографий, иллюстрирующих различные способы построения эллипсов, а также полезные советы по использованию соответствующих формул.



Всегда начинайте построение эллипса с определения его основных осей: большой и малой осей.
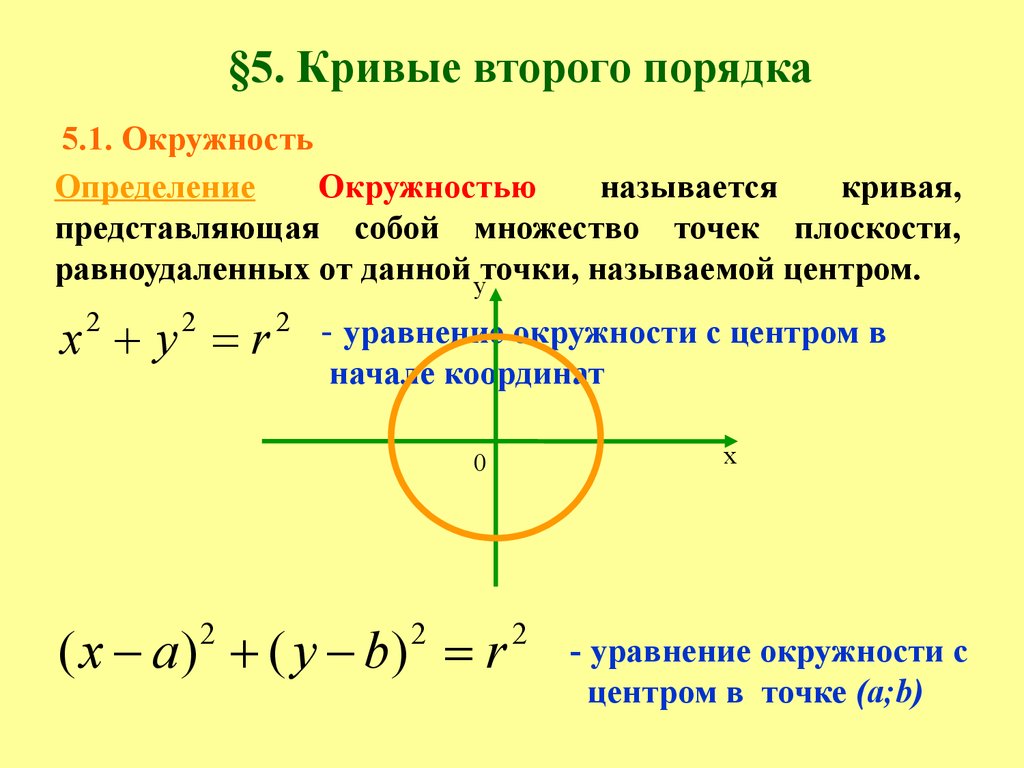
Лекция 31.1. Кривые второго порядка. Эллипс

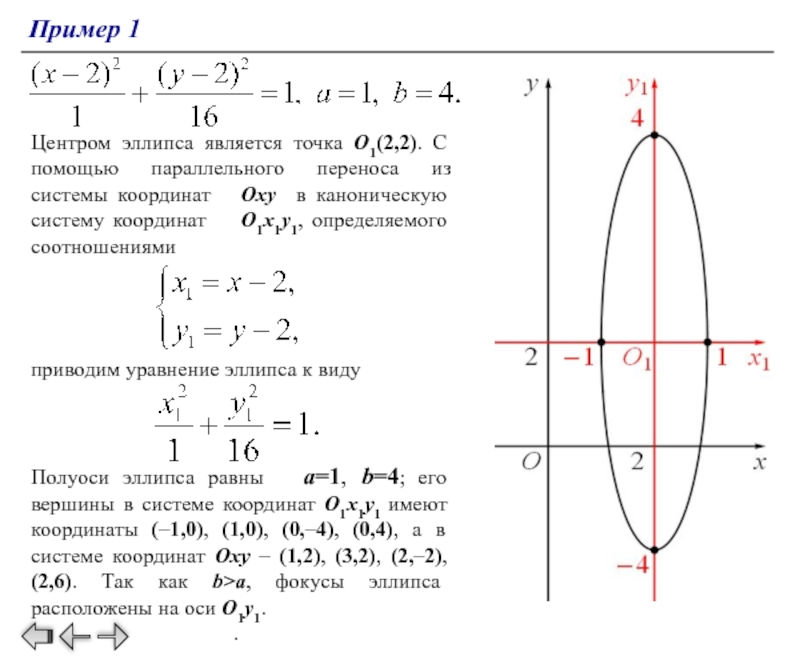
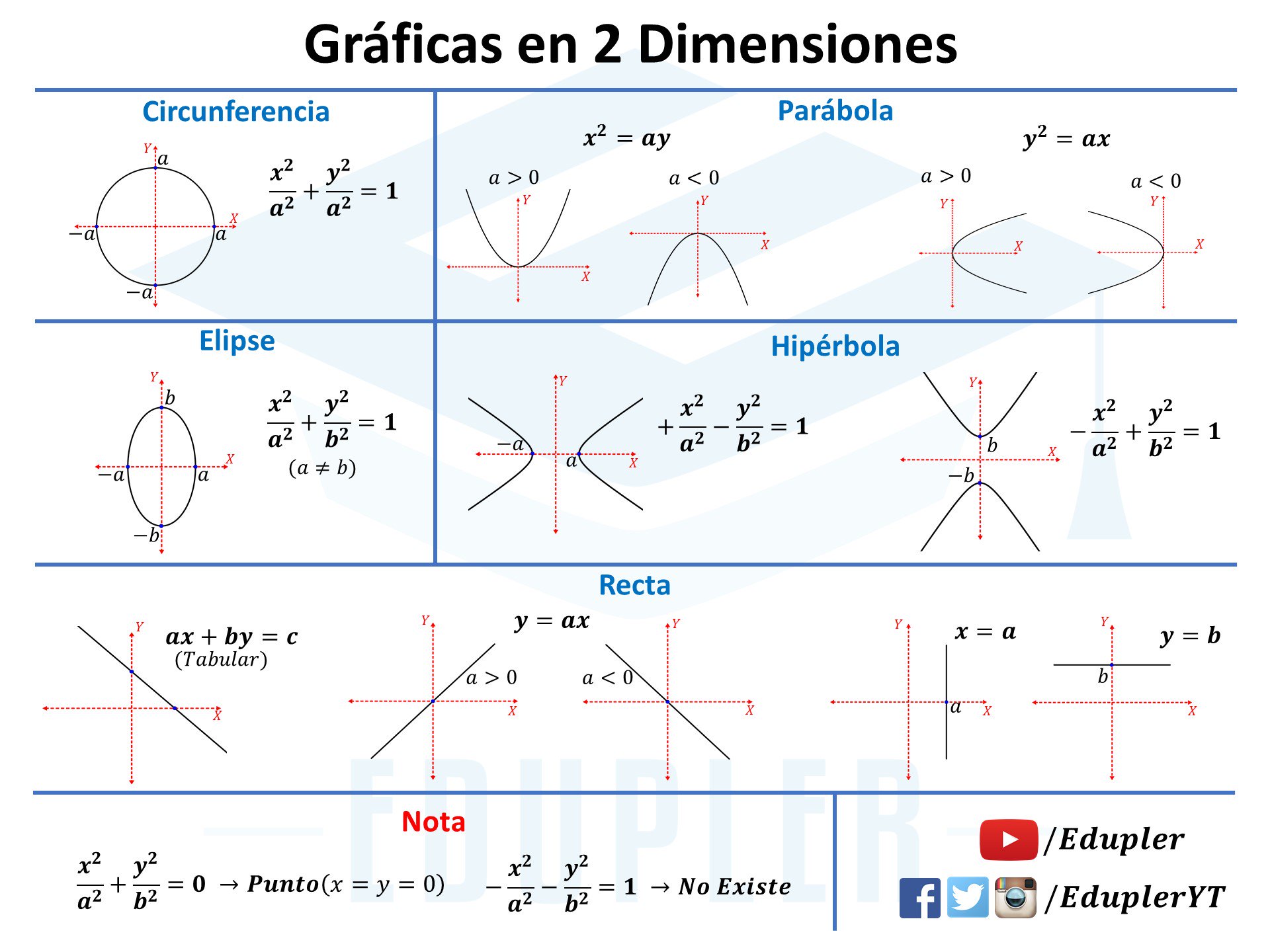
Используйте уравнение эллипса в стандартной форме: (x^2 / a^2) + (y^2 / b^2) = 1, где a и b - длины полуосей.
Математика без Ху%!ни. Кривые второго порядка. Эллипс.

Для точного построения эллипса применяйте метод фокальных точек: сумма расстояний от любой точки эллипса до двух фокусов равна длине большой оси.
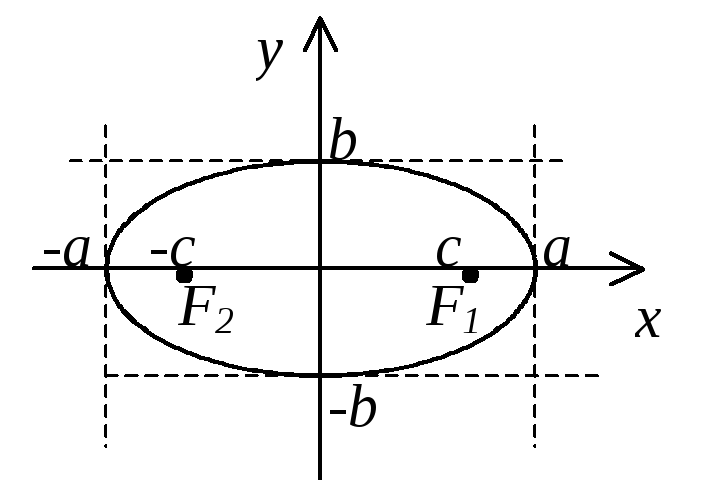

Применяйте геометрические инструменты, такие как циркуль и линейка, для точного черчения эллипса.

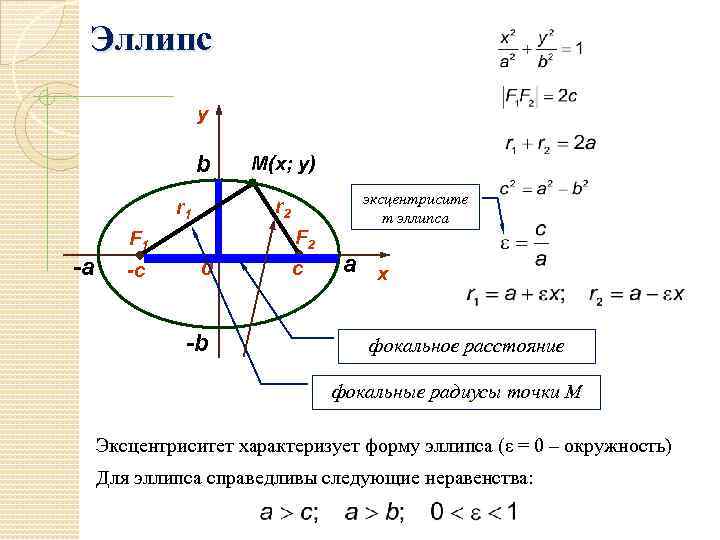
Для вычисления площади эллипса используйте формулу: S = πab, где a и b - полуоси эллипса.
Кривые второго порядка

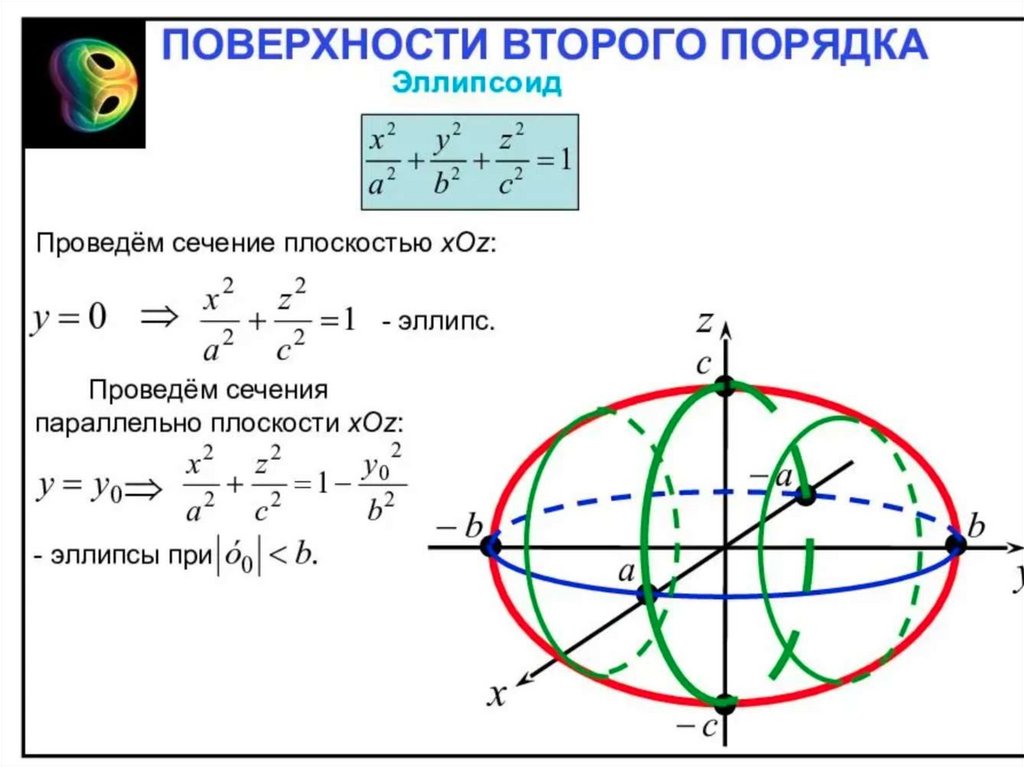
Обратите внимание на симметрию эллипса относительно его главных осей при построении и проверке.

При работе с уравнениями эллипса в полярных координатах используйте соответствующую форму: r = (ab) / √(b^2 cos^2(θ) + a^2 sin^2(θ)).
Проверьте свои построения, используя программное обеспечение для черчения, чтобы избежать ошибок.

Для более сложных задач используйте численные методы и программирование для точного моделирования эллипсов.
Определить тип кривой. Эллипс

Изучайте различные примеры и задачи по построению эллипсов, чтобы лучше понять и закрепить теоретические знания на практике.