Как использовать Формулу Маклорена для нахождения арксинуса
Формула Маклорена является полезным инструментом в математике для разложения функций в ряд. На этой странице вы найдете подборку фотографий и полезные советы по применению Формулы Маклорена для вычисления арксинуса.
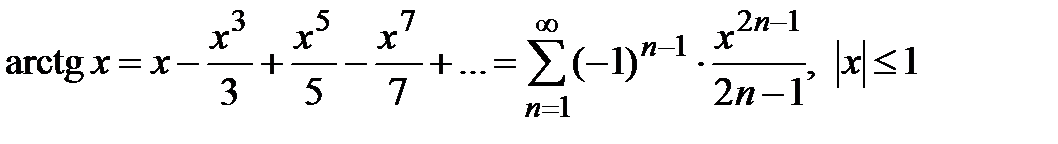

Для нахождения разложения функции арксинуса используйте Формулу Маклорена: arcsin(x) = x + (1/6)x^3 + (3/40)x^5 + ...

Первые несколько членов ряда могут дать достаточно точное приближение для небольших значений x.
Ряд Тейлора и Маклорена на пальцах. Как вычисляет калькулятор?
Для повышения точности используйте больше членов ряда.
11.1 Разложение элементарных функций в ряд Маклорена (часть1)
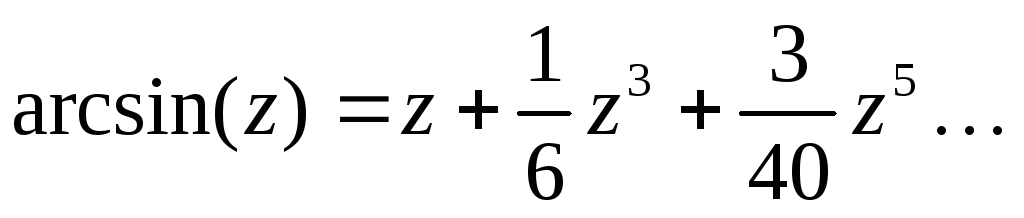

Проверьте радиус сходимости ряда, чтобы гарантировать корректность вычислений.
Для численных вычислений используйте специализированные математические пакеты, такие как Mathematica или MATLAB.


Учтите, что ряд Маклорена для арксинуса сходится медленно для значений x, близких к 1.
Используйте вычислительные методы, такие как алгоритмы оптимизации, для улучшения скорости сходимости.

Изучите примеры разложения других функций с помощью Формулы Маклорена для лучшего понимания процесса.
[Calculus - глава 11] Ряд Тейлора


Обратите внимание на числовые ошибки, возникающие при вычислениях с плавающей точкой.
10. Ряд Тейлора. Ряд Маклорена
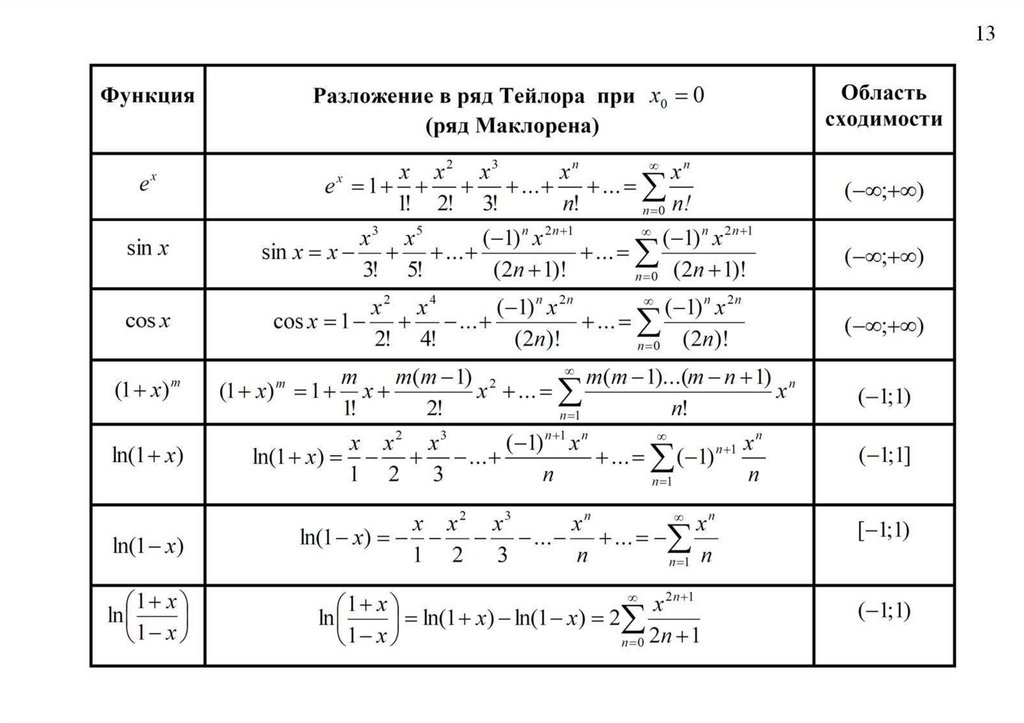

Практикуйтесь в решении задач на разложение функций в ряд, чтобы улучшить свои навыки в этой области.