Понимание формулы обратной пропорциональности и её применения

Формула обратной пропорциональности помогает понять зависимость между двумя величинами, где увеличение одной величины приводит к уменьшению другой. Эта страница предлагает обзор основных принципов и примеров использования этой формулы в различных задачах, что поможет лучше понять и применить её на практике.

Обратная пропорциональность означает, что увеличение одной величины приводит к уменьшению другой. Убедитесь, что вы правильно определяете переменные для корректного применения формулы.

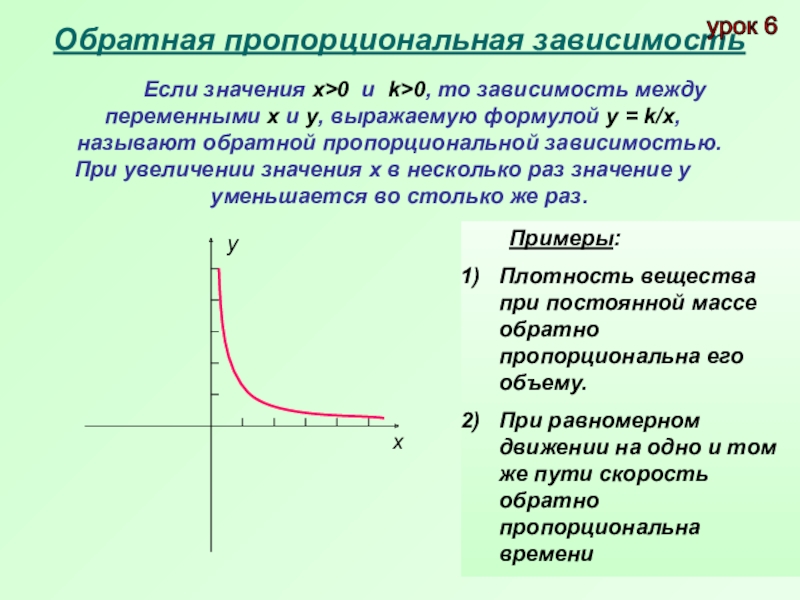
При решении задач с обратной пропорциональностью сначала проверьте, что у вас действительно имеет место такая зависимость между величинами, а не прямая пропорциональность.

Используйте графики для визуализации зависимостей: это поможет лучше понять, как изменение одной величины влияет на другую.

В некоторых случаях может быть полезно создать таблицу значений для обеих величин, чтобы увидеть, как изменение одной из них влияет на другую.

Для проверки правильности решения попробуйте подставить результаты обратно в исходное уравнение и убедитесь, что они соответствуют данным условиям.

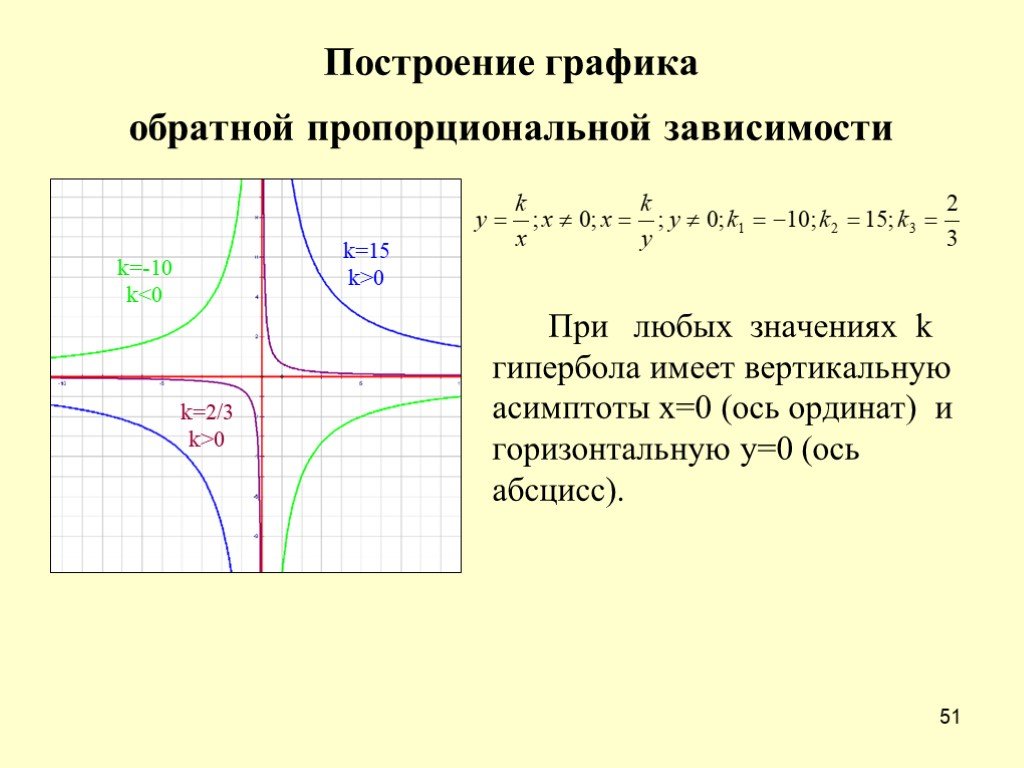
При работе с формулой обратной пропорциональности полезно знать основные математические преобразования и уметь решать дробные уравнения.

Практикуйтесь на различных примерах задач, чтобы уверенно применять формулу в разных ситуациях и типах задач.

Если вам трудно запомнить формулу, попробуйте связать её с реальными примерами из жизни, чтобы лучше понять её применение.

Помните, что для сложных задач с несколькими переменными может потребоваться использование дополнительных методов и подходов для решения уравнений.

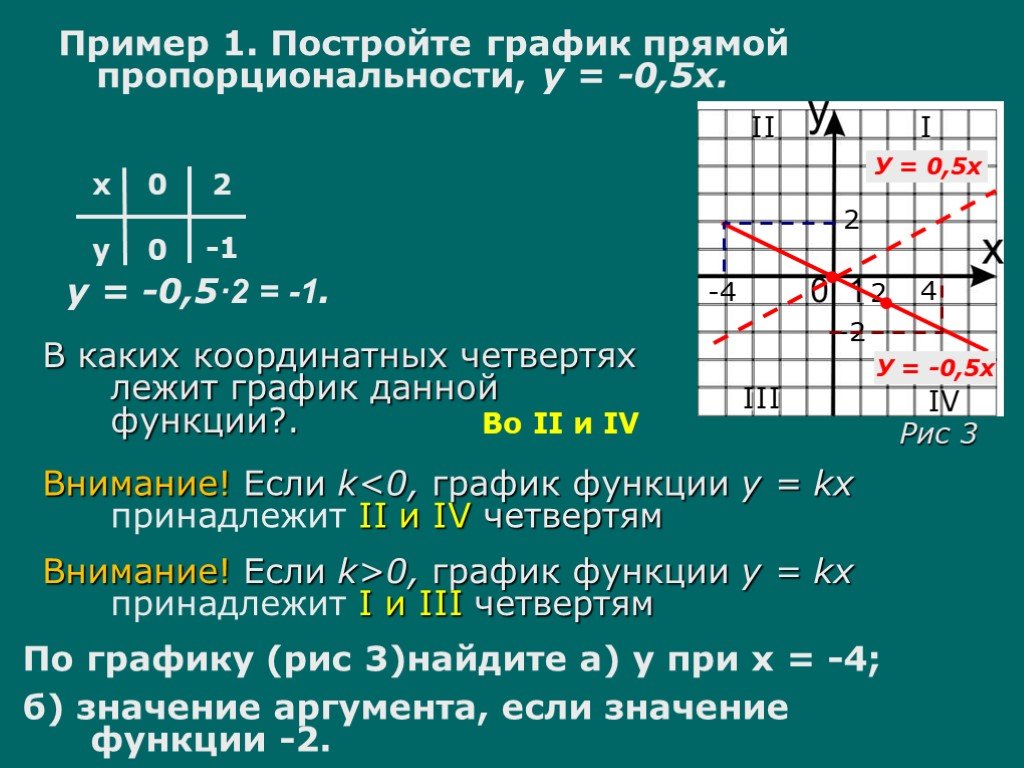
При обучении формуле обратной пропорциональности не забывайте про её связь с другими математическими концепциями, такими как функции и графики.