Как решать систему уравнений: алгоритмы и советы
На этой странице вы найдете подборку фотографий и полезные советы о том, как решать систему уравнений с помощью различных алгоритмов. Пошаговое руководство поможет вам понять и применить методы для достижения верных результатов.
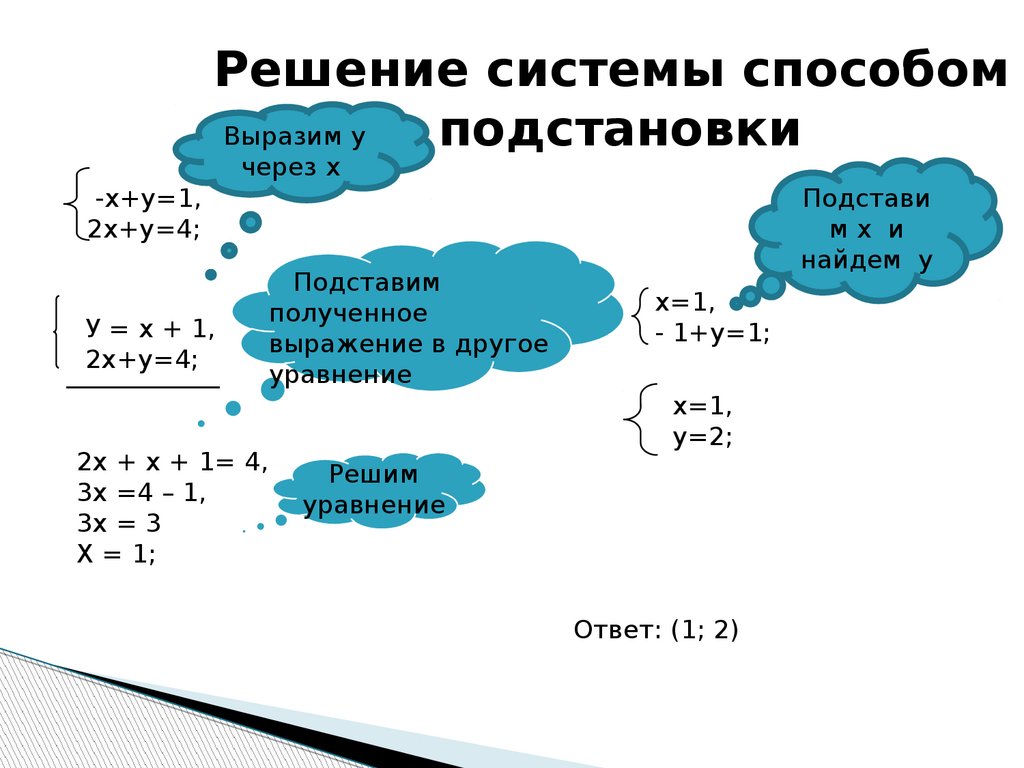

Начните с упрощения уравнений, если это возможно. Упростите выражения и сократите дроби.

Используйте метод подстановки для линейных систем уравнений, чтобы упростить решение.
Решение системы линейных уравнений. Подстановка. С дробными выражениями.

Метод Гаусса можно применять для систем с большим количеством уравнений и неизвестных.
Простенькая задача, которую не решил каждый второй

Не забывайте проверять свои результаты, подставляя их обратно в исходные уравнения.
7 класс, 39 урок, Метод алгебраического сложения


Метод Крамера применим для квадратных систем уравнений и позволяет найти решения с помощью определителей.
ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод Подстановки

Используйте графический метод для наглядного представления и понимания решений линейных систем уравнений.


Метод итераций полезен для нелинейных систем уравнений и приближенного нахождения решений.

Применение символьных вычислений может упростить решение сложных систем уравнений.

Для сложных систем уравнений используйте специализированное программное обеспечение, такое как MATLAB или Mathematica.
Система линейных уравнений. Общее решение. Метод Гаусса

Изучите и применяйте алгоритмы, такие как метод Ньютона-Рафсона, для решения систем нелинейных уравнений.