Изучаем формулы комбинаторики: сочетания с повторениями

Комбинаторика — важный раздел математики, который помогает понимать, как можно создавать различные комбинации элементов. В этой статье рассмотрим формулы для сочетаний с повторами, дадим полезные советы и покажем примеры использования.

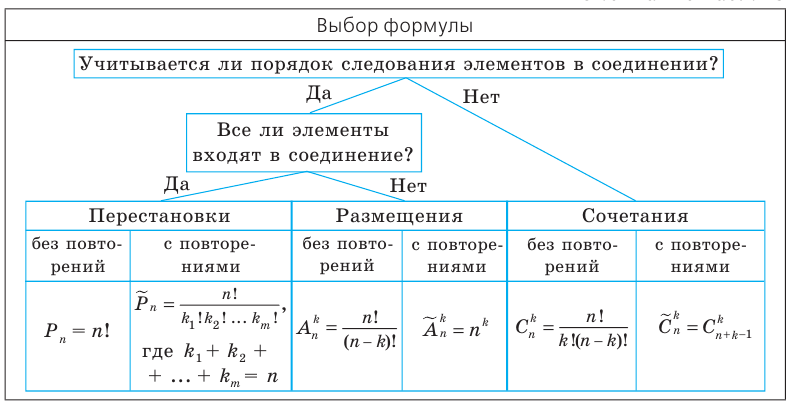
Прежде чем приступать к задачам на сочетания с повторами, важно понять основные принципы комбинаторики и различия между пермутациями, сочетаниями и размещениями.

Используйте формулу сочетаний с повторами: C(n + k - 1, k) = (n + k - 1)! / (k! (n - 1)!), где n — количество элементов, а k — количество выбираемых элементов.

Начинайте с простых задач, чтобы закрепить понимание основных принципов и формул, постепенно переходя к более сложным.

Практикуйте решение задач с использованием разных источников, таких как учебники, онлайн-курсы и математические сообщества.

Создавайте собственные задачи и пытайтесь решать их, чтобы глубже понять материал и улучшить навыки.

Используйте графические представления, такие как деревья решений или диаграммы Венна, чтобы визуализировать сочетания и упрощать понимание задач.

Записывайте и анализируйте свои решения, чтобы видеть прогресс и находить ошибки, которые можно исправить.

Не бойтесь обращаться за помощью к преподавателям или коллегам, если сталкиваетесь с трудностями в понимании материала.

Регулярно повторяйте изученный материал, чтобы закрепить знания и навыки на длительный срок.

Используйте программные инструменты и калькуляторы для проверки своих решений и ускорения процесса вычислений.