Как использовать косинус острого угла в прямоугольном треугольнике
В этом разделе мы рассмотрим косинус острого угла прямоугольного треугольника, его свойства и применение в задачах геометрии. Вы узнаете, как правильно вычислять косинус и применять его для решения различных математических задач.
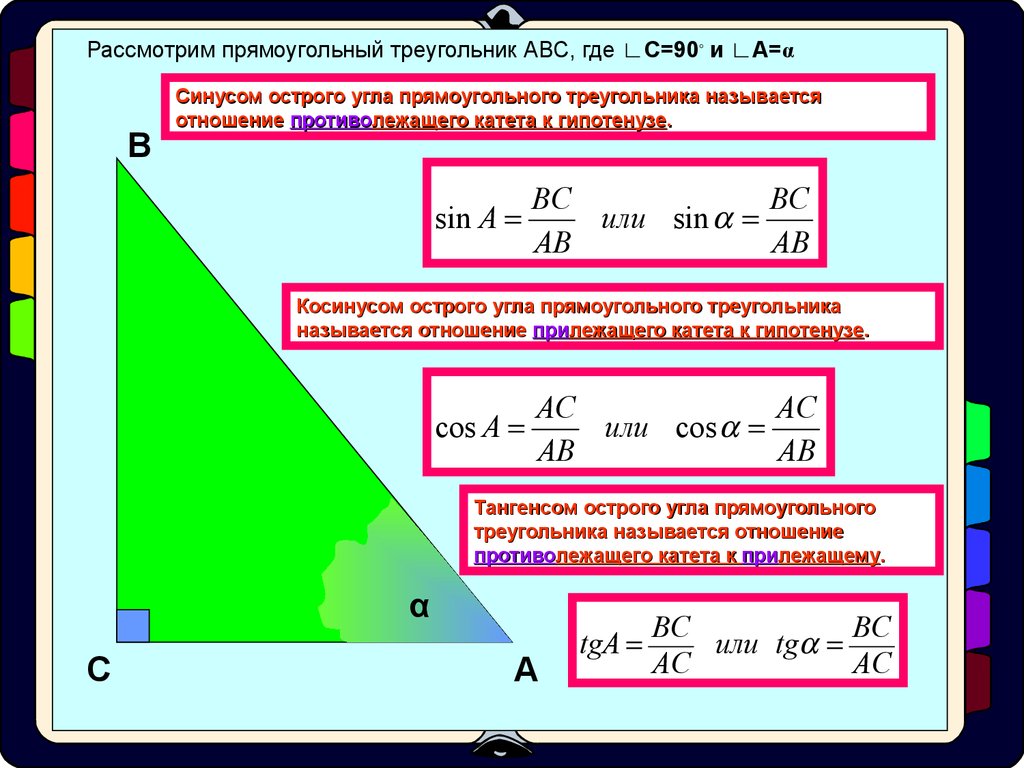
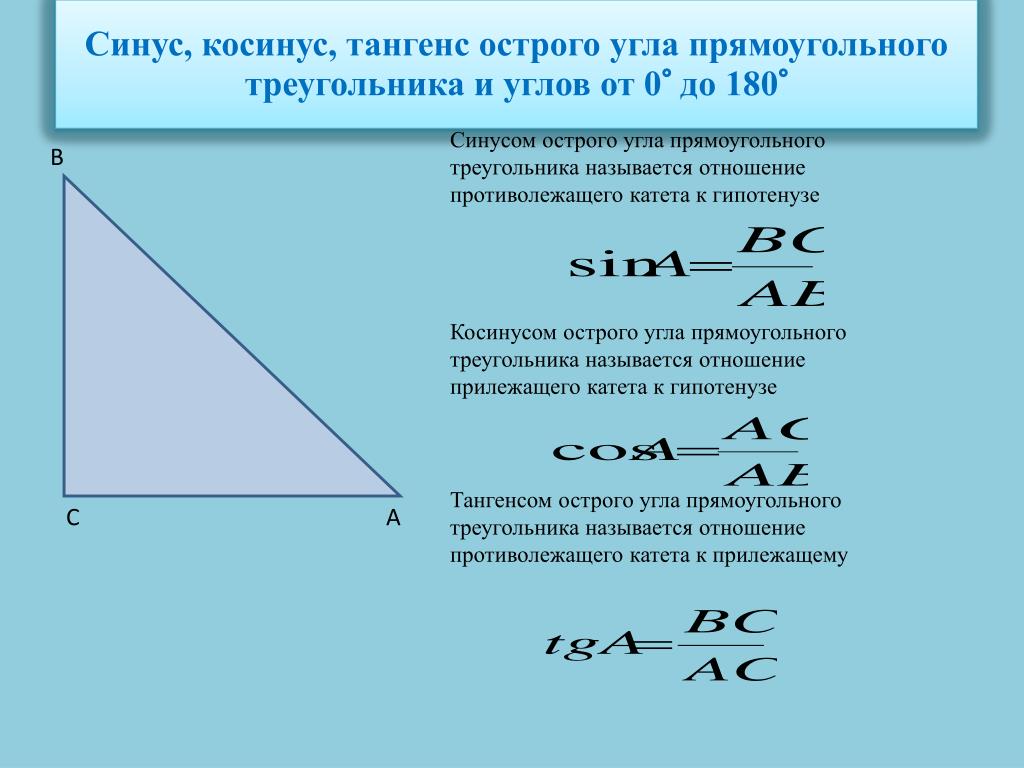

Изучите основные тригонометрические функции: синус, косинус и тангенс.
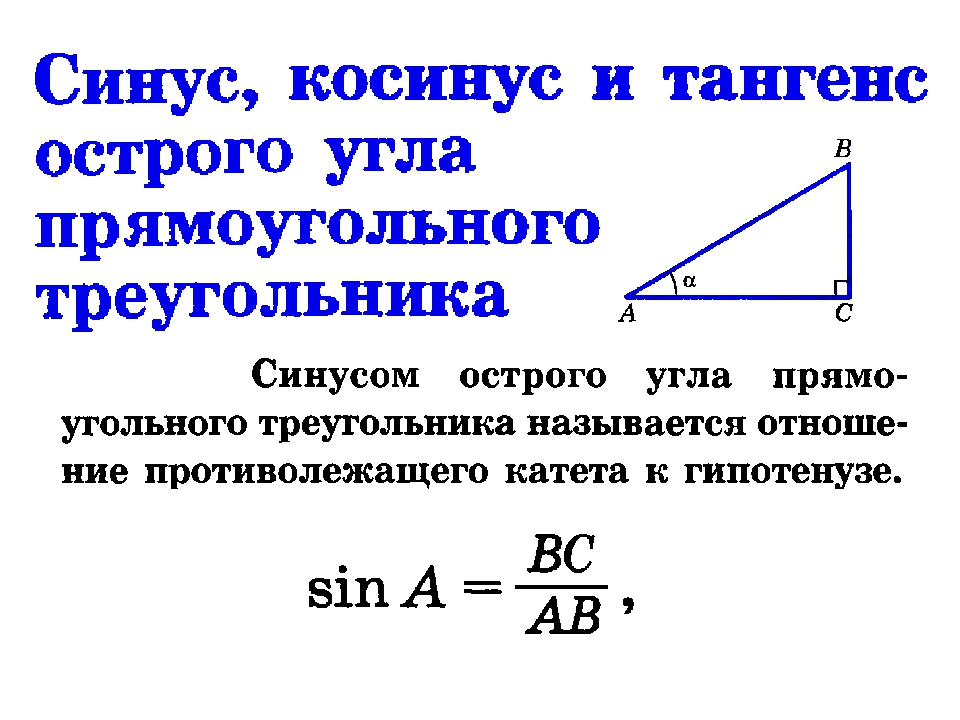
8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольника

Понимайте, что косинус острого угла равен отношению прилежащего катета к гипотенузе.
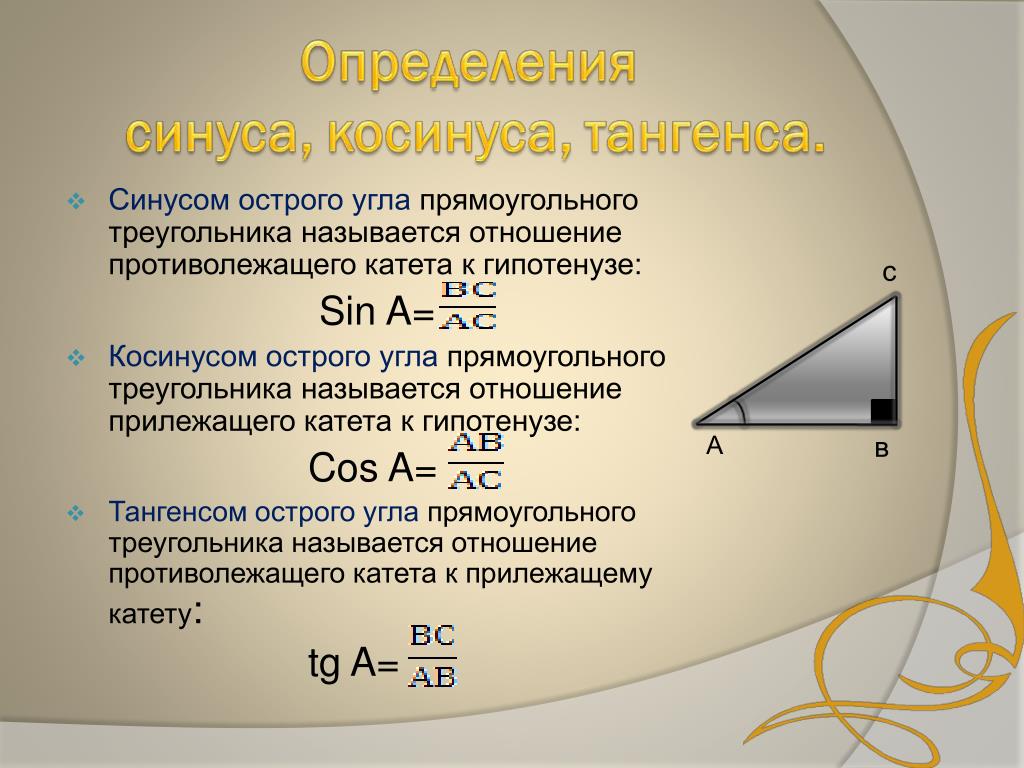
Используйте единичную окружность для визуализации тригонометрических функций.
ТРИГОНОМЕТРИЯ - Синус, Косинус, Тангенс, Котангенс
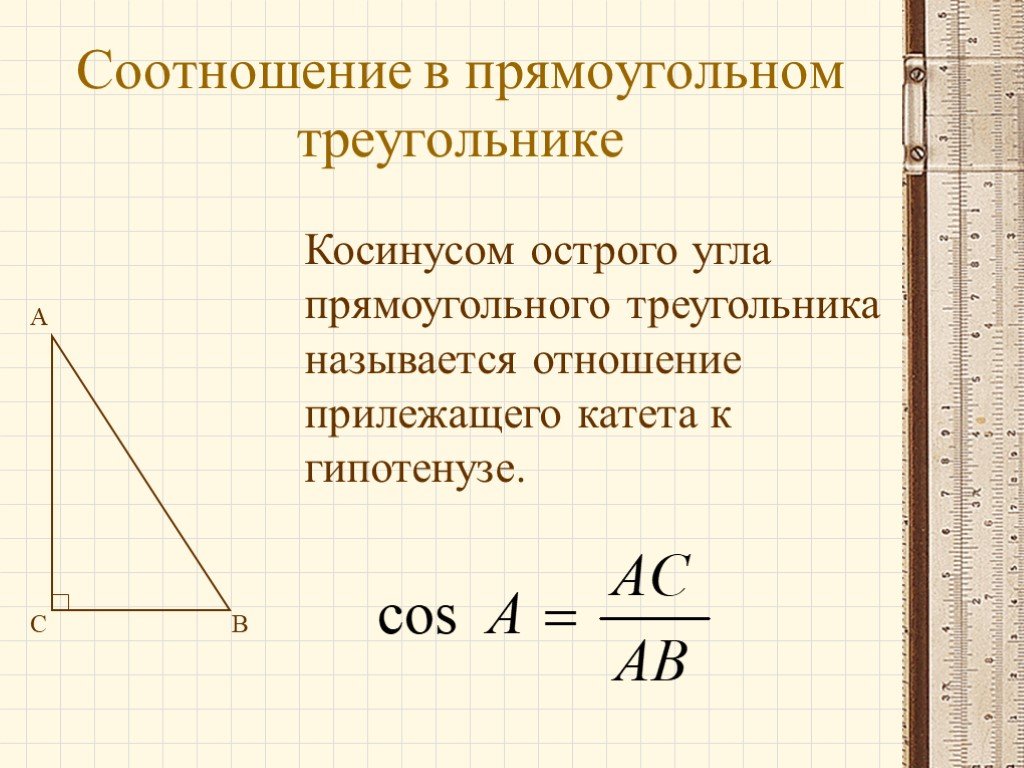
Запомните основные значения косинуса для углов 30°, 45° и 60°.
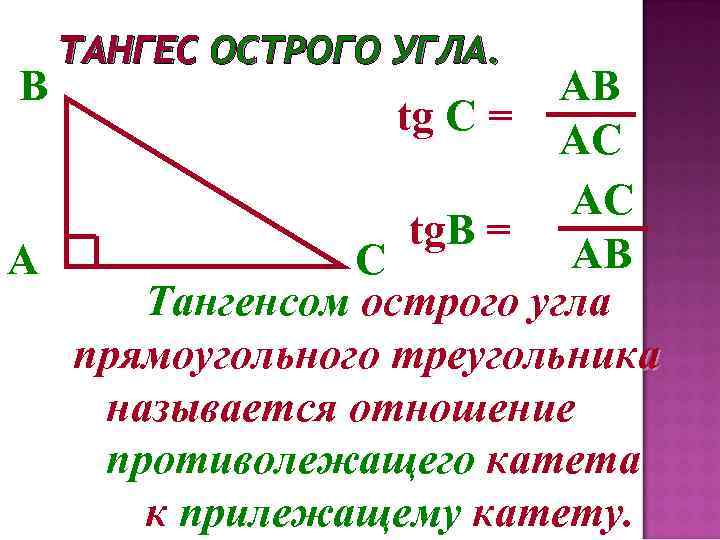
Применяйте теорему Пифагора для нахождения длин сторон треугольника.
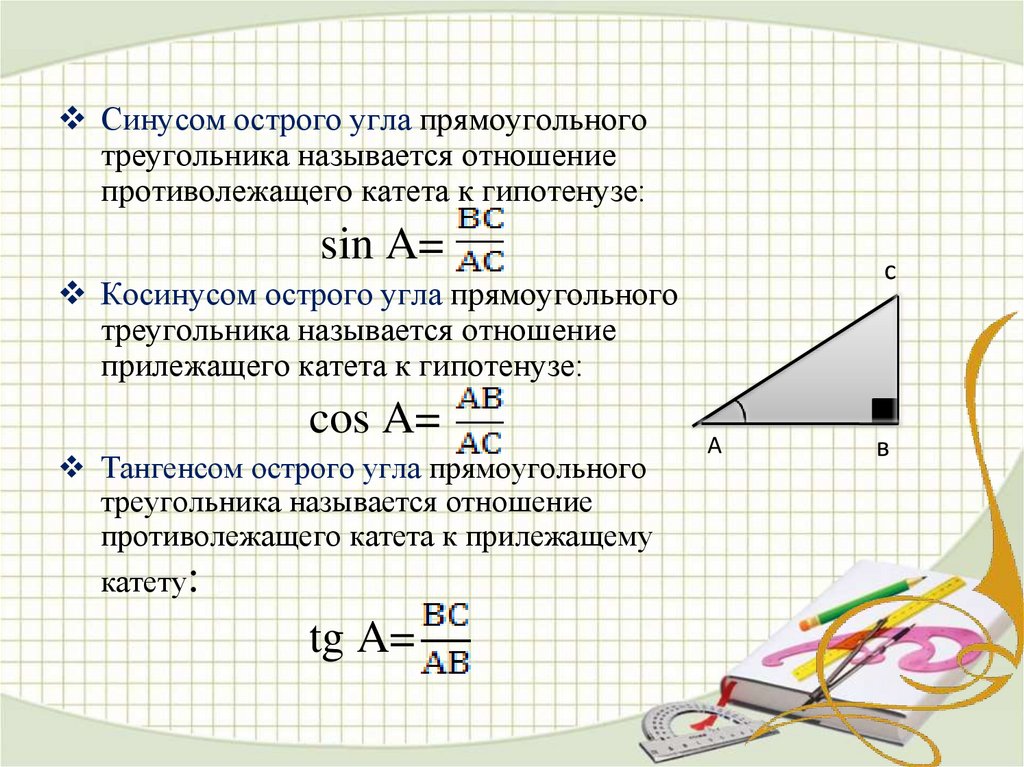
Регулярно решайте задачи на нахождение косинуса для закрепления знаний.

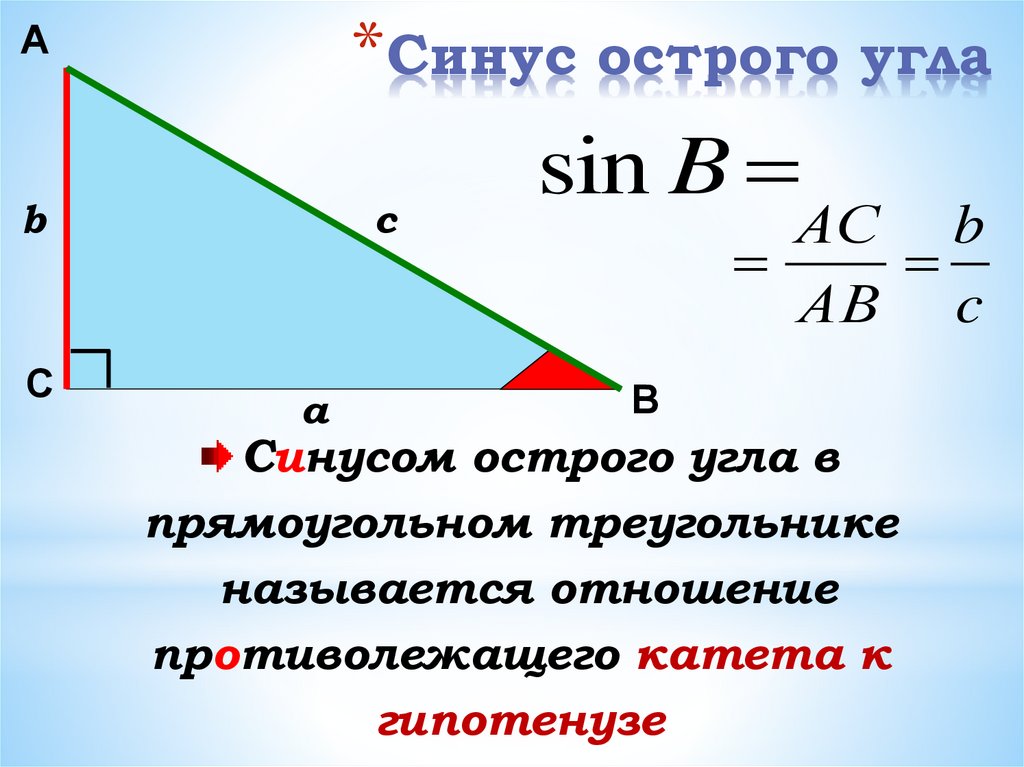
Используйте таблицы значений тригонометрических функций для упрощения расчетов.
Проверяйте свои вычисления с помощью калькулятора.
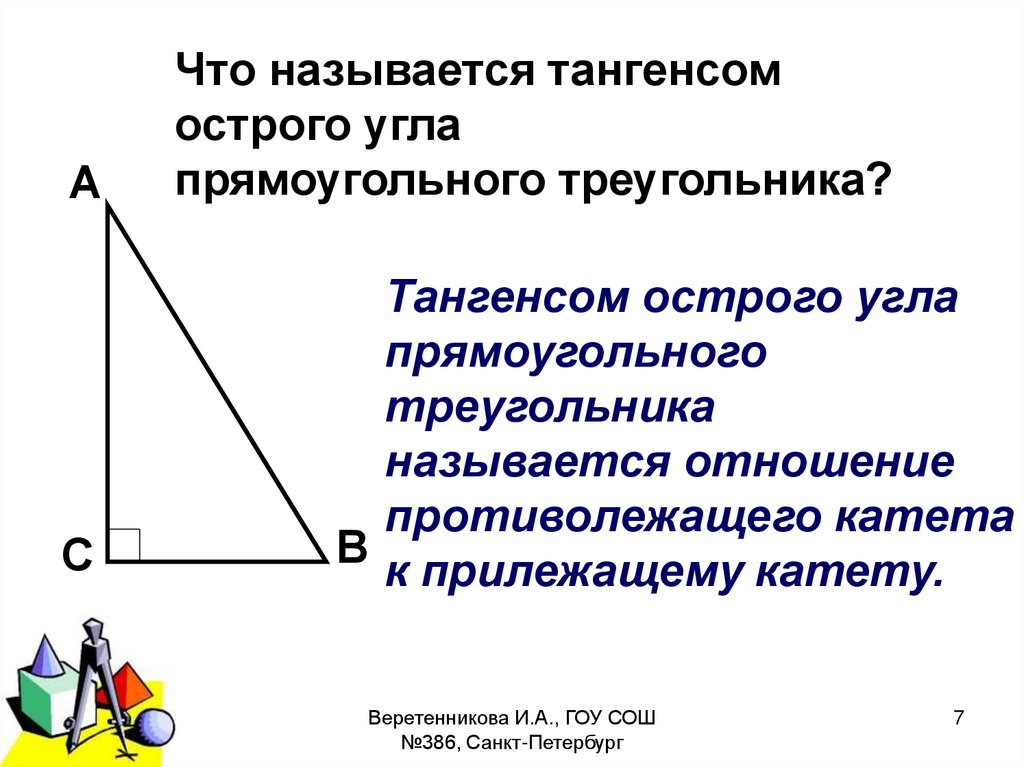

Практикуйтесь в решении задач на нахождение углов по известным сторонам треугольника.
Синус, косинус и тангенс острого угла прямоуг. треугольника - Геометрия 7-9 класс #66 - Инфоурок
Используйте графики тригонометрических функций для лучшего понимания их поведения.