Как использовать медианы треугольника для решения задач
Медианы треугольника играют важную роль в геометрии, они соединяют вершину треугольника с серединой противоположной стороны и пересекаются в одной точке, называемой центроидом. Эта страница предлагает подборку фотографий и полезных советов по медианам треугольника ABC.
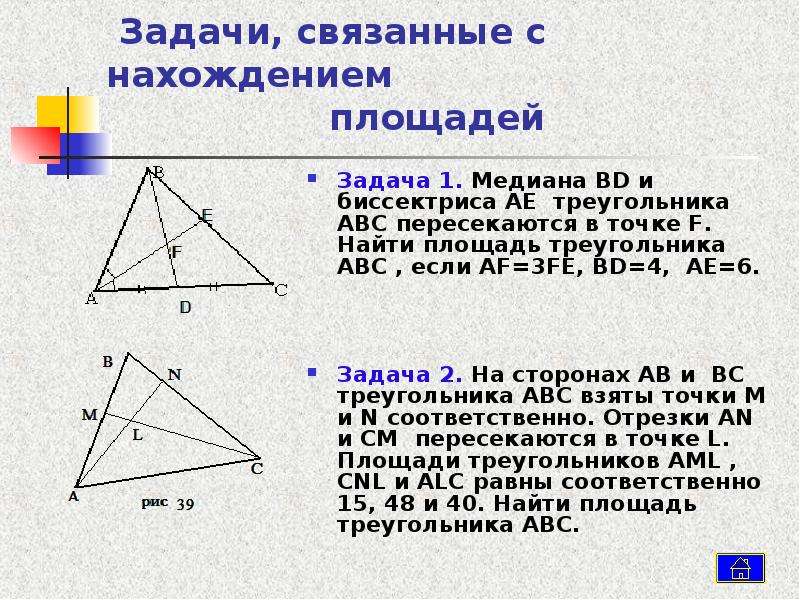

Используйте медианы для нахождения центра тяжести треугольника.
№807. Пусть AA1, ВВ1 и СС1 — медианы треугольника ABC, О — произвольная точка. Докажите, что ОА + ОВ
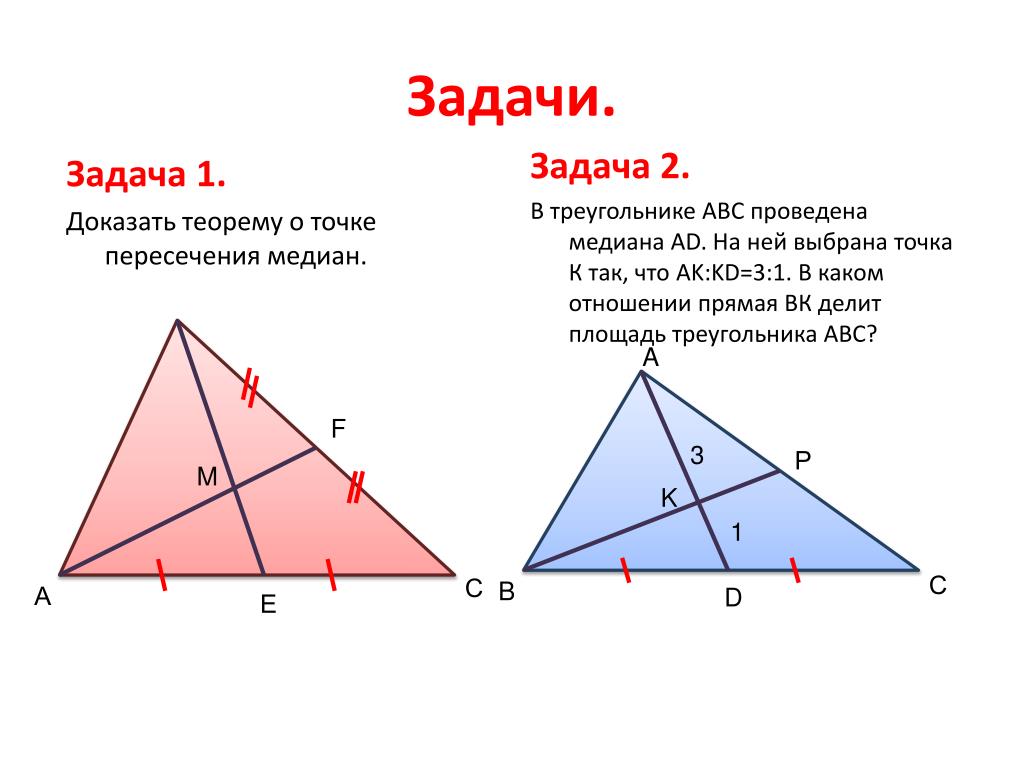
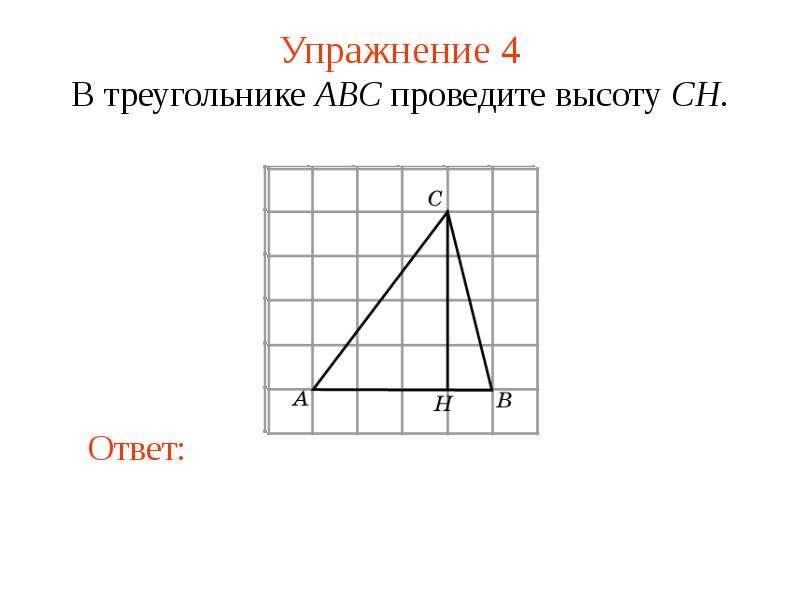
Запомните, что медианы треугольника пересекаются в одной точке, деля его на шесть равных по площади частей.
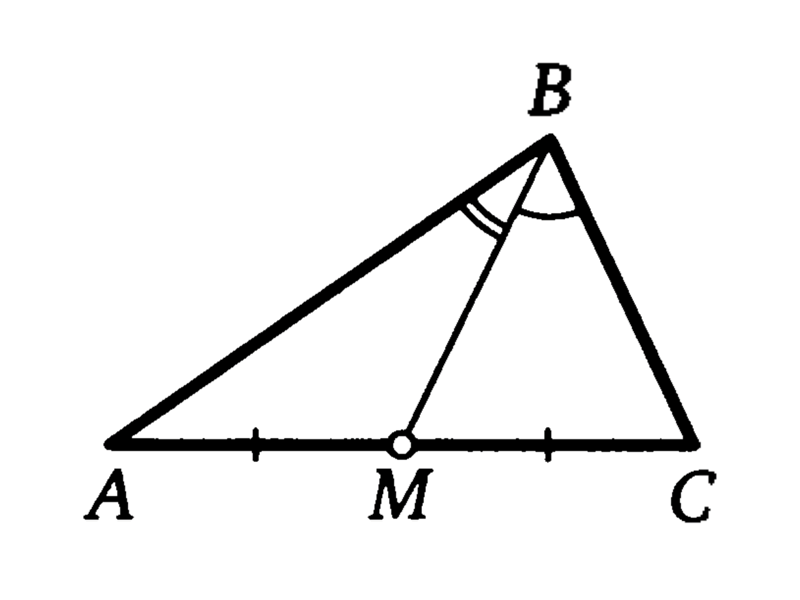

Медианы треугольника всегда пересекаются в соотношении 2:1, считая от вершины.
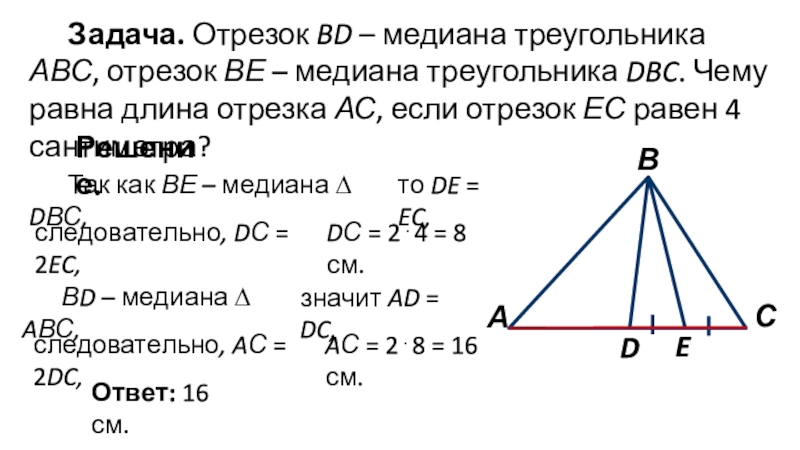

При решении задач на координатной плоскости медианы можно использовать для нахождения координат центроида.
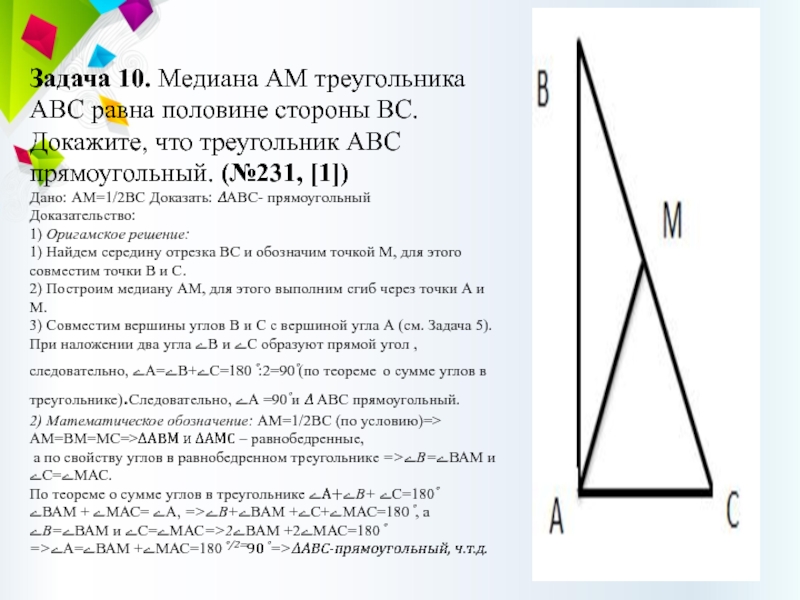
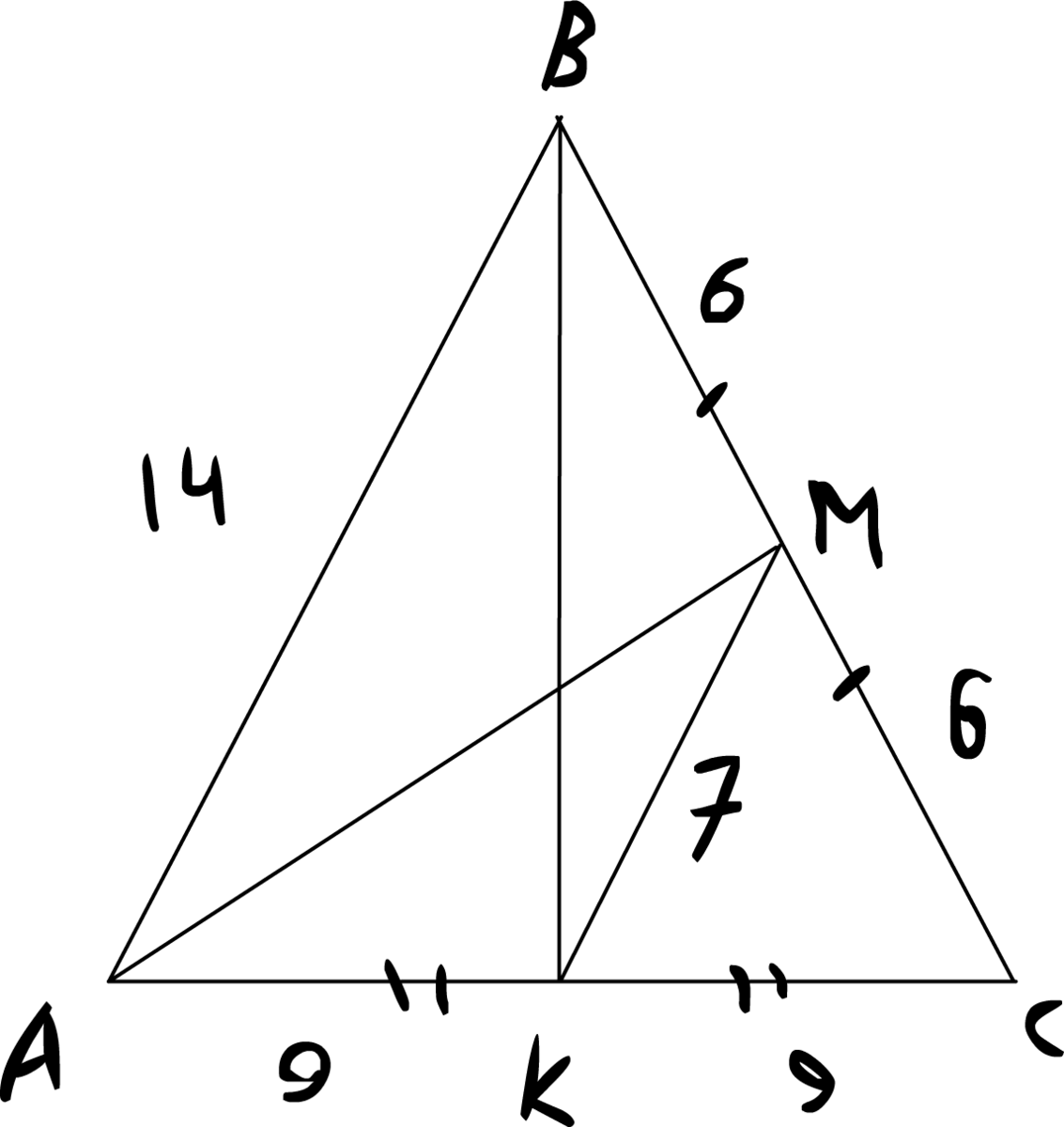
Если все стороны треугольника известны, длину медианы можно вычислить с помощью формулы медианы.
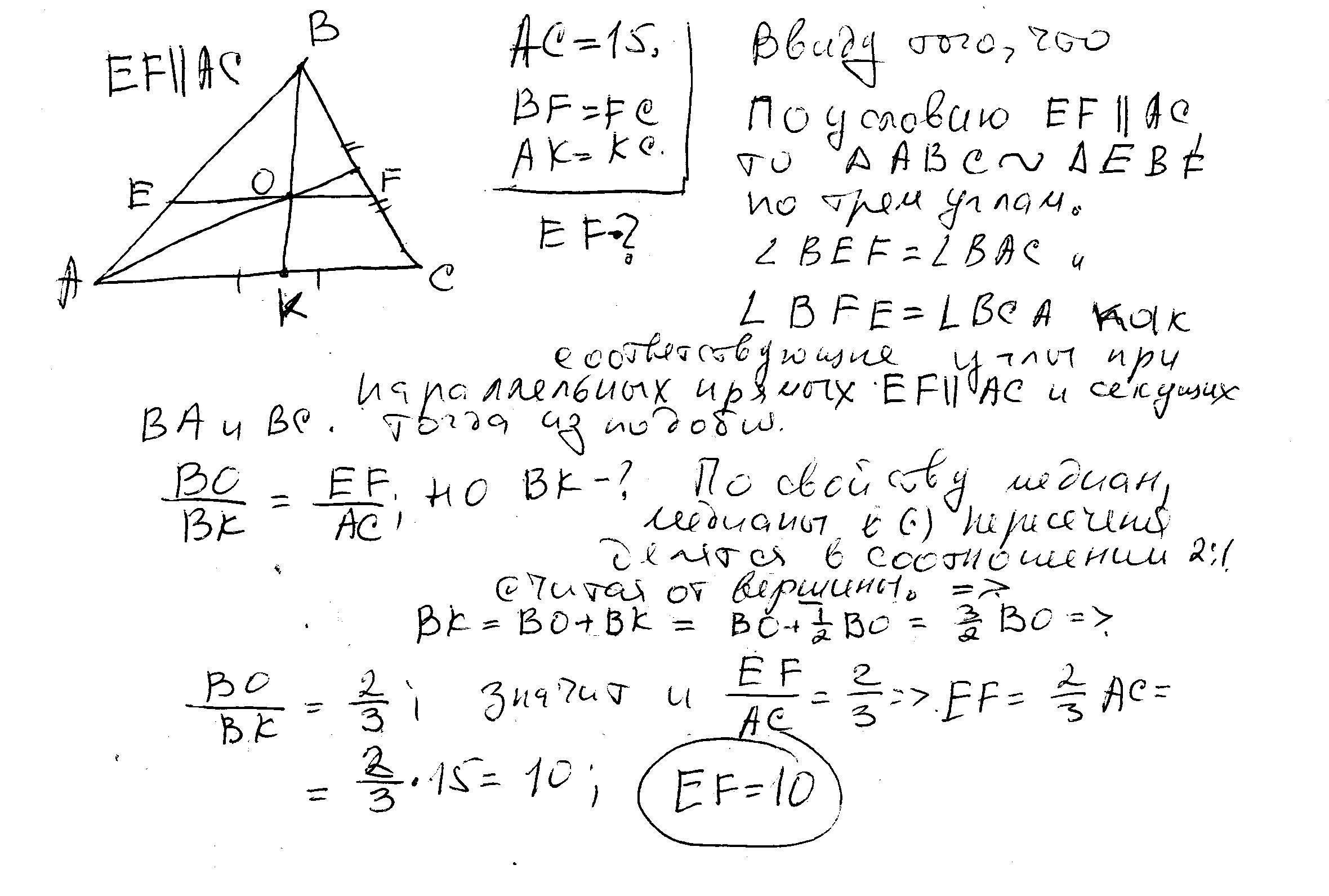
Запомните, что медианы делят треугольник на три пары равновеликих треугольников.

Используйте медианы для проверки правильности решения задач на нахождение сторон и углов треугольника.
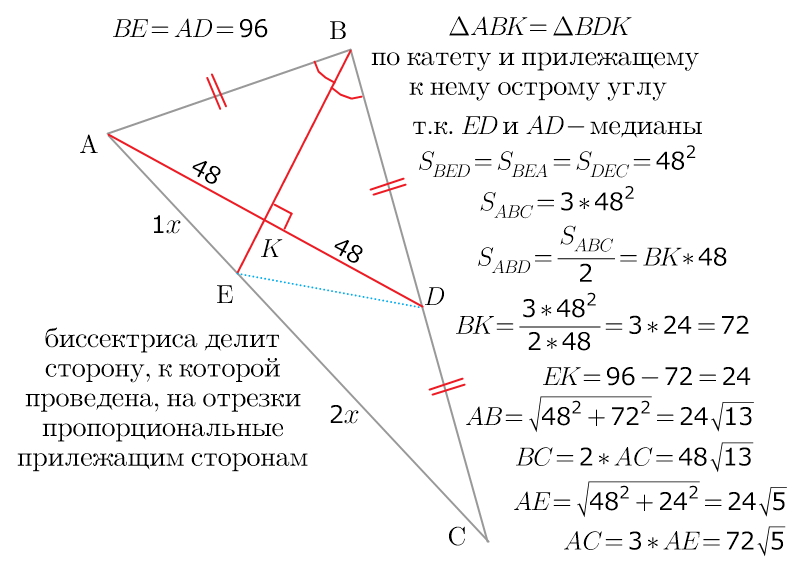
Медианы треугольника могут быть полезны при решении задач на построение.
Помните, что медиана равнобедренного треугольника, проведенная к основанию, также является биссектрисой и высотой.
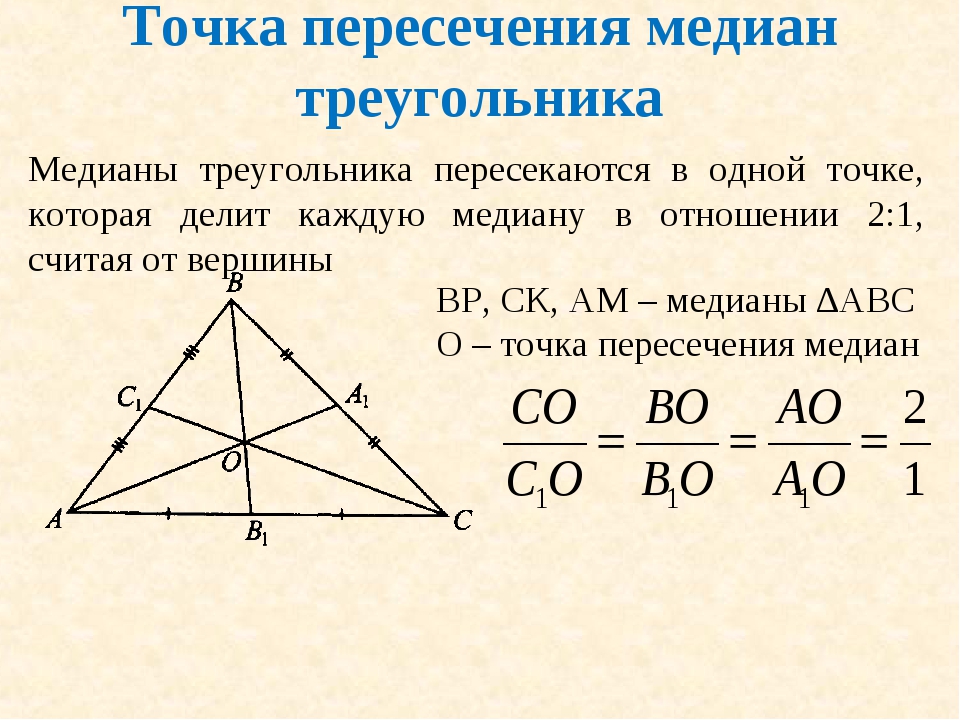
Медианы могут помочь в доказательствах геометрических теорем и утверждений.