Преимущества метода флюксий Ньютона в математике
Метод флюксий Ньютона — это мощный инструмент, используемый в математике для нахождения производных функций. Этот метод играет ключевую роль в анализе изменения величин и используется для решения широкого спектра задач.


Начните с изучения основ дифференциального исчисления, чтобы понять, как работает метод флюксий Ньютона.


Практикуйте решение простых задач с использованием метода флюксий, чтобы укрепить свои навыки.

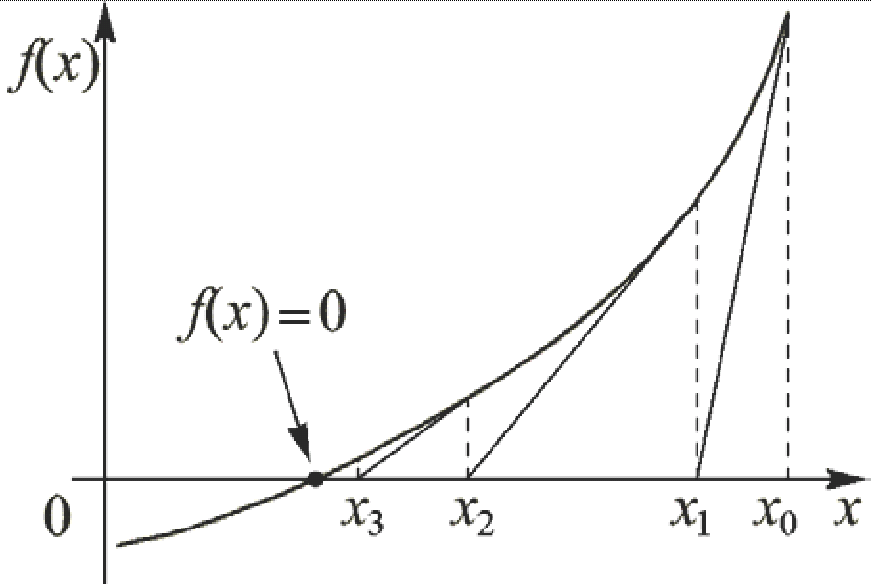
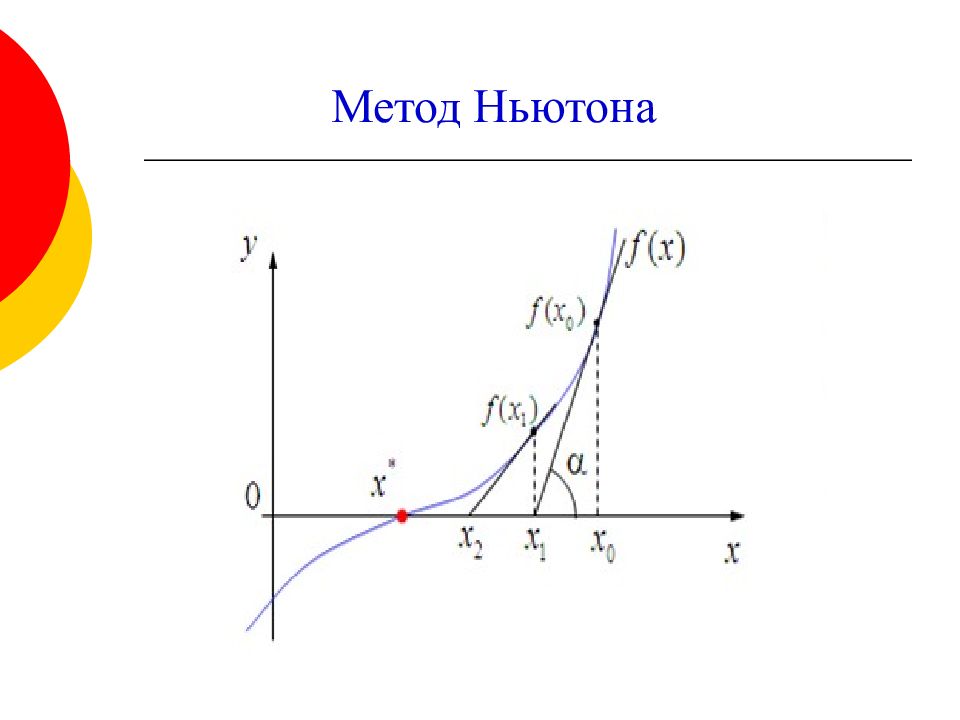
Используйте графическое представление функций, чтобы визуализировать процесс нахождения производных.


Применяйте метод флюксий Ньютона в сочетании с другими математическими техниками для более эффективного решения сложных задач.
Что такое и как применять метод Ньютона? Душкин объяснит


Регулярно решайте задачи из учебников и онлайн-ресурсов, чтобы улучшить свои навыки.


Консультируйтесь с преподавателями или коллегами, чтобы получить обратную связь и улучшить свои методы решения задач.

Используйте программные инструменты для проверки своих решений и автоматизации вычислений.

Читайте научные статьи и исследования, чтобы быть в курсе последних достижений в области применения метода флюксий Ньютона.

Учите и применяйте метод флюксий Ньютона в реальных проектах и исследованиях для приобретения практического опыта.
Не бойтесь экспериментировать с различными подходами и техниками, чтобы найти наиболее эффективные методы решения задач.