Как применять метод интервалов при решении неравенств
Метод интервалов является мощным инструментом в математике, позволяющим эффективно решать неравенства. В этой статье вы найдете подборку фотографий, иллюстрирующих данный метод, а также полезные советы по его применению.


Начинайте с определения нулей функции, решая уравнение, приравняв его к нулю.
Решение неравенства методом интервалов

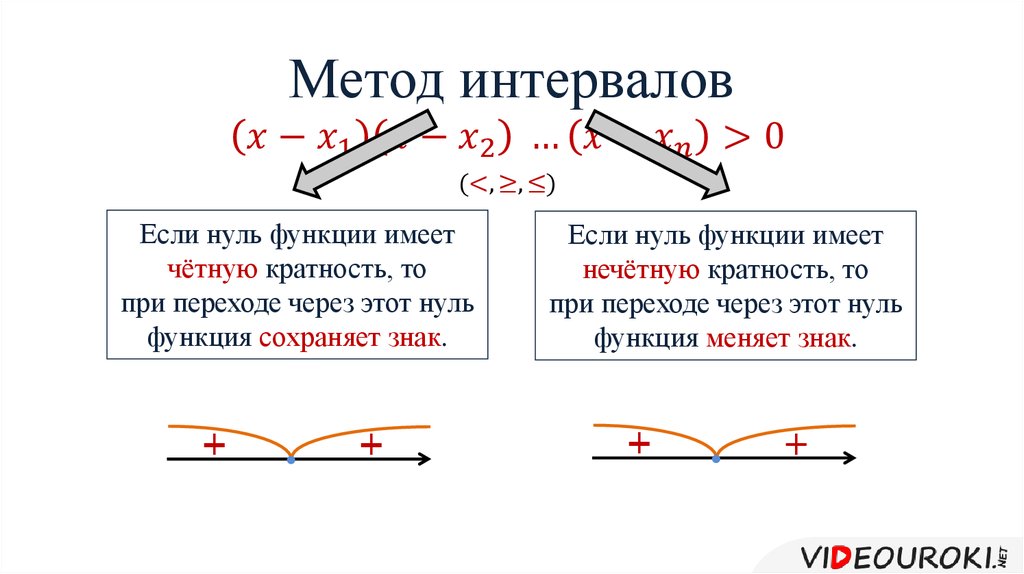
Разделите числовую прямую на интервалы, используя найденные нули.
Что такое Метод интервалов? для Чайников Урок 17.1

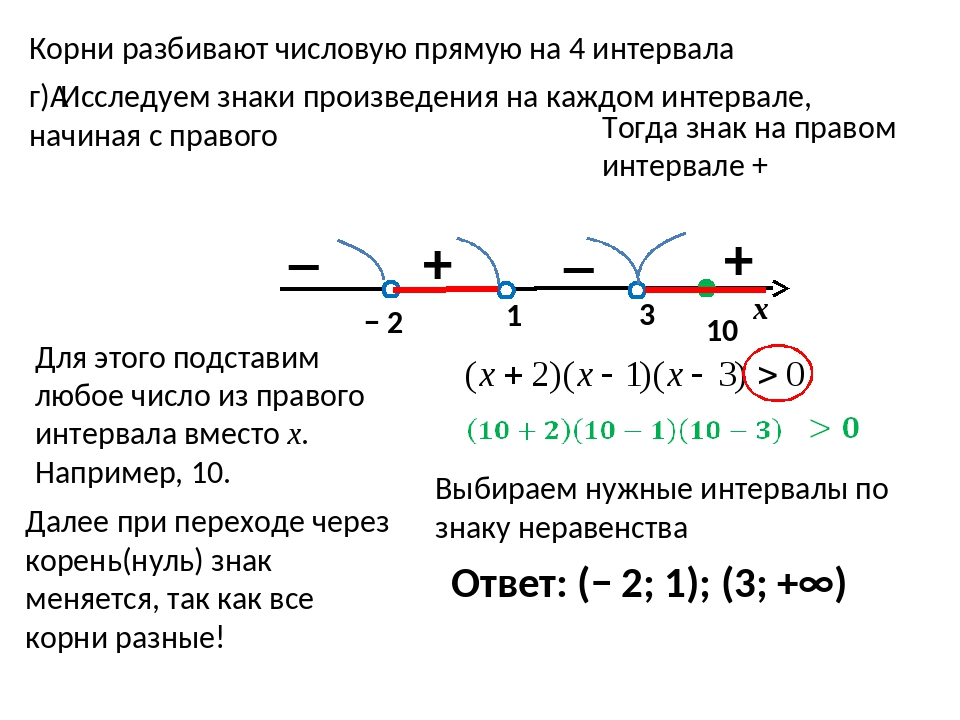
Проверьте знак функции на каждом интервале, подставляя любые значения из интервала в исходное неравенство.
Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные факты


Не забывайте учитывать знак коэффициента перед переменной при проверке знака на интервалах.
Метод интервалов. Простой способ решения неравенств.

Используйте графическое представление для более наглядного понимания интервалов и знаков.
Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства - TutorOnline

При решении рациональных неравенств учитывайте особые точки, где знаменатель равен нулю.

Проверяйте решение, подставляя крайние значения интервалов в исходное неравенство.

Используйте метод интервалов для проверки решений сложных уравнений и неравенств.
УНИВЕРСАЛЬНЫЙ МЕТОД при решении Неравенств — Метод Интервалов

Применяйте метод интервалов в сочетании с другими методами для достижения наилучшего результата.

Практикуйтесь на различных примерах, чтобы лучше понимать и запоминать методику.