Как читать и анализировать графики функций первообразных
Эта страница содержит подборку фотографий и полезные советы по пониманию и анализу графиков функций первообразных. Узнайте, как интерпретировать эти графики и какие методы использовать для их исследования.

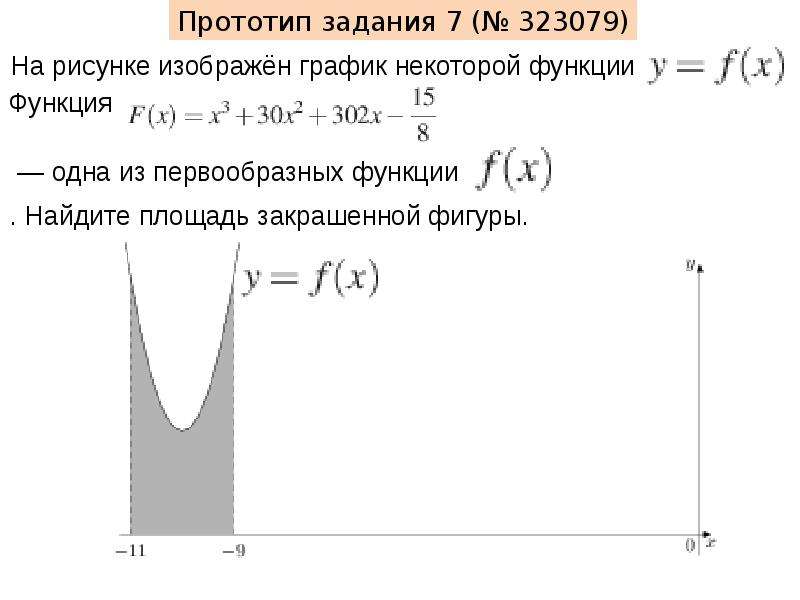
Начните с изучения основных понятий: что такое первообразная и как она связана с исходной функцией.
11 класс, 20 урок, Первообразная и неопределённый интеграл
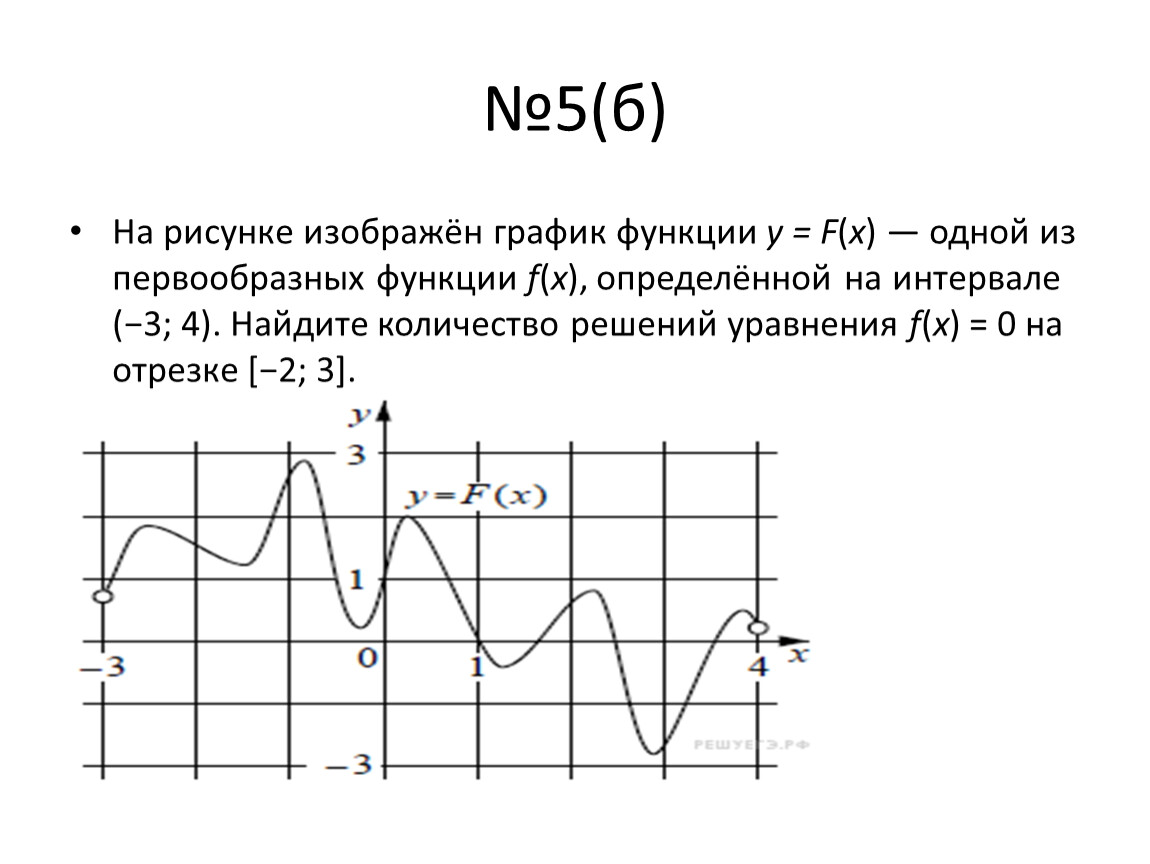
Изучите стандартные формы графиков функций и их первообразных, чтобы легче понимать изменения и тенденции.

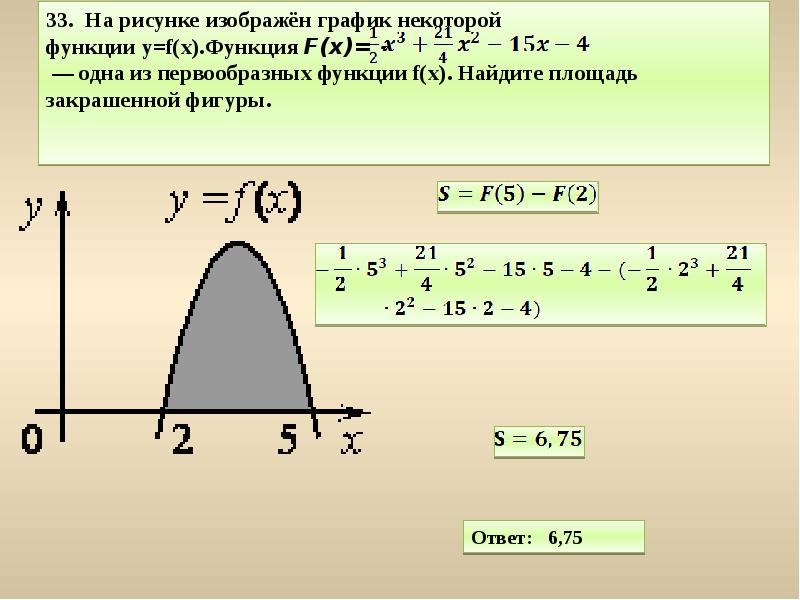
Используйте графические калькуляторы или специализированное программное обеспечение для построения графиков функций первообразных.
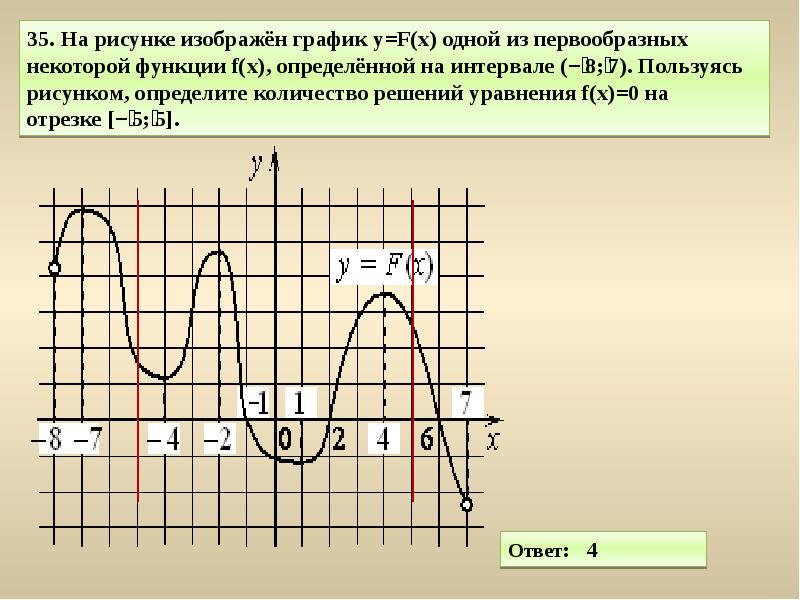

Практикуйтесь на простых примерах, таких как линейные или квадратичные функции, чтобы закрепить понимание.
Задача 7 ЕГЭ на производную и первообразную #29


Обращайте внимание на точки пересечения оси абсцисс, так как они могут быть ключевыми моментами для анализа.
Первообразная. 11 класс.
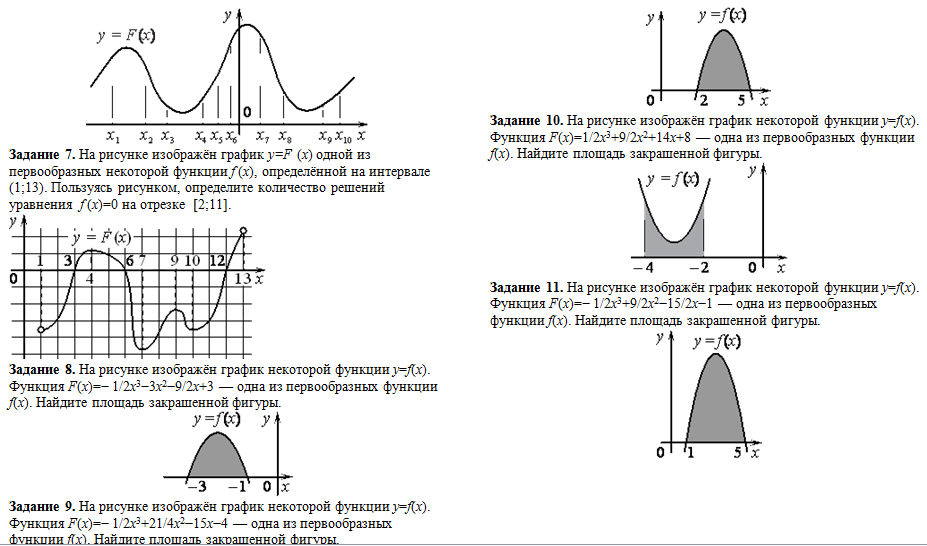

Используйте цветные маркеры или различные стили линий для выделения важных частей графика.

Применяйте методы численного интегрирования для более сложных функций, если аналитические методы затруднительны.
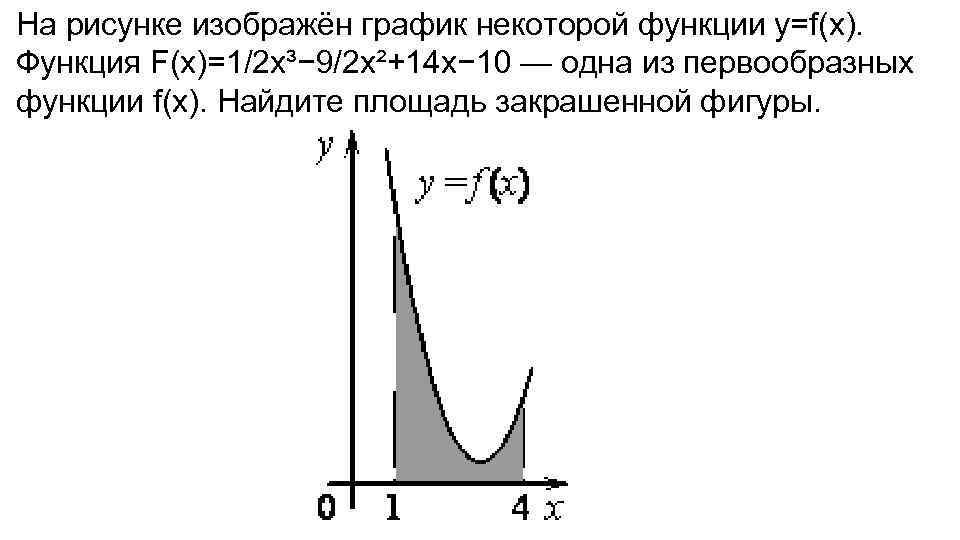
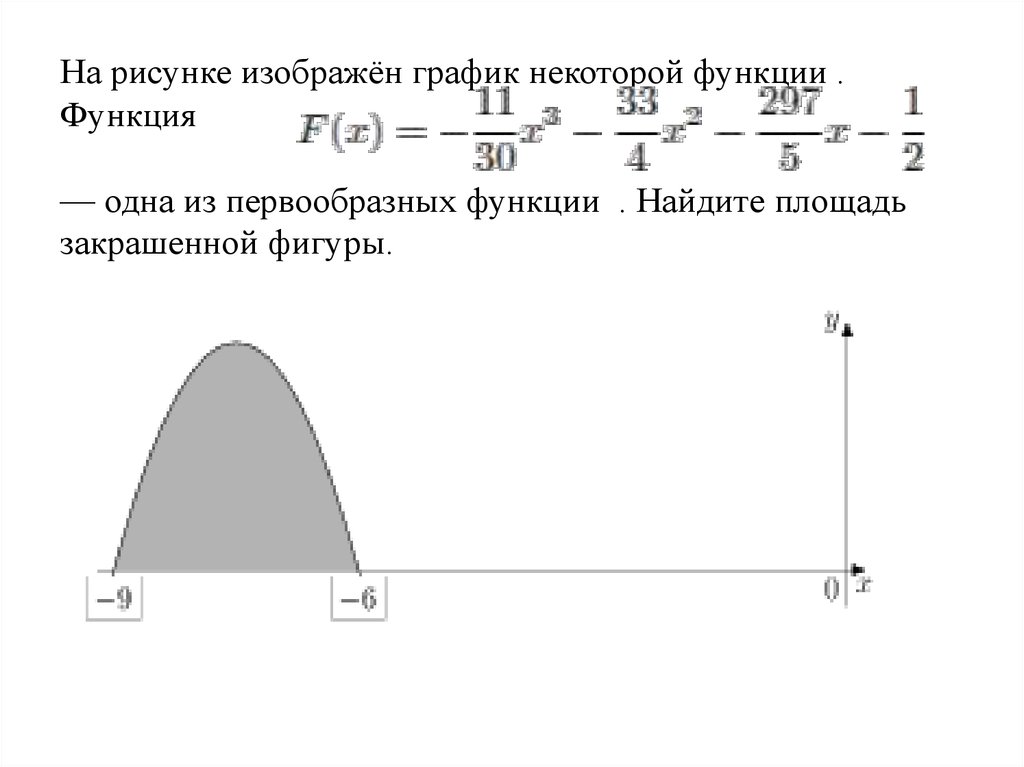
Не забывайте проверять результаты на логичность и соответствие исходным данным.
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x).
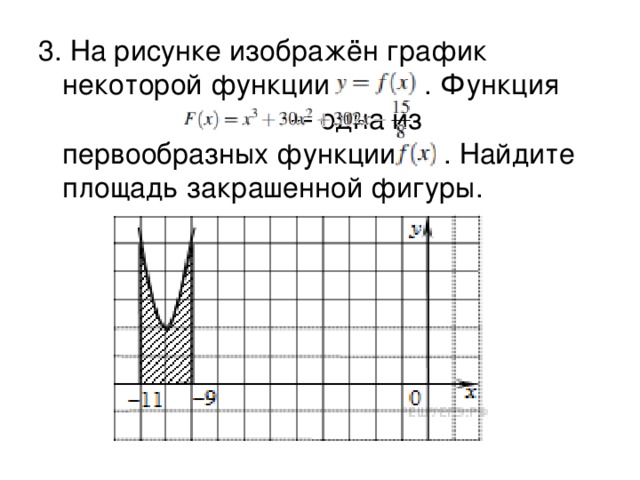
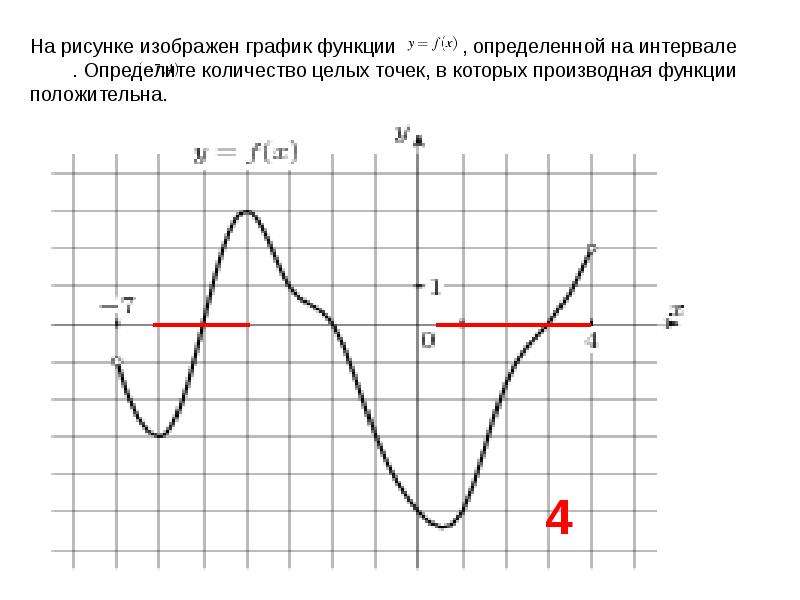
Сравнивайте графики первообразной и исходной функции для лучшего понимания взаимосвязи между ними.
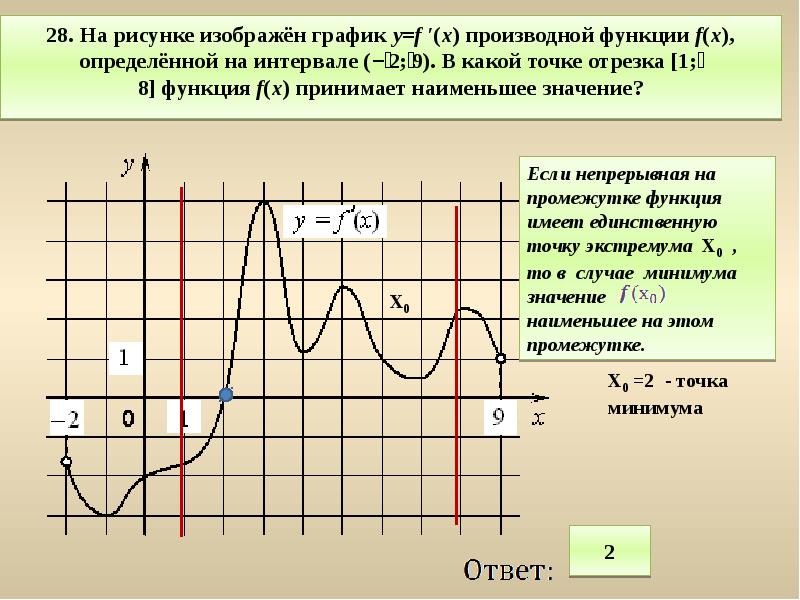
Изучайте литературу и дополнительные ресурсы по теме, чтобы углубить свои знания и навыки анализа графиков функций первообразных.