Пошаговое руководство по нахождению уравнения касательной к графику функции

На этой странице вы найдете полезные советы и примеры по нахождению уравнения касательной к графику функции. Здесь представлены методы и техники, которые помогут вам лучше понять и применить этот математический процесс.

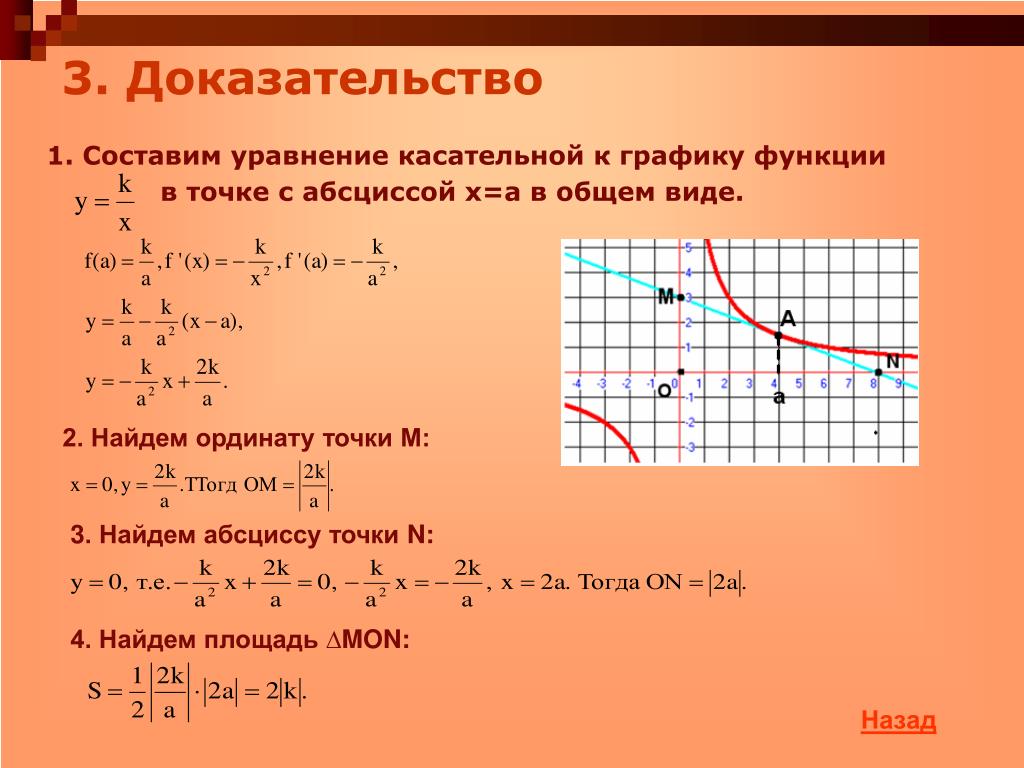
Начните с нахождения производной функции, так как она представляет собой наклон касательной линии в любой точке графика.

Определите точку, в которой вы хотите найти касательную, и подставьте ее в производную, чтобы найти значение наклона.

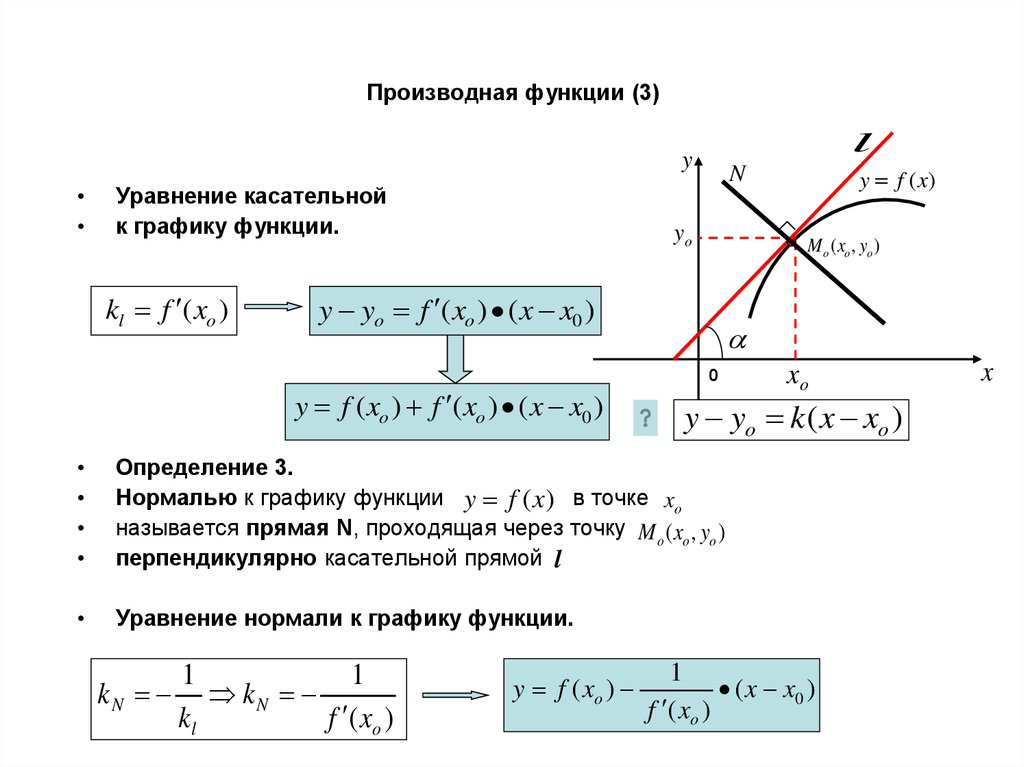
Используйте уравнение прямой линии: y = mx + b, где m — это наклон, найденный с помощью производной.

Подставьте координаты точки в уравнение y = mx + b, чтобы найти значение b — это пересечение касательной с осью y.

Запишите окончательное уравнение касательной, используя найденные значения m и b.

Проверьте свои расчеты, подставив исходную точку в уравнение касательной, чтобы убедиться в правильности результата.

Если функция сложная, рассмотрите возможность упрощения перед дифференцированием.

Используйте графические калькуляторы или компьютерные программы для визуализации касательной и проверки результата.

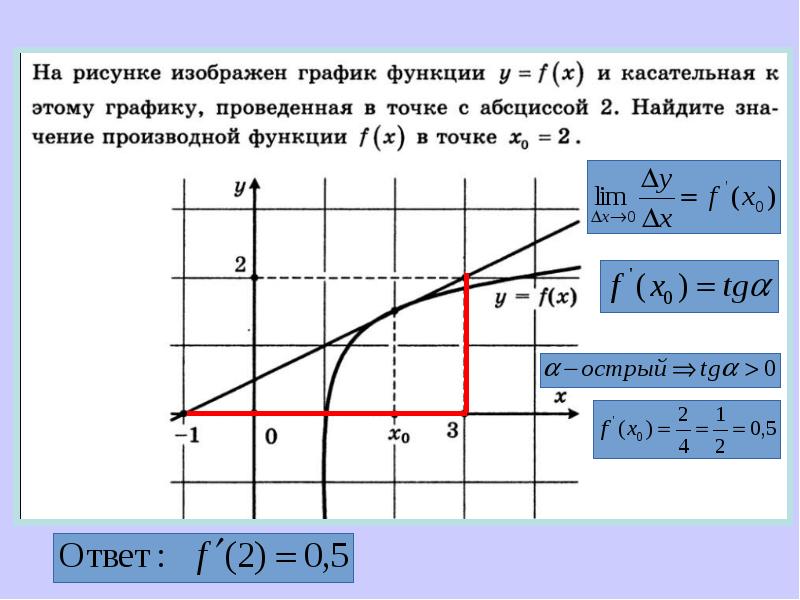
Изучите примеры решения задач на нахождение касательных к различным типам функций.

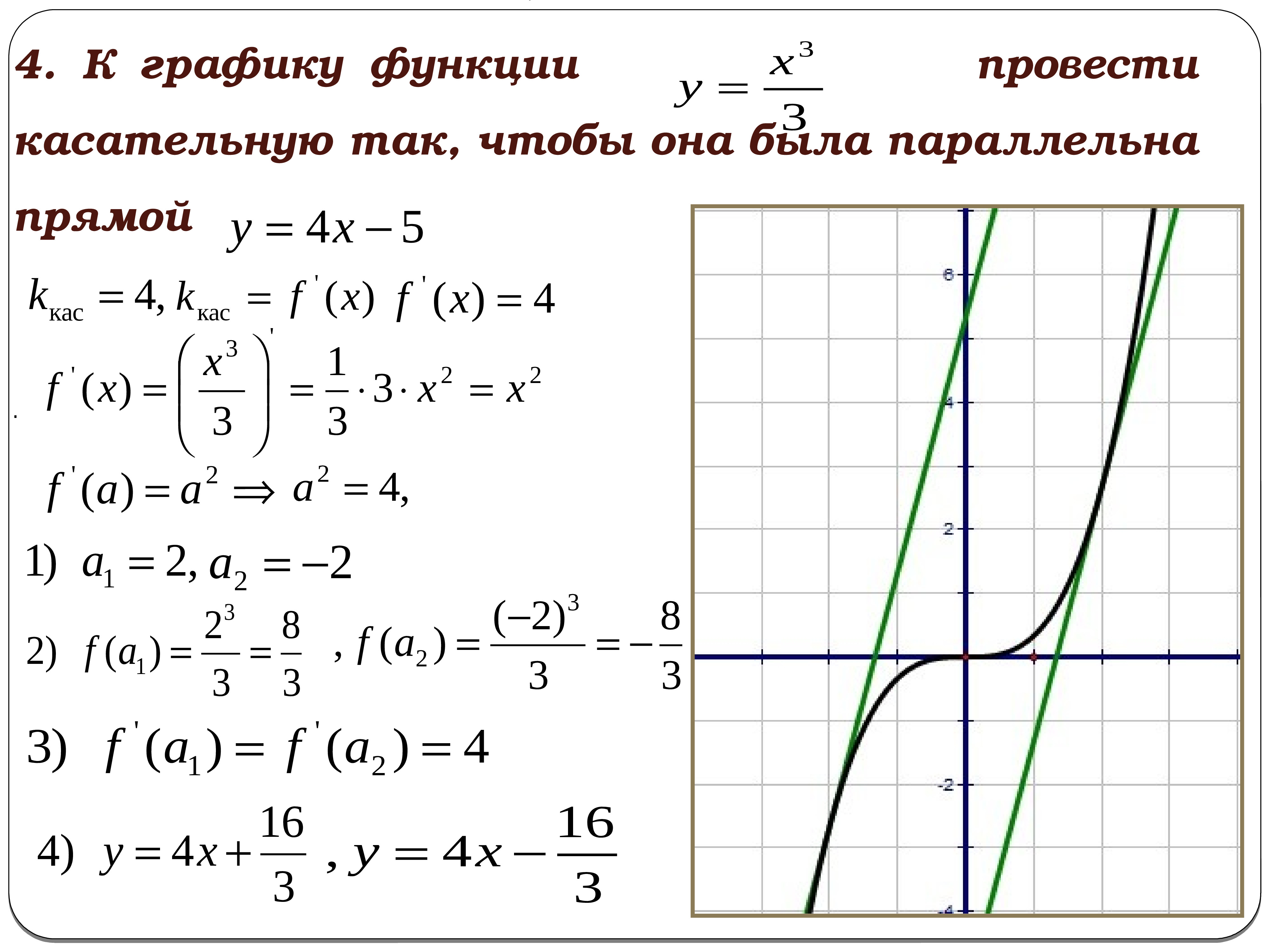
Практикуйтесь на различных функциях, чтобы улучшить свои навыки нахождения уравнений касательных.