Основы работы со степенями с рациональными показателями
Определение степени с рациональным показателем является важным элементом алгебры и математики в целом. Этот процесс включает в себя использование дробных чисел в показателе степени, что позволяет решать сложные задачи и уравнения более эффективно. В этой статье мы рассмотрим основные принципы и методы работы со степенями с рациональными показателями, а также предложим полезные советы для более глубокого понимания этой темы.


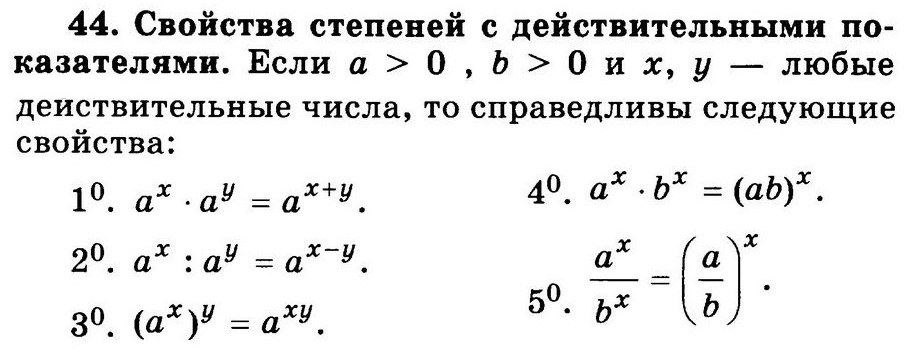
Запомните, что степень с рациональным показателем можно представить как корень: a^(m/n) = (n√a)^m.
Степень с рациональным и действительным показателем. Теория. Видеоурок 4. Алгебра 10 класс

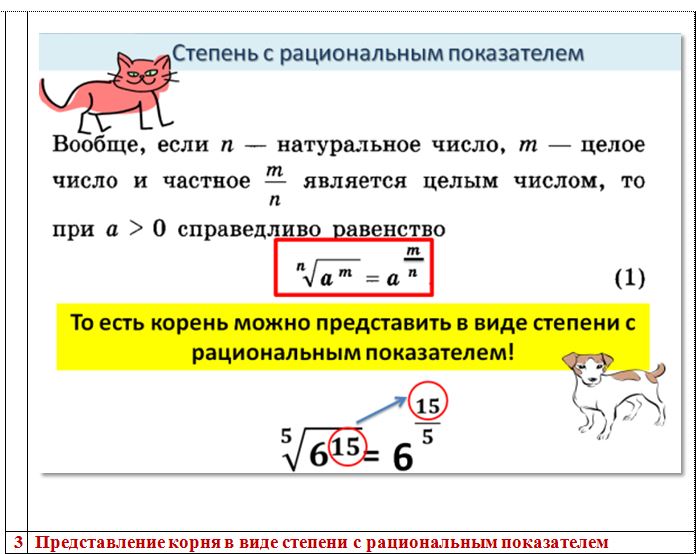
Практикуйте преобразование степеней с рациональными показателями в корни для лучшего понимания.
Степень числа с рациональным показателем. 11 класс.
Используйте свойства степеней, такие как a^(m/n) * a^(p/q) = a^((mq+np)/nq), чтобы упрощать выражения.
ПОНЯТИЕ СТЕПЕНИ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ

Помните, что отрицательный показатель степени означает обратное значение: a^(-m/n) = 1/(a^(m/n)).
Коротко и ясно по теме \

Изучите примеры применения степеней с рациональными показателями в реальных задачах, чтобы увидеть их практическую ценность.
11 класс, 8 урок, Понятие степени с любым рациональным показателем


Регулярно решайте задачи с использованием степеней с рациональными показателями для закрепления навыков.


Используйте графики для визуализации функций со степенями с рациональными показателями, чтобы лучше понять их поведение.
Изучите свойства логарифмов, так как они часто связаны с работой со степенями.

Запомните основные свойства степеней, такие как (a^m)^n = a^(mn), и применяйте их на практике.

Внимательно проверяйте свои вычисления, чтобы избежать ошибок при работе со сложными выражениями.