Как работать с опровержимой формулой в алгебре высказываний: полезные рекомендации
Опровержимая формула в алгебре высказываний представляет собой важный инструмент для логического анализа и построения доказательств. В этой статье мы собрали фотографии и полезные советы, которые помогут вам лучше понять и применять эту концепцию.



Начните с изучения базовых понятий алгебры высказываний, таких как конъюнкция, дизъюнкция и импликация.
Логика - Упрощение логических выражений. Законы алгебры логики


Используйте визуальные схемы и диаграммы для наглядного представления логических операций и их результатов.
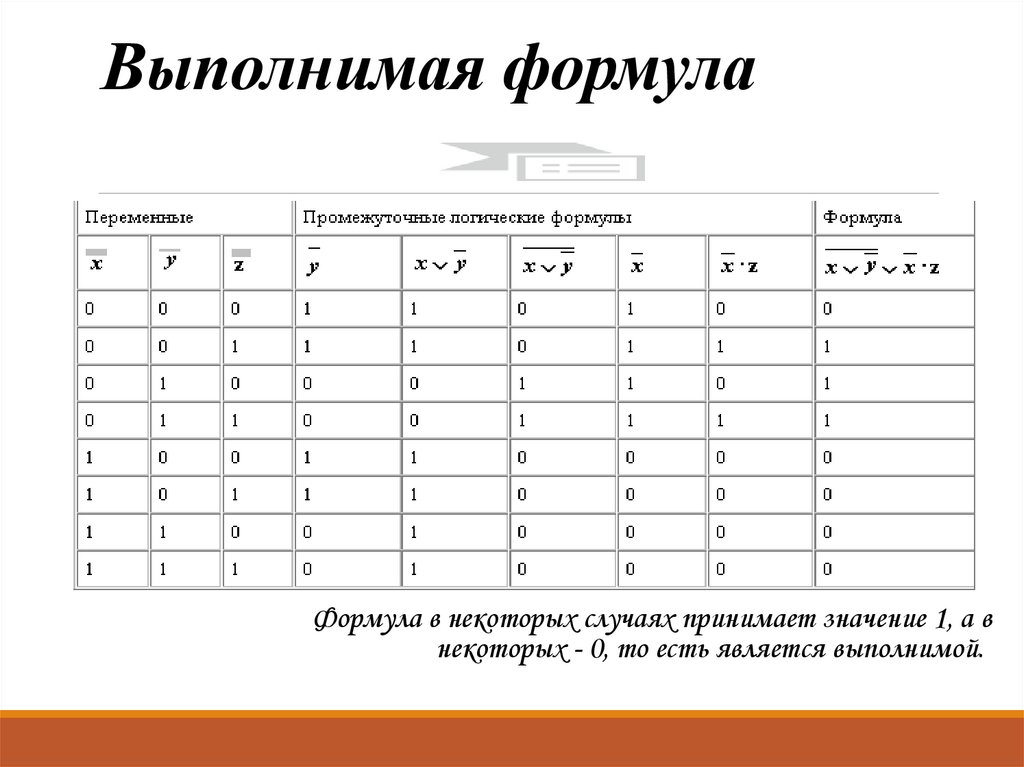
Формулы алгебры высказываний
Практикуйтесь в решении простых задач по алгебре высказываний, чтобы закрепить понимание теории.
Алгебра логики: Законы алгебры логики. Центр онлайн-обучения «Фоксфорд»


Обратите внимание на законы де Моргана, которые часто используются в преобразовании логических выражений.


При изучении опровержимых формул обращайте внимание на контрпримеры, которые могут подтвердить или опровергнуть гипотезу.


Используйте специализированные программы и онлайн-ресурсы для проверки своих решений и поиска ошибок.

Старайтесь разбивать сложные логические выражения на более простые компоненты для облегчения анализа.

Работайте в группе или обсуждайте задачи с коллегами, чтобы получать обратную связь и новые идеи.
#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0
Регулярно проверяйте и обновляйте свои знания, чтобы быть в курсе новейших методов и техник в алгебре высказываний.

Не бойтесь задавать вопросы и искать дополнительную информацию в учебниках и научных статьях по теме.