Построение гиперболы по уравнению: практические советы
В этом разделе мы рассмотрим процесс построения гиперболы по её уравнению, предоставим полезные советы и примеры, которые помогут вам лучше понять и применить этот математический метод.


Начните с определения общего уравнения гиперболы и его параметров.

Определите центр гиперболы, который находится на пересечении осей симметрии.
Гипербола. Функция k/x и её график
Найдите длину полуосей гиперболы, используя параметры уравнения.
Построение гиперболы

Определите фокусы гиперболы, используя формулу для расчета их координат.
функция y=k/x и ее график (гипербола) - 8 класс алгебра
Нарисуйте оси симметрии и отметьте центр гиперболы на графике.
§23 Построение гиперболы
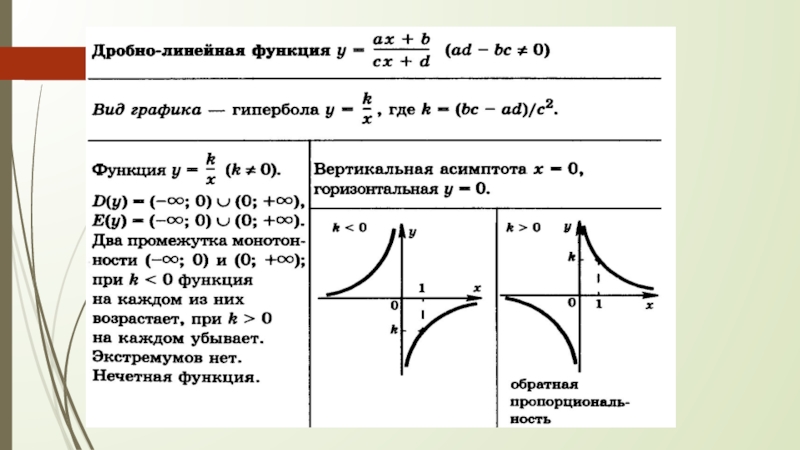
Отложите от центра расстояния, равные длинам полуосей, вдоль осей симметрии.
Проведите асимптоты гиперболы, используя уравнение её асимптот.
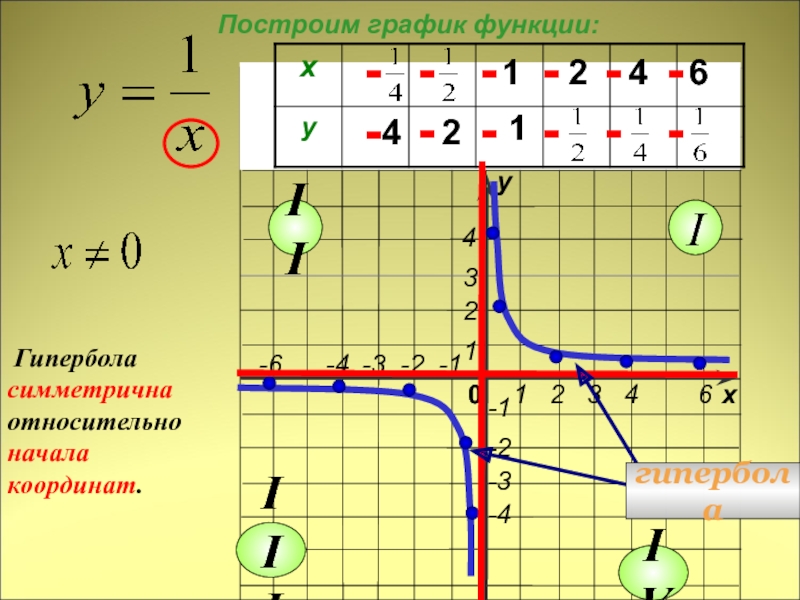
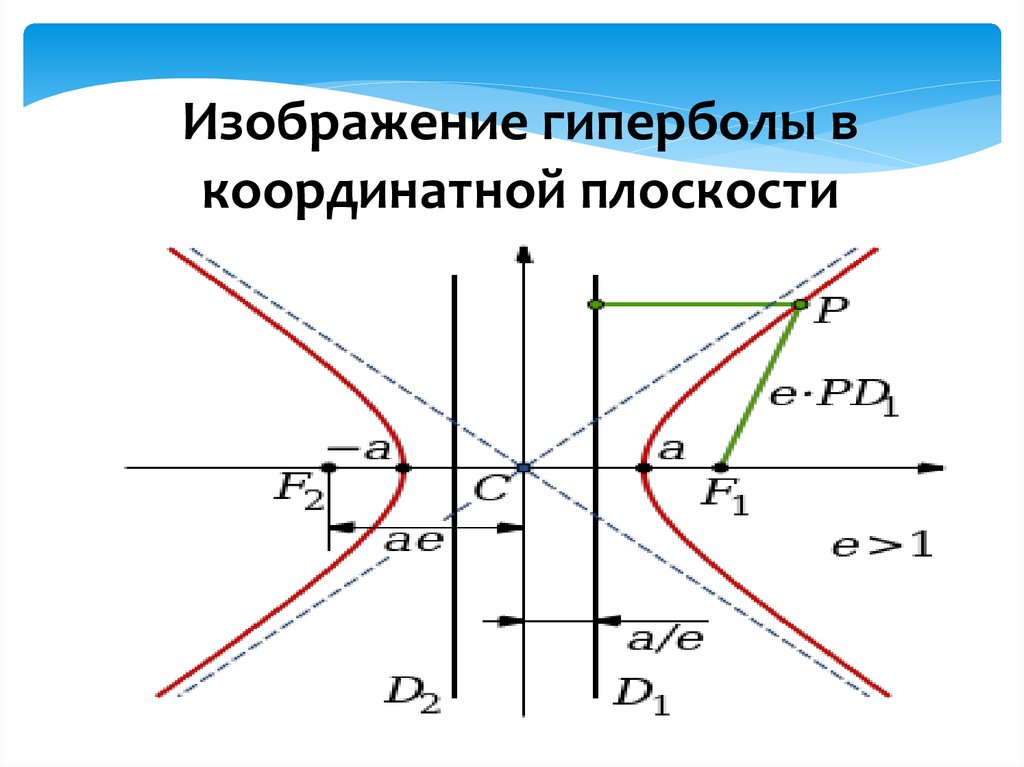
Нарисуйте гиперболу, используя полученные данные и учитывая её симметрию относительно осей.
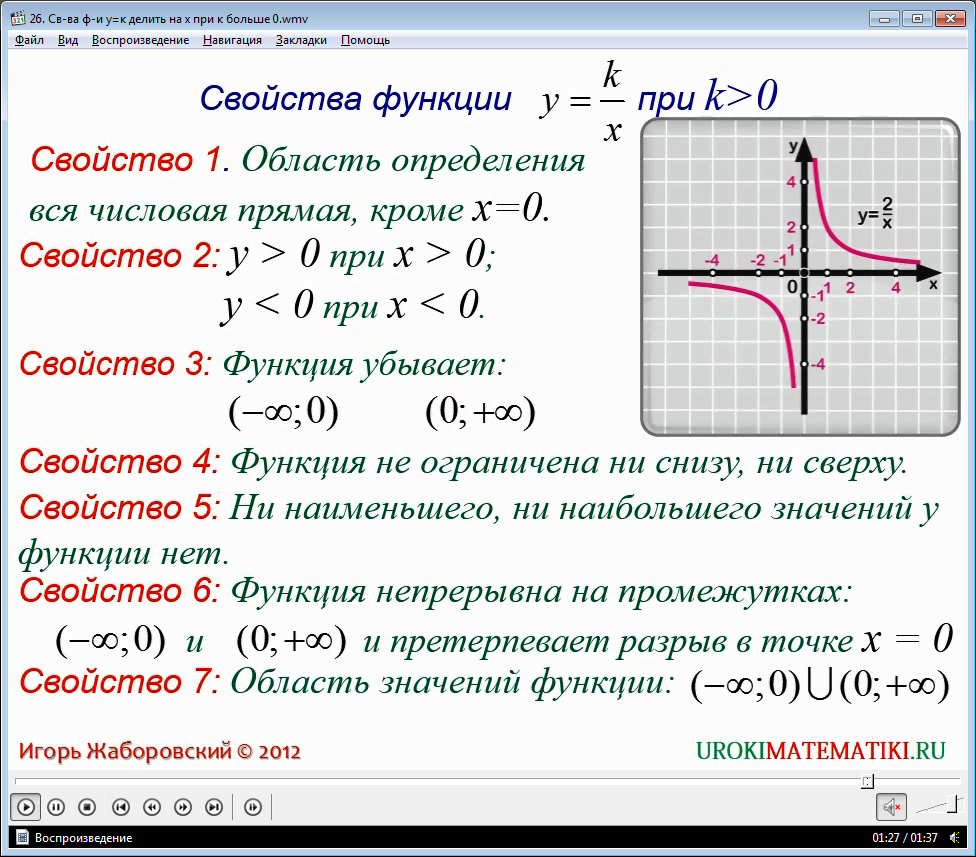
Проверьте правильность построения, сравнивая с уравнением гиперболы.

Используйте графические программы или онлайн-калькуляторы для проверки и визуализации гиперболы.