Всё о площади треугольника: как рассчитать и использовать формулы

На этой странице вы найдете полезные советы и методы расчета площади треугольника, включая популярные формулы и примеры их применения. Узнайте, как правильно применять различные методы для получения точных результатов.

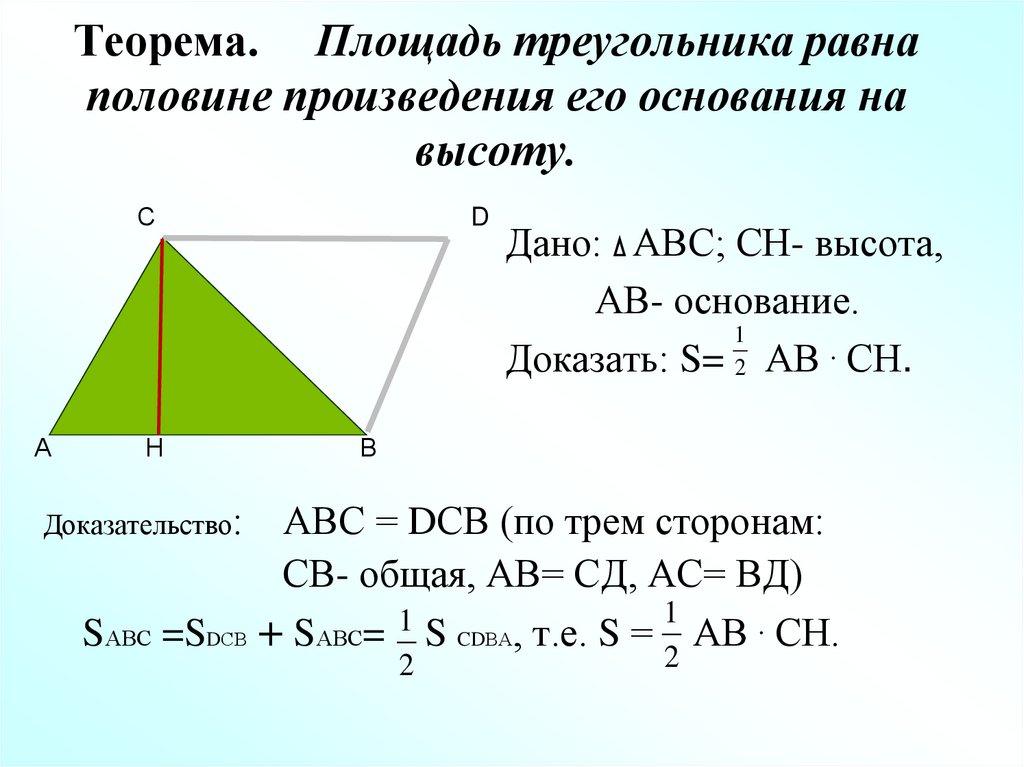
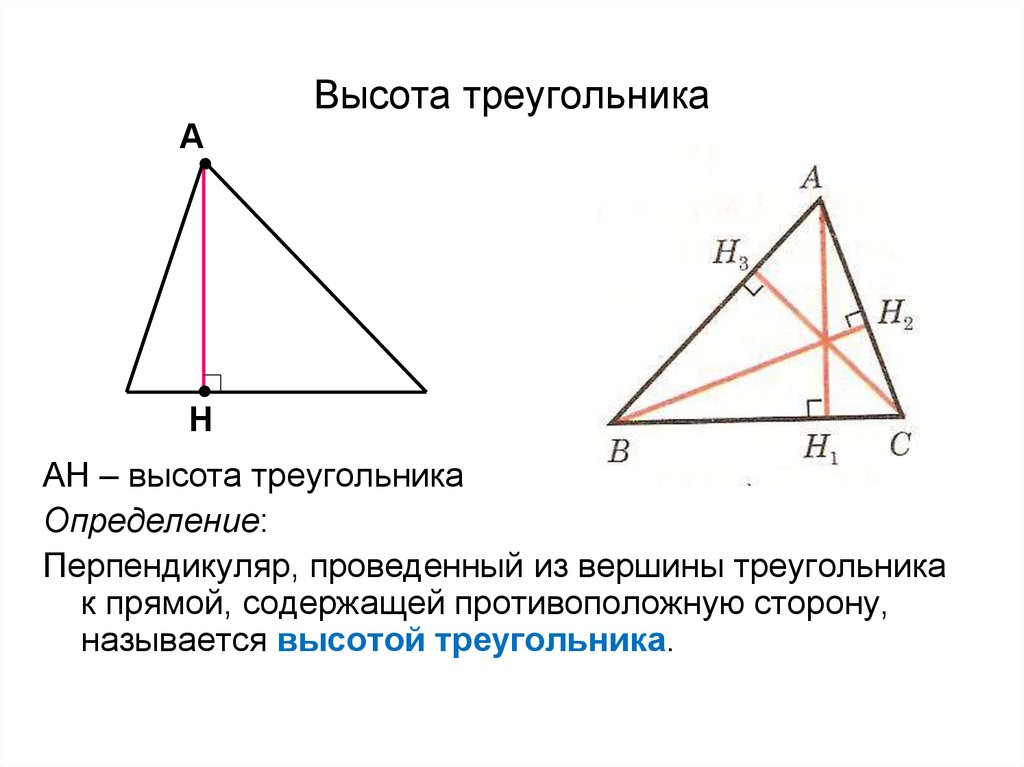
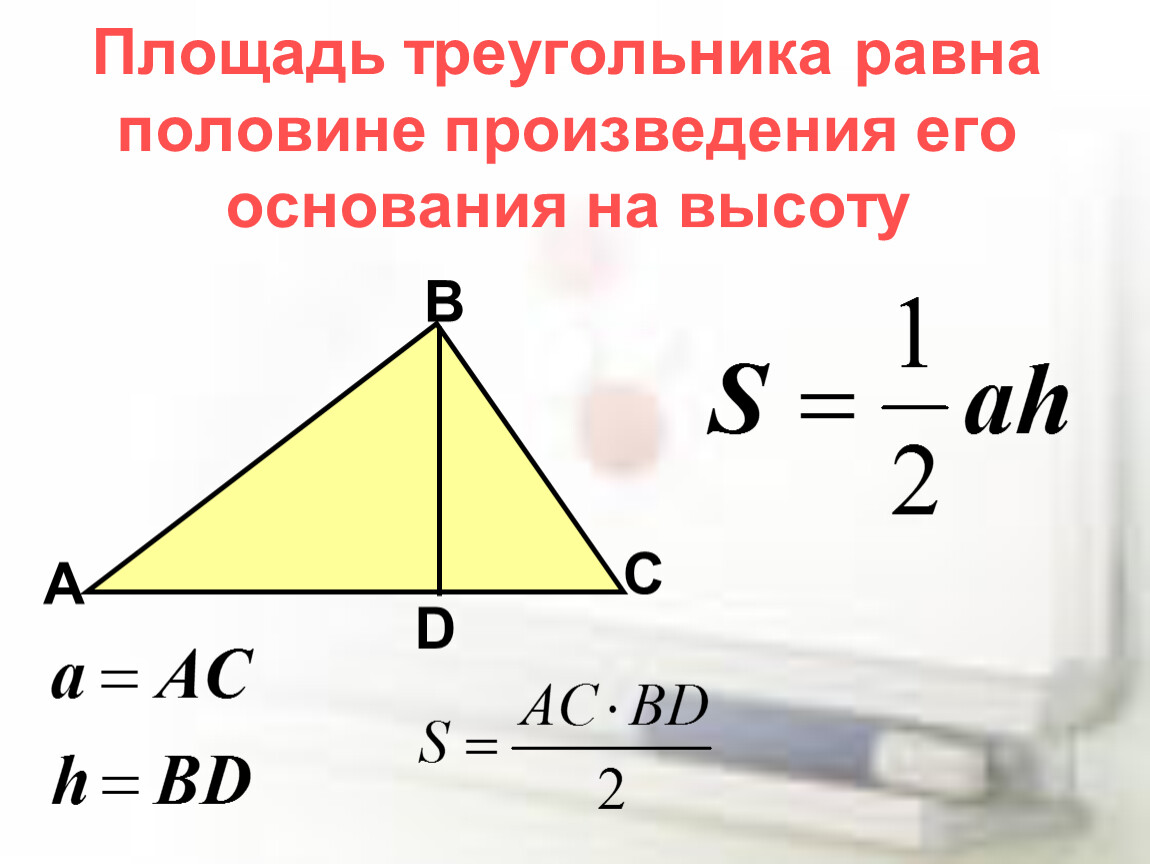
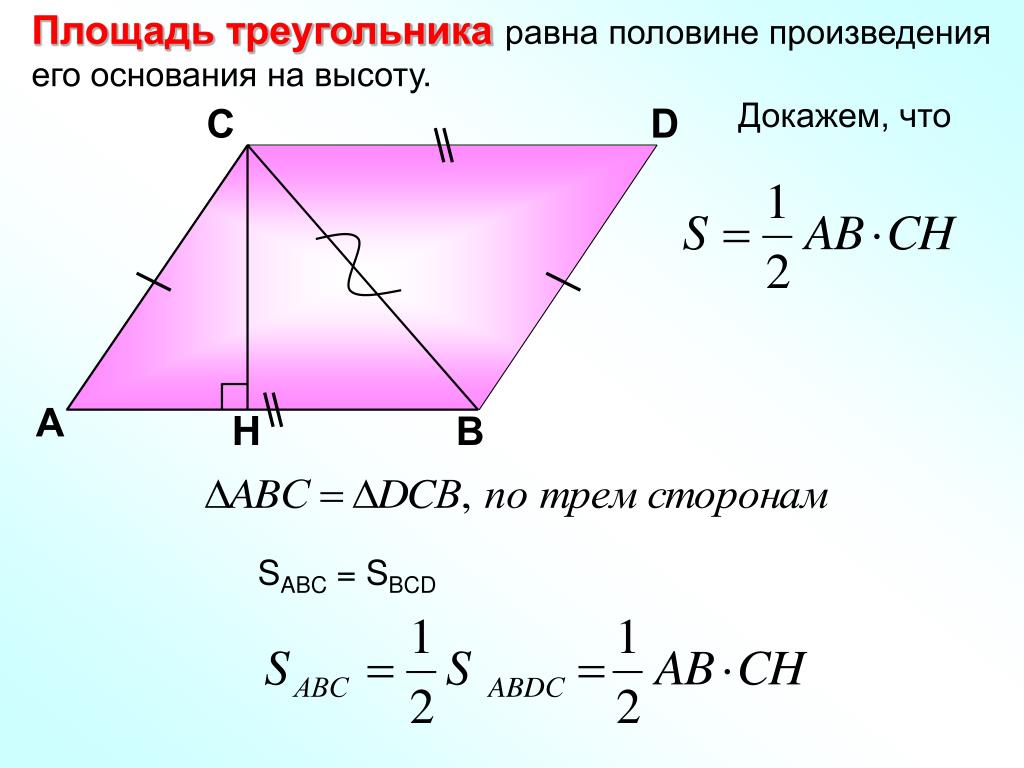
Используйте формулу площади треугольника через основание и высоту: Площадь = (основание × высота) / 2.

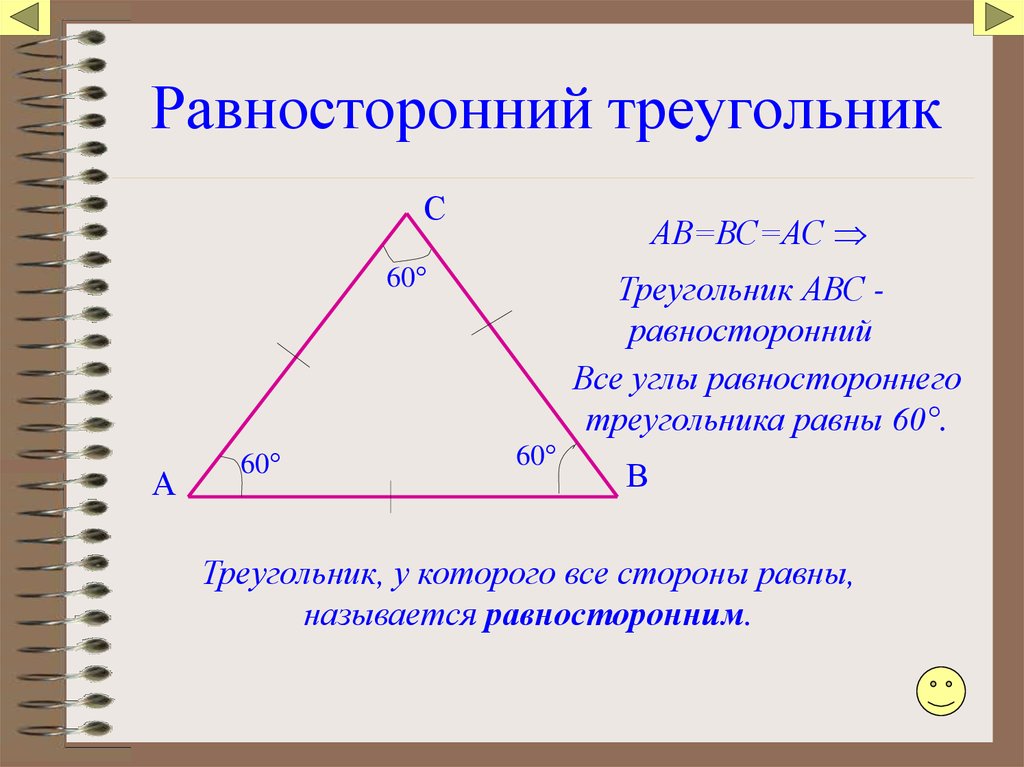
Для треугольника с известными сторонами применяйте формулу Герона: Площадь = √[s(s-a)(s-b)(s-c)], где s = (a+b+c)/2.

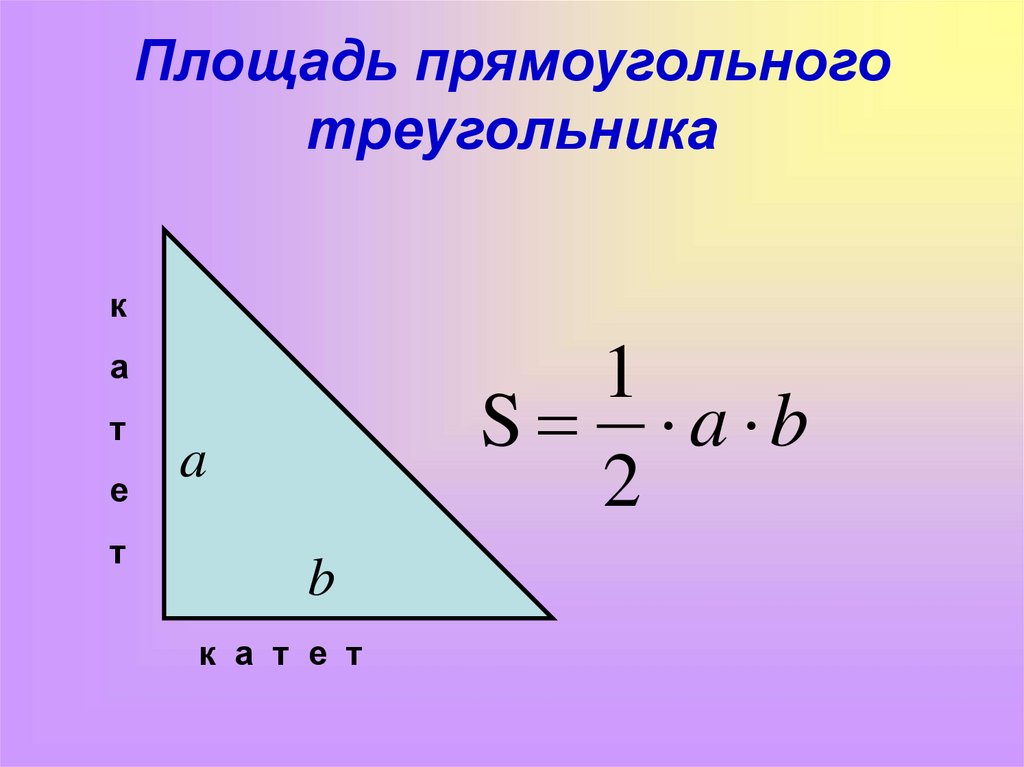
Если известны два угла и сторона между ними, применяйте формулу: Площадь = (a^2 × sin(B) × sin(C)) / (2 × sin(A)).

При наличии координат вершин треугольника используйте формулу: Площадь = 0.5 × |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)|.

Для равнобедренного треугольника с известной высотой и основанием: Площадь = (основание × высота) / 2, а высоту можно найти из формулы h = √(a^2 - (b/2)^2).

Площадь треугольника можно также найти, используя полярные координаты, если известны радиусы и углы: Площадь = 0.5 × r1 × r2 × sin(θ).

Когда требуется площадь треугольника в треугольной сетке, измеряйте клетки и суммируйте их для вычисления общей площади.

Для треугольников с известными углами и одной стороной используйте формулу: Площадь = 0.5 × a^2 × sin(B) × sin(C) / sin(A).

При расчетах площади треугольника в 3D-пространстве используйте векторные методы: Площадь = 0.5 × |AB × AC|, где AB и AC - векторные координаты.

Для проверки результатов используйте несколько различных методов и сравните их, чтобы удостовериться в точности расчетов.