Понимание высоты к основанию в равнобедренном треугольнике: полезные рекомендации и изображения

На этой странице вы найдете подборку фотографий и полезных советов, связанных с высотой, проведенной к основанию равнобедренного треугольника. Узнайте, как правильно измерить высоту и применить эти знания для решения задач.

При работе с равнобедренным треугольником, всегда проверяйте, что высота проведена именно к основанию, а не к боковой стороне.

Используйте формулу для вычисления высоты: h=a2−(b2)2h = /sqrt{a^2 - /left(/frac{b}{2}/right)^2}h=a2−(2b​)2​, где aaa - длина боковой стороны, а bbb - длина основания.

Помните, что высота в равнобедренном треугольнике делит основание пополам, поэтому можно использовать это свойство для упрощения расчетов.

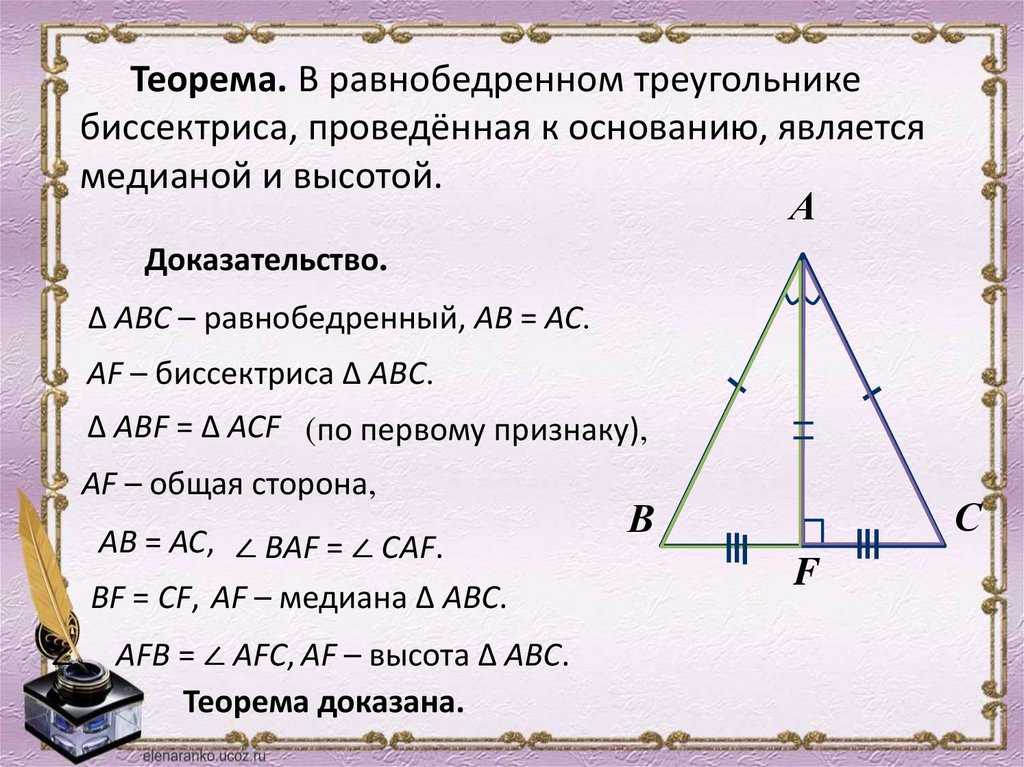
При рисовании треугольника на бумаге, аккуратно чертите высоту, чтобы избежать ошибок в расчетах.

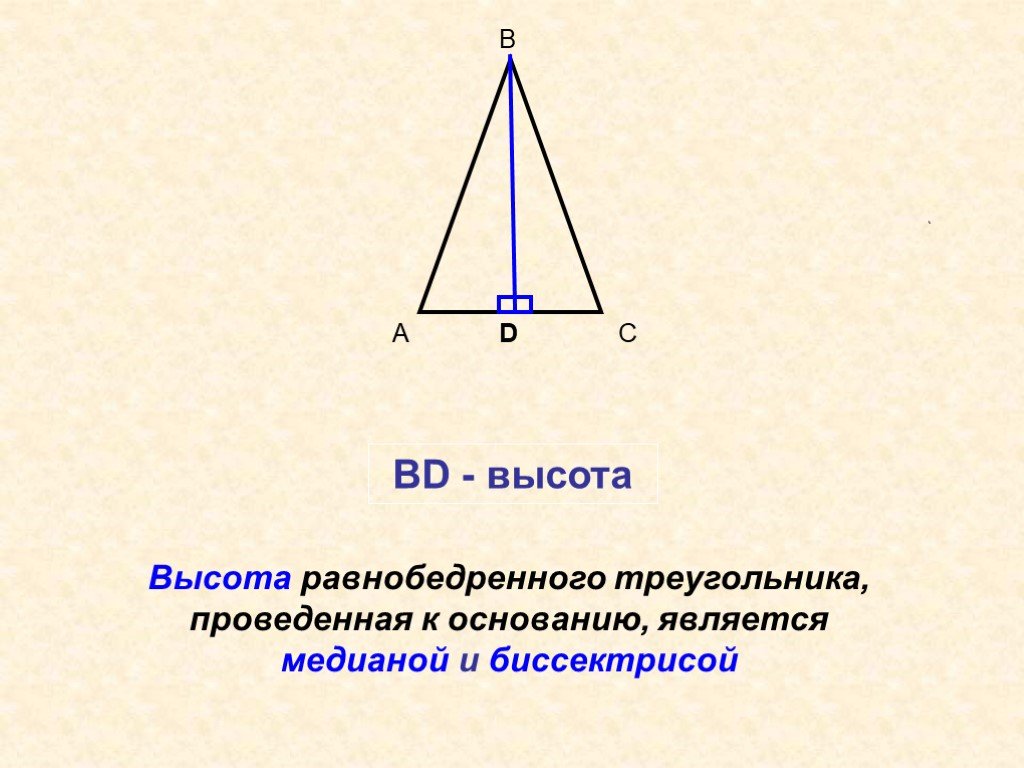
Если вам нужно найти высоту треугольника по его площади, используйте формулу h=2⋅Sbh = /frac{2 /cdot S}{b}h=b2⋅S​, где SSS - площадь треугольника, а bbb - основание.

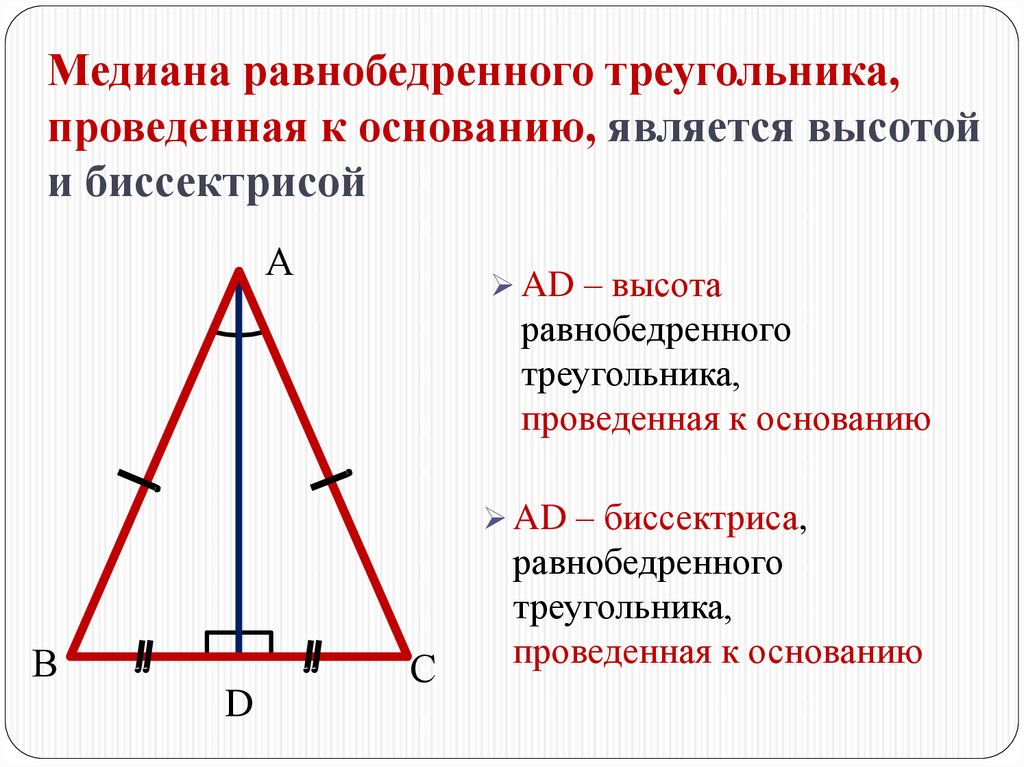
Знание свойств равнобедренного треугольника, таких как симметрия и равенство углов, поможет вам лучше понимать и использовать высоту к основанию.

Для точных измерений используйте инструменты, такие как линейка и транспортир, чтобы избежать погрешностей.

Практикуйтесь в решении задач с разными размерами и пропорциями треугольников для улучшения навыков работы с высотой.

Запомните, что высота равнобедренного треугольника всегда будет перпендикулярна основанию.

Рассмотрите использование графического программного обеспечения для визуализации треугольников и высот, что может облегчить понимание и вычисления.