Определение параметров треугольника по двум сторонам и углу
Решение треугольника по двум сторонам и углу между ними - важная задача в геометрии. Зная две стороны и угол между ними, можно легко вычислить третью сторону и другие углы, используя теорему косинусов и другие геометрические методы. Этот процесс может быть полезен в различных областях, таких как строительство, инженерия и навигация.
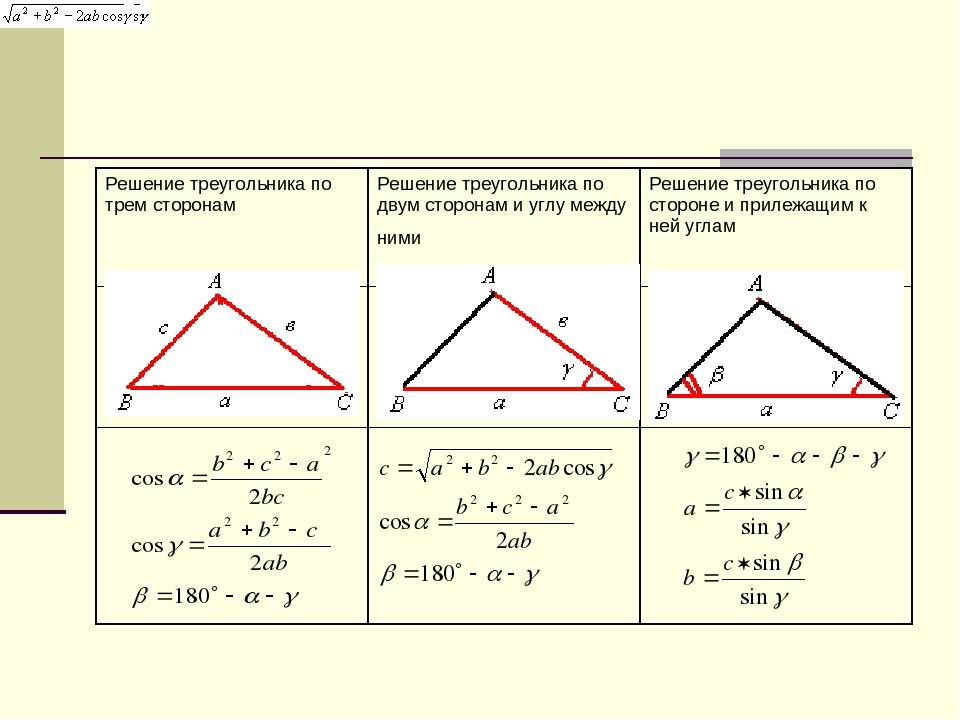
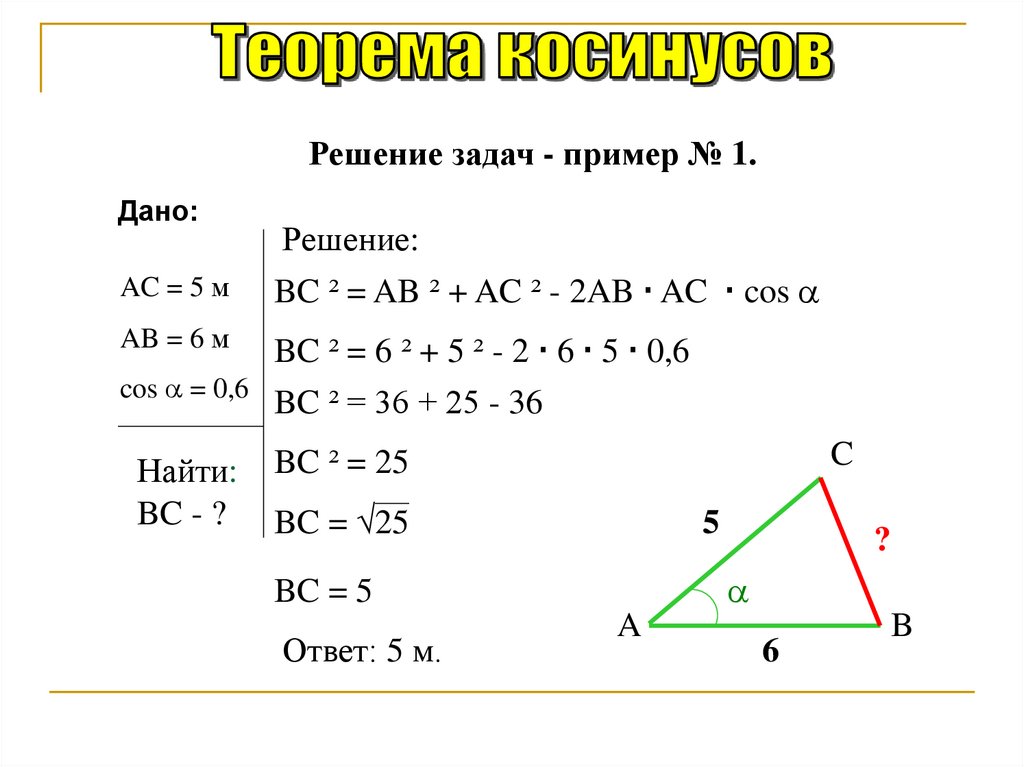
Используйте теорему косинусов для вычисления третьей стороны треугольника.
Запомните формулу: c2=a2+b2−2ab⋅cos(γ)c^2 = a^2 + b^2 - 2ab /cdot /cos(/gamma)c2=a2+b2−2ab⋅cos(γ), где aaa и bbb - известные стороны, а γ/gammaγ - угол между ними.
7 класс построение треугольника по двум сторонам и углу между ними

Убедитесь, что ваш калькулятор настроен на правильный режим: градусы или радианы, в зависимости от задачи.


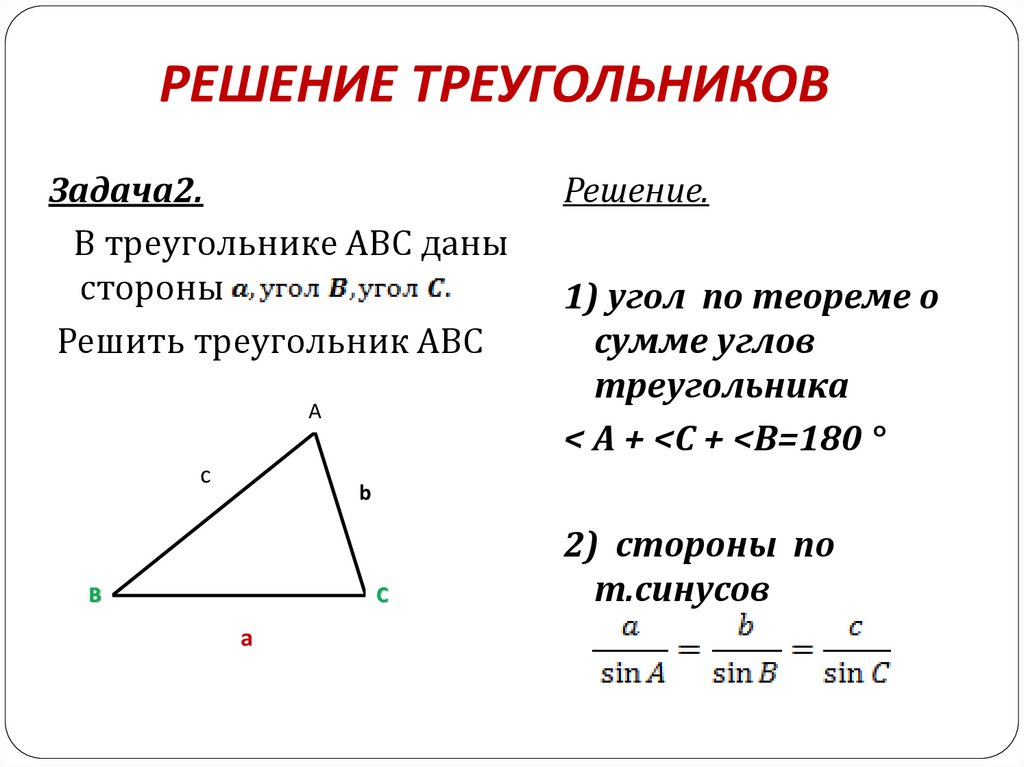
После нахождения третьей стороны используйте теорему синусов для вычисления остальных углов треугольника.
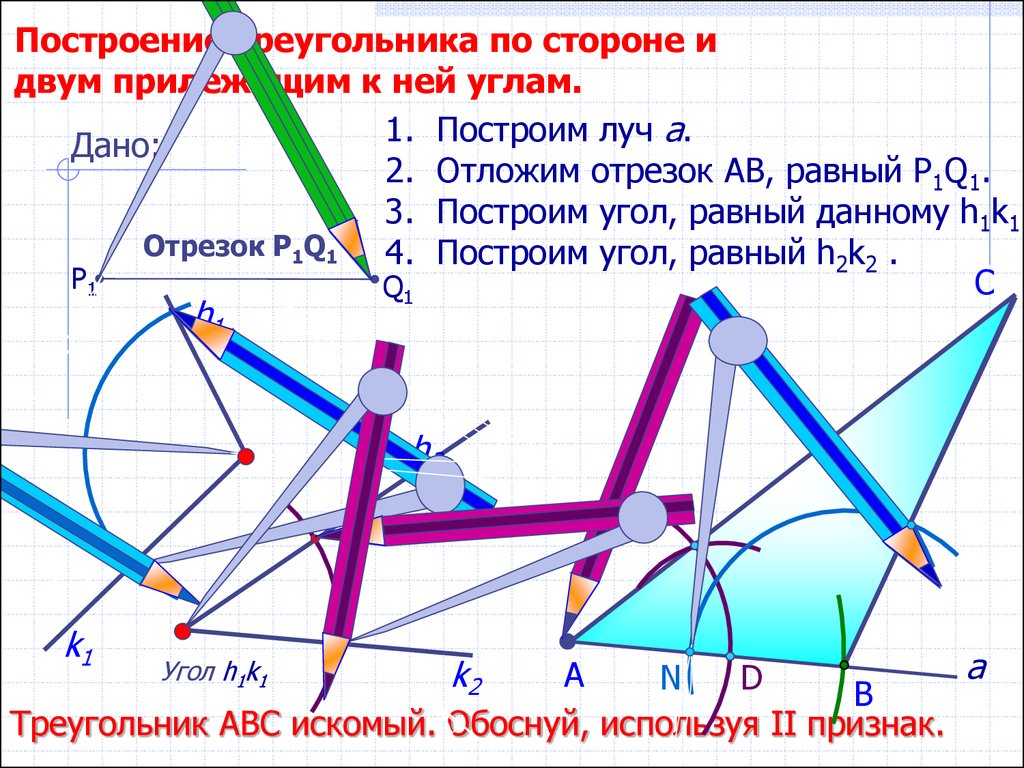
Построение треугольника по двум сторонам и углу между ними
Запомните формулу теоремы синусов: asin(α)=bsin(β)=csin(γ)/frac{a}{/sin(/alpha)} = /frac{b}{/sin(/beta)} = /frac{c}{/sin(/gamma)}sin(α)a=sin(β)b=sin(γ)c.

Проверьте правильность своих вычислений, пересчитав углы и стороны, чтобы убедиться, что их сумма соответствует 180 градусам.

Используйте геометрические чертежи для визуализации треугольника и проверки правильности решения.

Обратите внимание на возможные ошибки округления при вычислениях, особенно при работе с углами и тригонометрическими функциями.
Если вы используете программное обеспечение для расчетов, убедитесь в правильности вводимых данных и настроек программы.
Построить треугольник по двум сторонам и углу между ними.
Практикуйтесь в решении различных задач на треугольники, чтобы лучше запомнить формулы и методы решения.