Как использовать свойства медианы и высоты в прямоугольном треугольнике

На этой странице вы найдете полезные советы и подборку фотографий, иллюстрирующих свойства медианы и высоты в прямоугольном треугольнике. Эти геометрические элементы играют важную роль в решении множества задач и в практических приложениях.

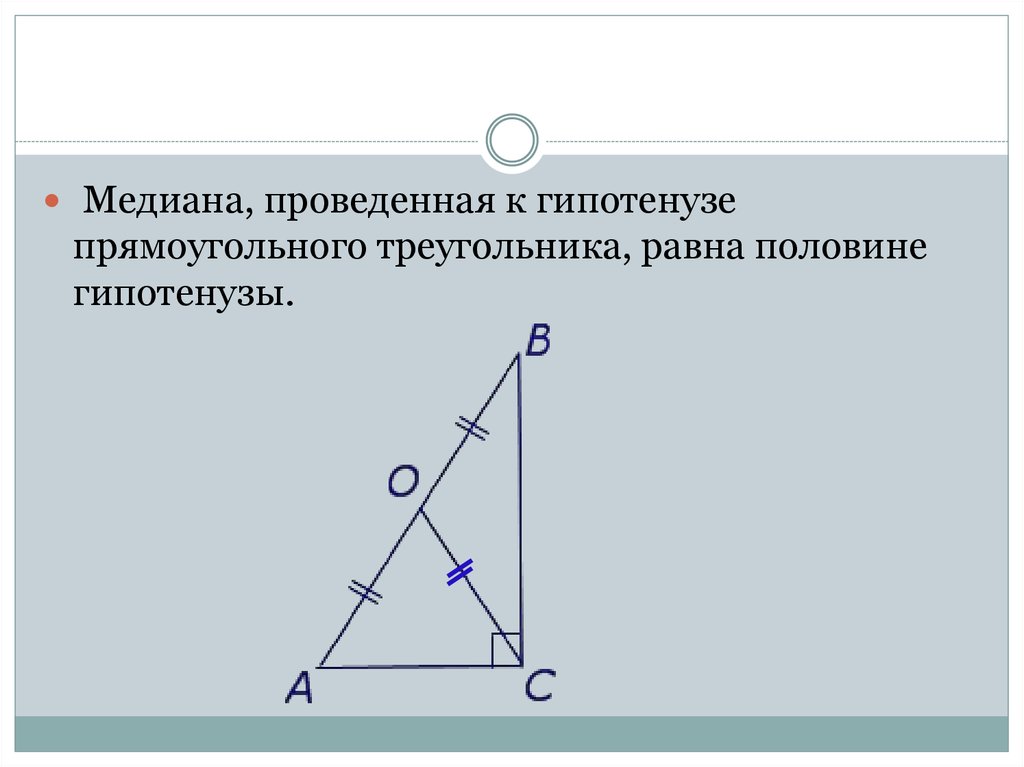
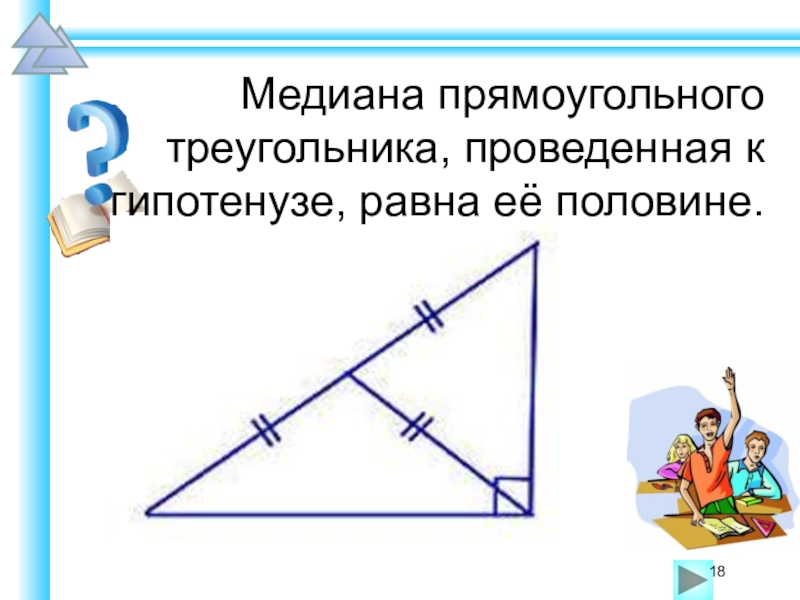
Помните, что медиана, проведенная из вершины прямого угла прямоугольного треугольника, делит гипотенузу на две равные части.

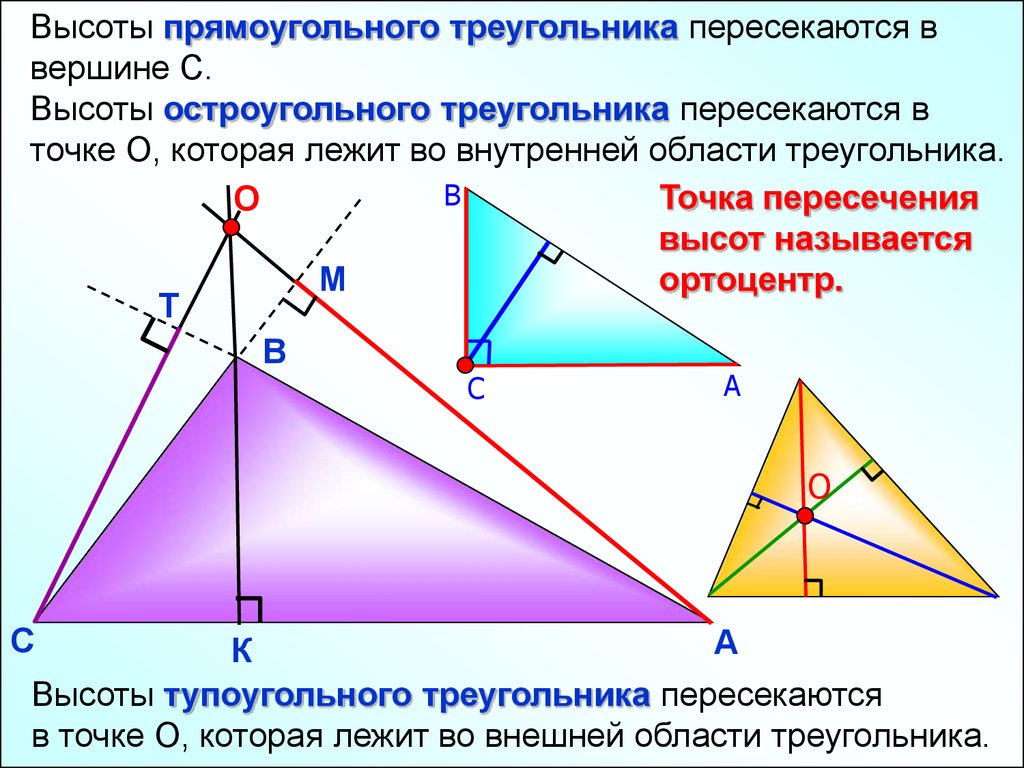
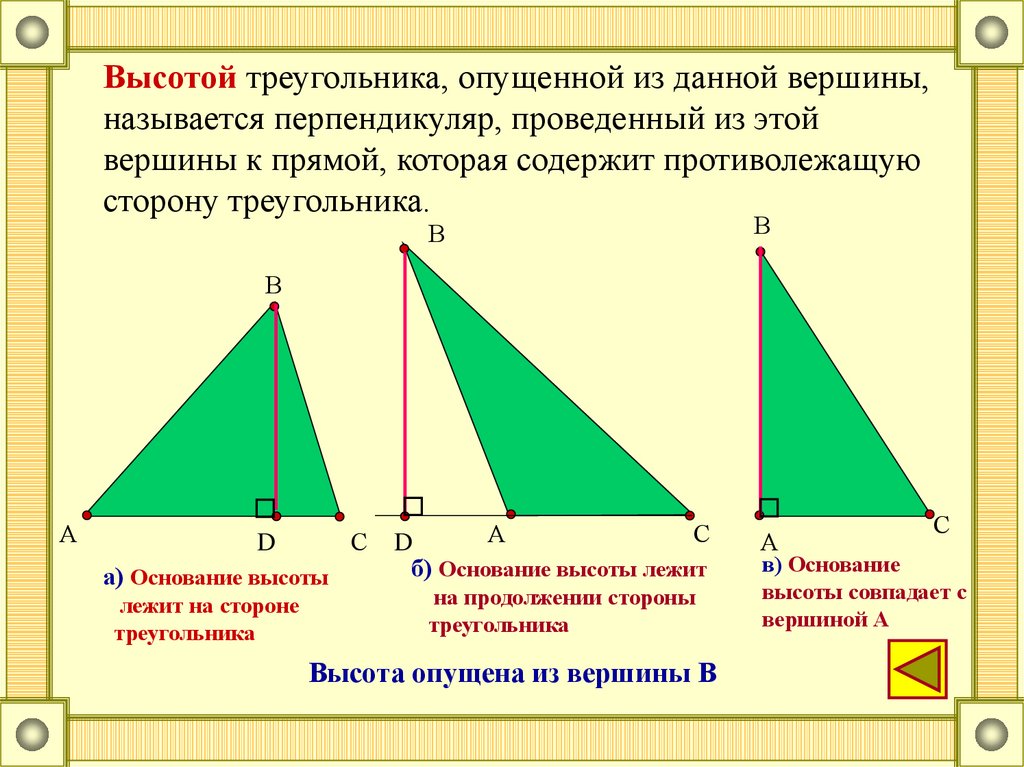
Высота, опущенная из вершины прямого угла на гипотенузу, является также медианой и биссектрисой.

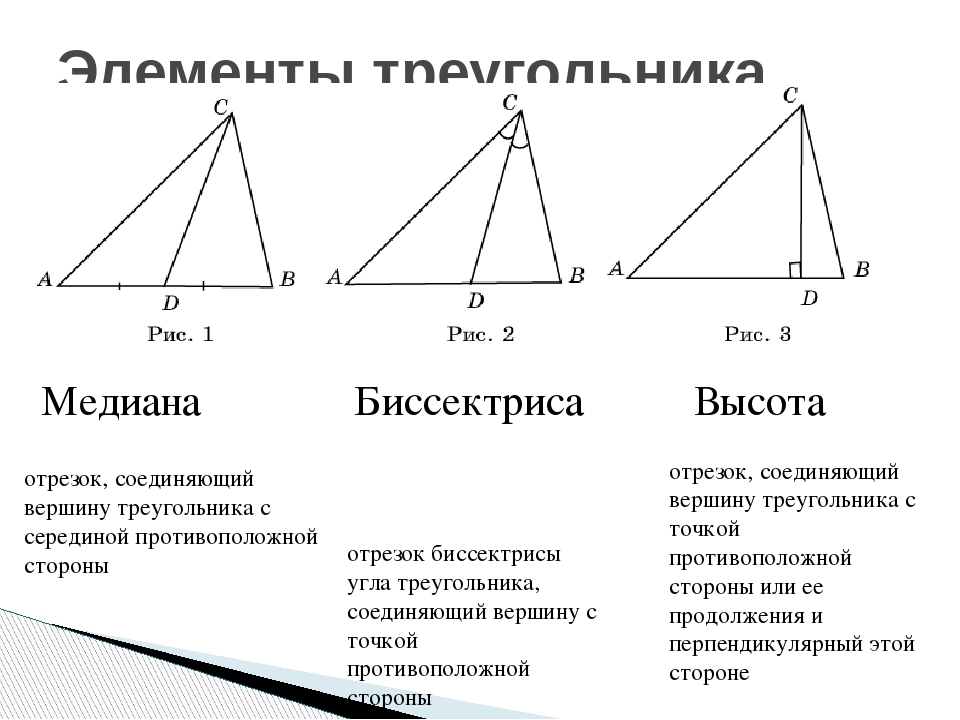
Используйте теорему Пифагора для нахождения длины медианы или высоты в прямоугольном треугольнике.

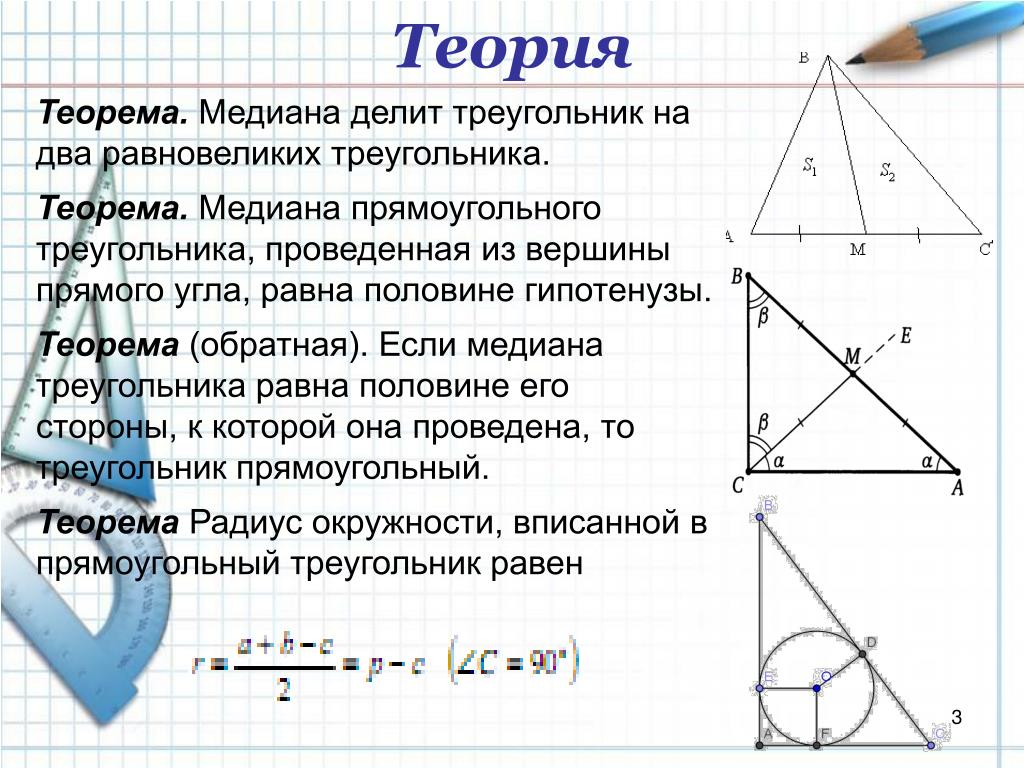
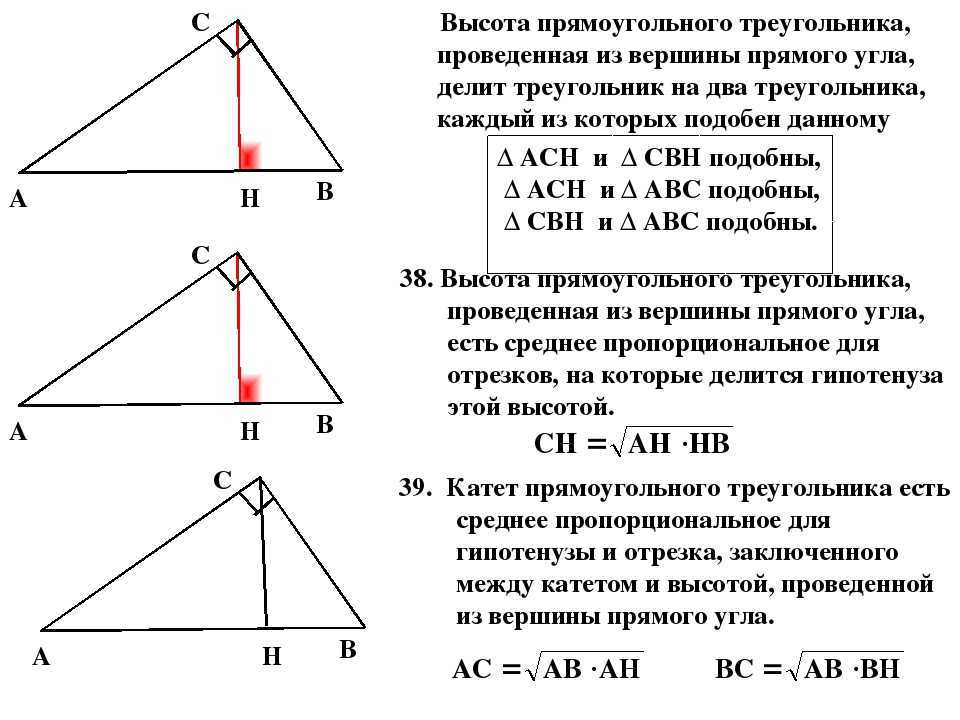
Запомните, что высота, опущенная из вершины прямого угла, делит прямоугольный треугольник на два подобных треугольника.

Для нахождения длины высоты можно использовать формулу: высота равна произведению катетов, деленному на гипотенузу.

Медиана в прямоугольном треугольнике может служить радиусом описанной окружности.

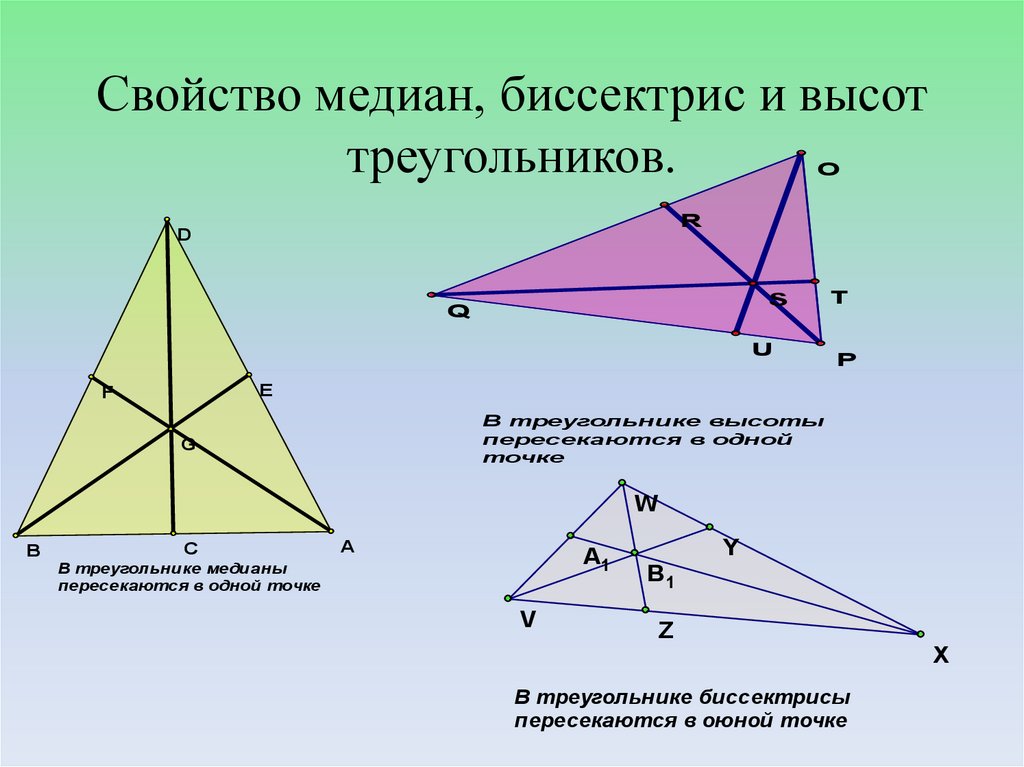
Используйте геометрические чертежи и схемы для лучшего понимания свойств медианы и высоты.

Практикуйтесь в решении задач на нахождение медианы и высоты для закрепления материала.

Обратите внимание, что медиана и высота имеют разные свойства в зависимости от типа треугольника.

Изучение свойств медианы и высоты поможет вам лучше понимать геометрию и применять эти знания на практике.