Основы теоремы о пересечении высот треугольника и её применение
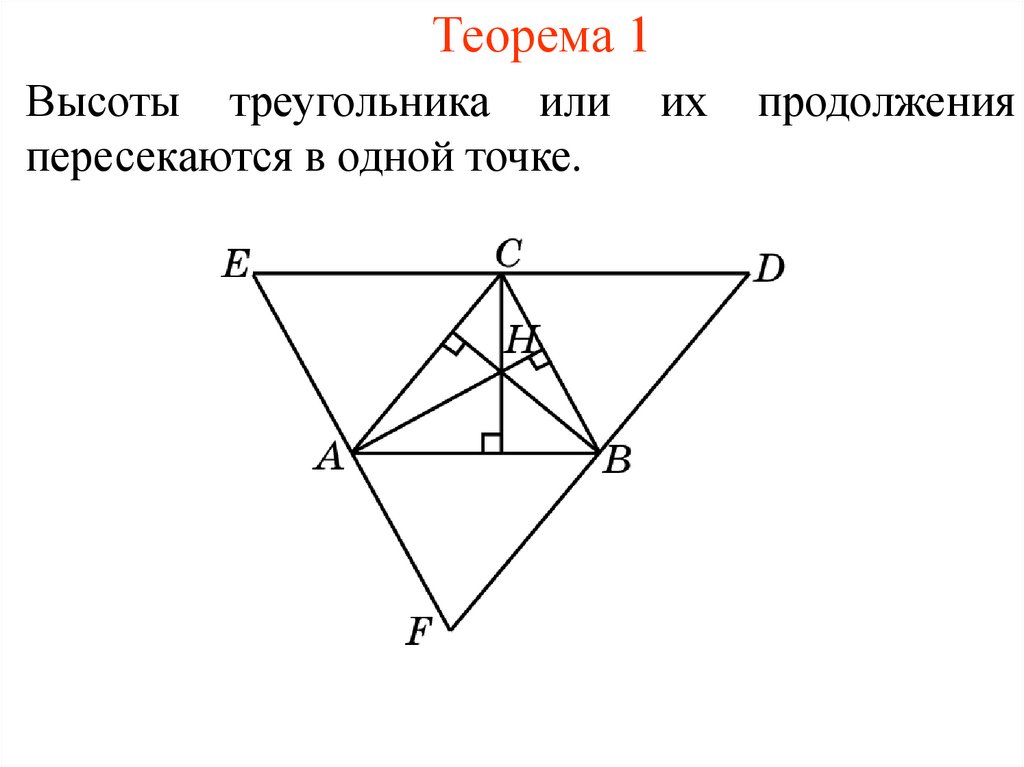
Теорема о пересечении высот треугольника утверждает, что высоты любого треугольника пересекаются в одной точке, называемой ортоцентром. Это важное свойство, которое имеет множество применений в геометрии и задачах на построение.
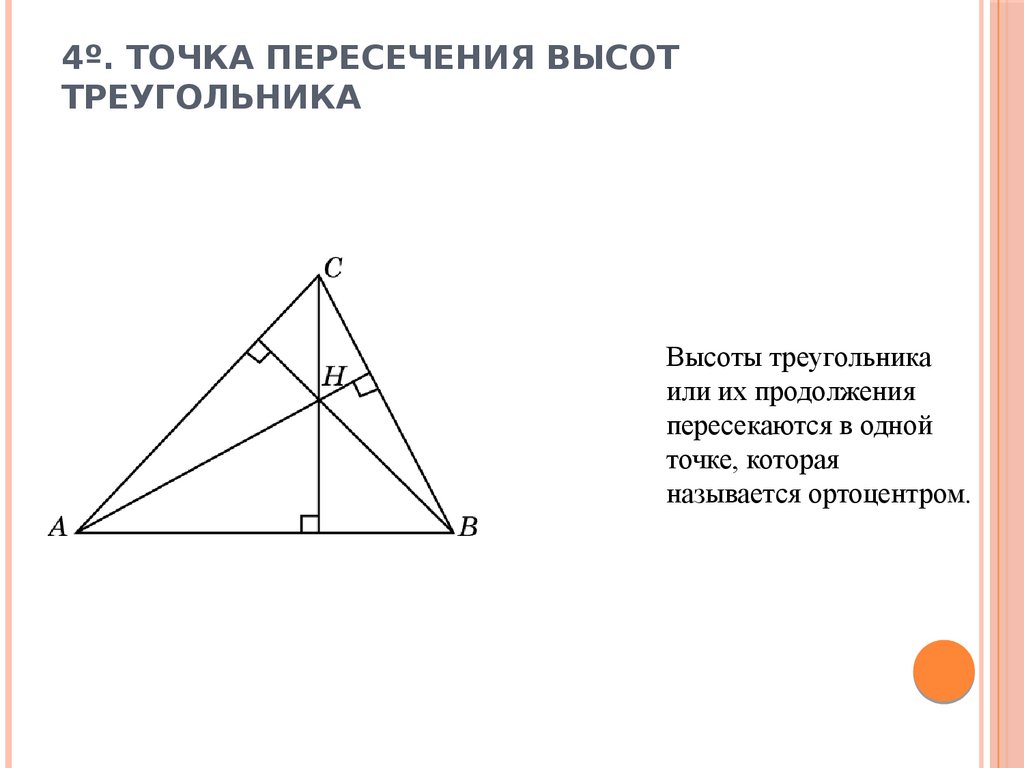
Изучите определение и свойства ортоцентра, чтобы лучше понимать теорему.

Попробуйте построить высоты треугольника и найти их точку пересечения самостоятельно.
Используйте программное обеспечение для геометрии, чтобы визуализировать и проверять свои построения.
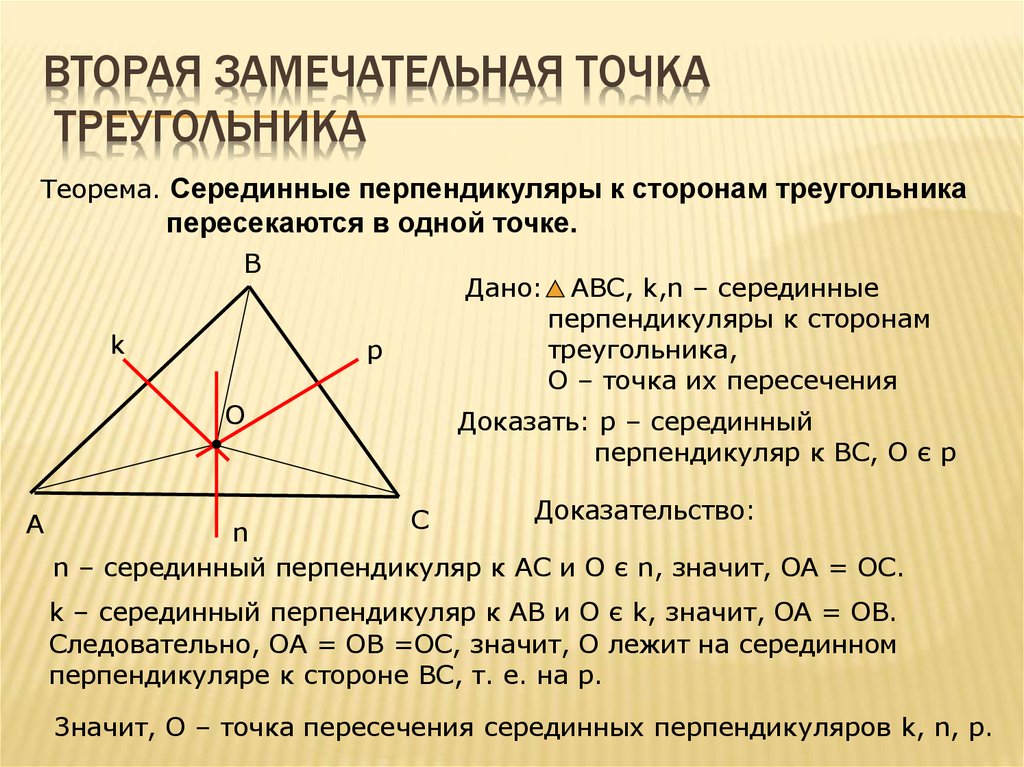
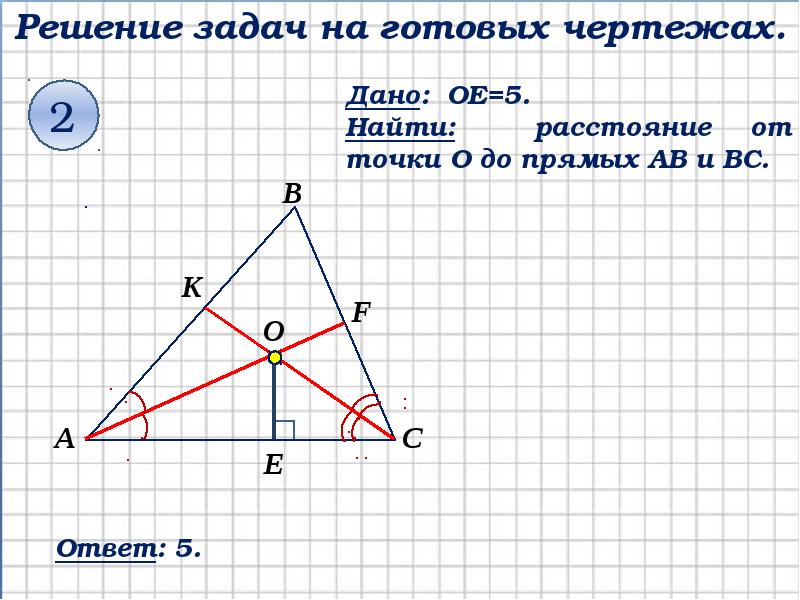
Теорема о пересечении высот треугольника

Понимание теоремы о пересечении высот поможет решать сложные задачи на экзаменах и олимпиадах.
72 Теорема о пересечении высот треугольника
Регулярно практикуйтесь в построении и нахождении ортоцентра для разных типов треугольников.
Изучите доказательства теоремы из разных источников для углубленного понимания.
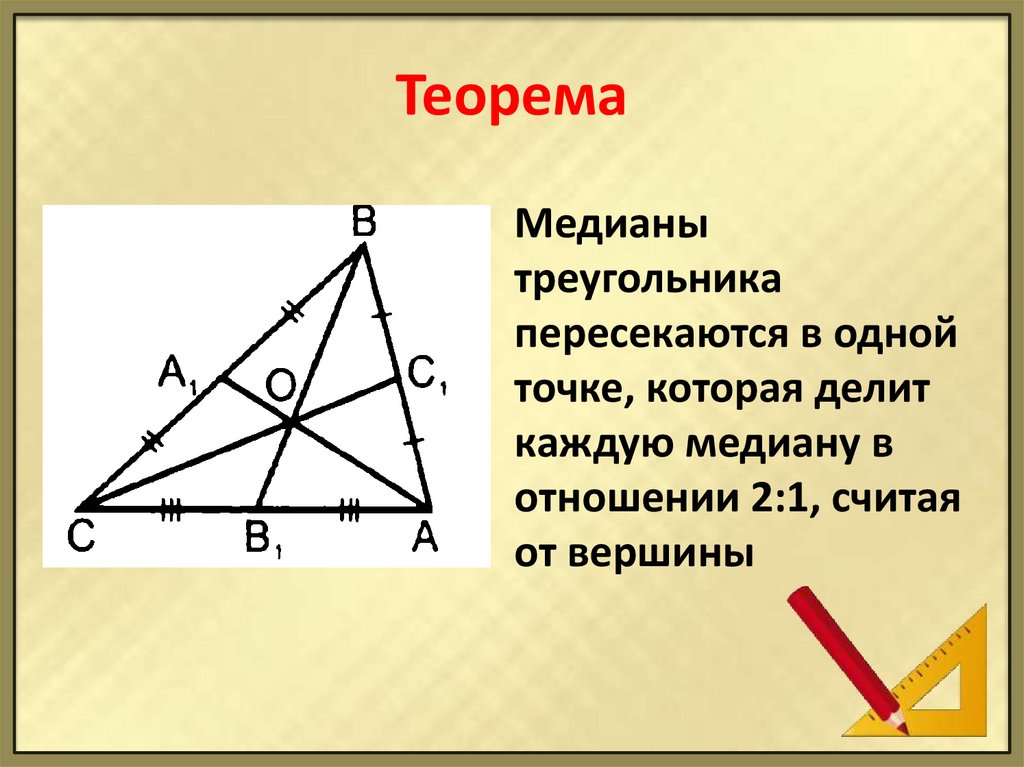
Обратите внимание на то, как высоты и ортоцентр взаимосвязаны с другими элементами треугольника, такими как медианы и биссектрисы.

Используйте теорему о пересечении высот для решения задач на нахождение углов и сторон треугольника.
«Фокус с картами» — теорема о неподвижной точке
Применяйте знания о теореме для решения задач на построение, где требуется найти точку пересечения высот.
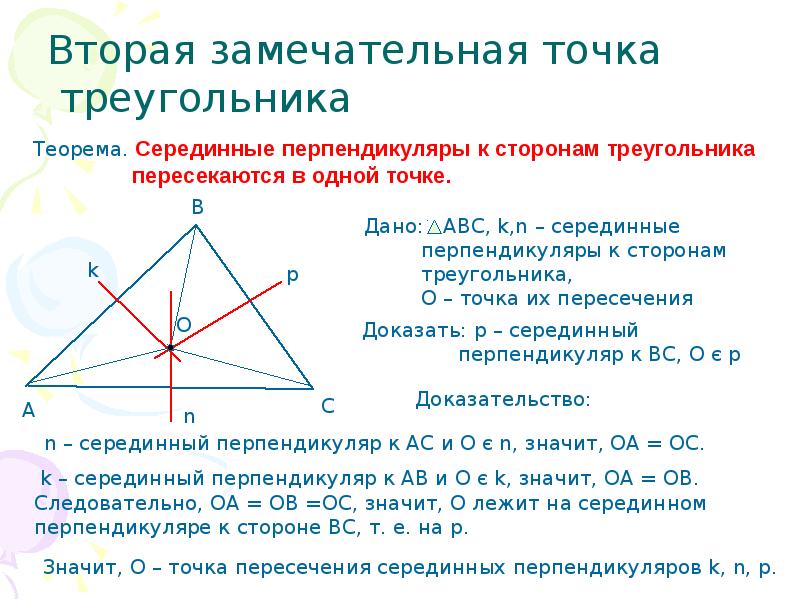
Обсуждайте свои построения и решения задач с учителями и одноклассниками для получения обратной связи и улучшения своих навыков.