Как периметры подобных треугольников связаны между собой
Теорема о соотношении периметров подобных треугольников является важной частью геометрии, помогающей понять пропорциональные отношения между сторонами подобных фигур. В этом материале вы найдете не только объяснение теоремы, но и полезные советы по ее применению.
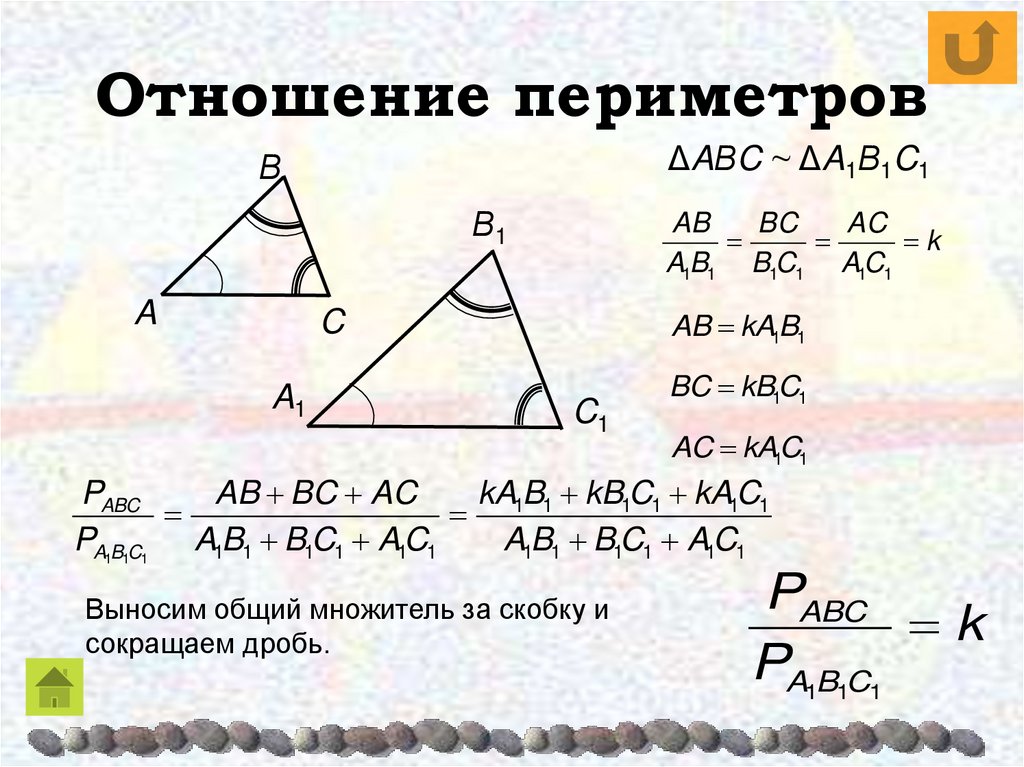
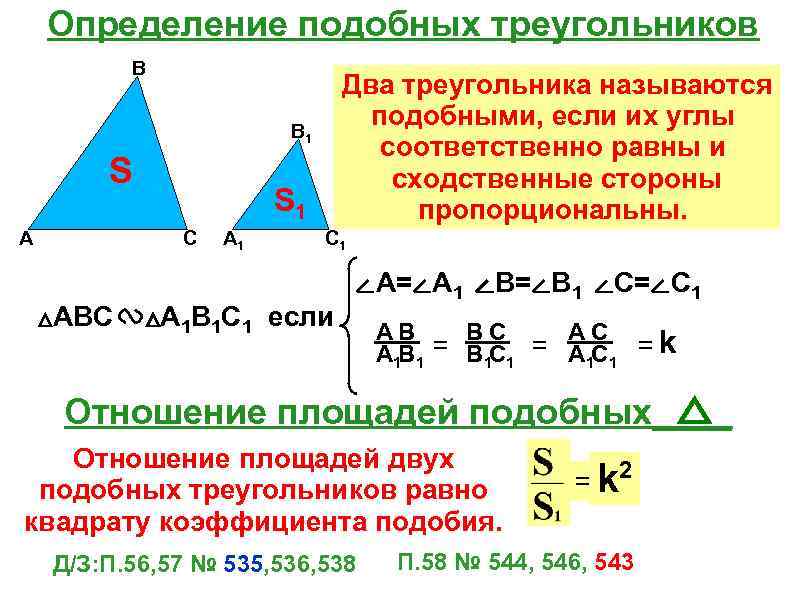
Изучите основные определения подобия треугольников, чтобы лучше понять суть теоремы.
Подобие треугольников. Признаки подобия треугольников (часть 1) - Математика
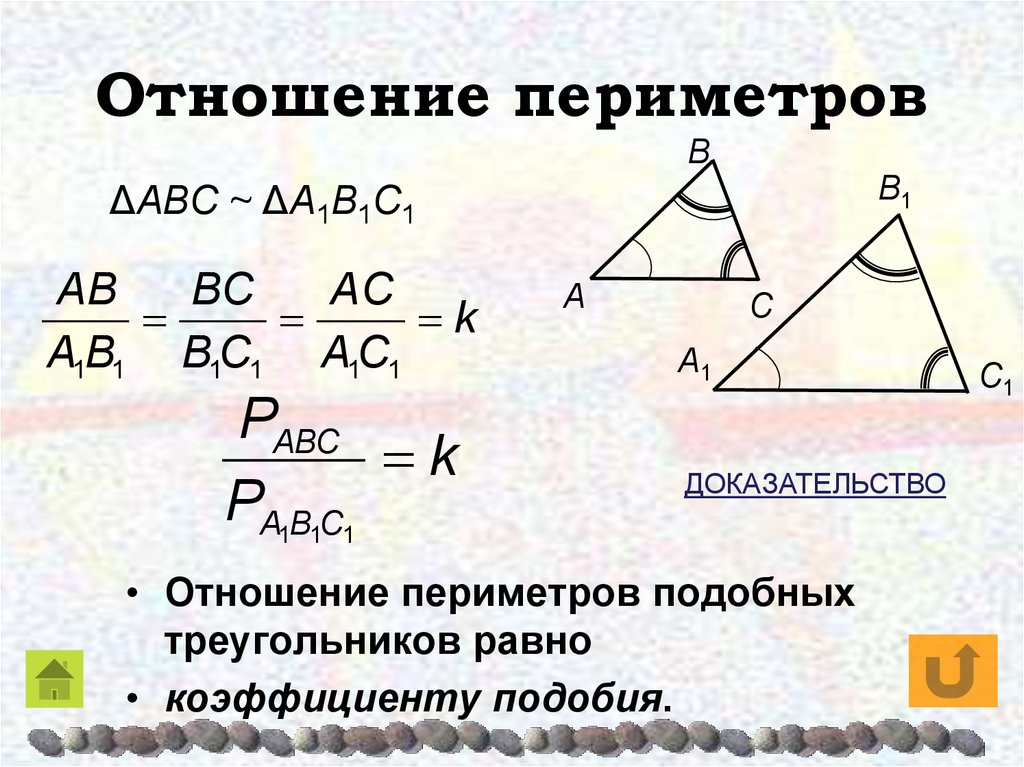
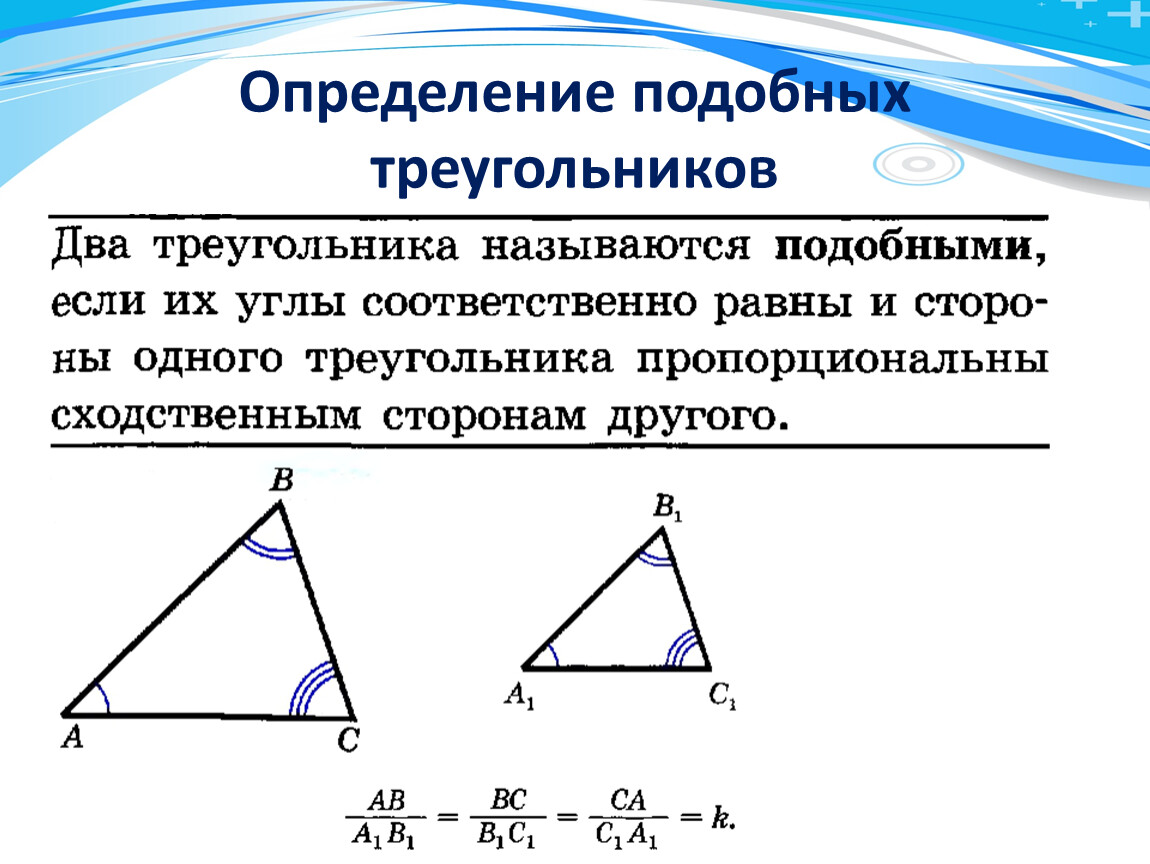
Обратите внимание на соотношение сторон подобных треугольников, так как периметры связаны именно с ними.
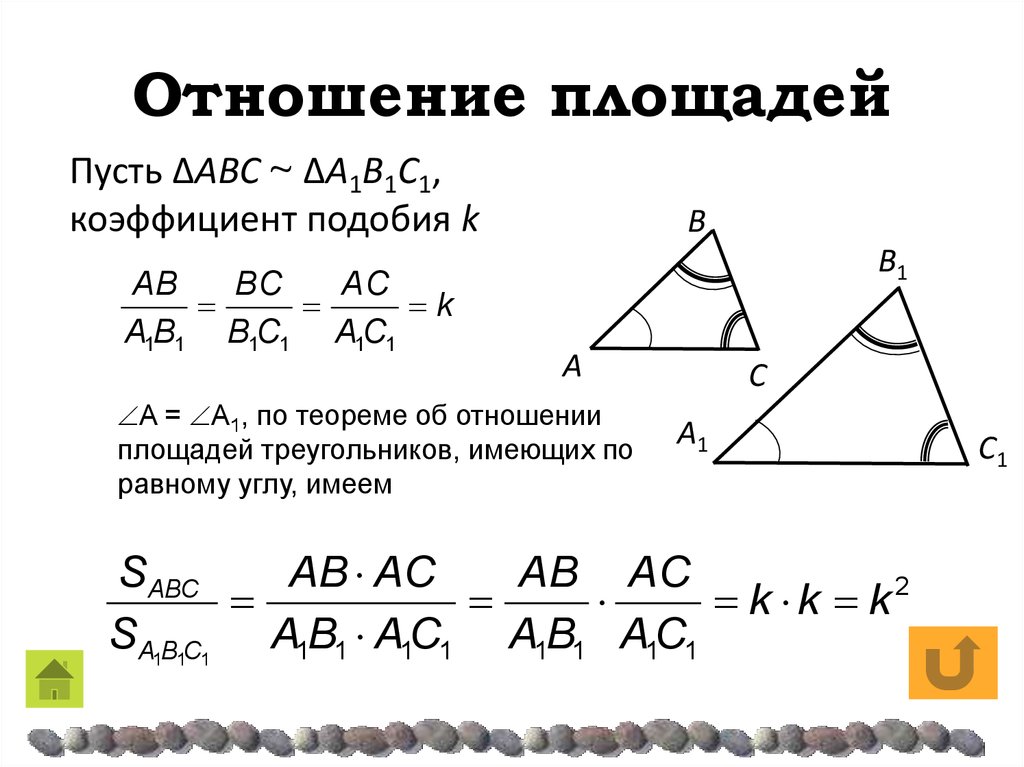
60. Отношение площадей подобных треугольников

Практикуйтесь в решении задач, включающих теорему о соотношении периметров, чтобы укрепить свои знания.
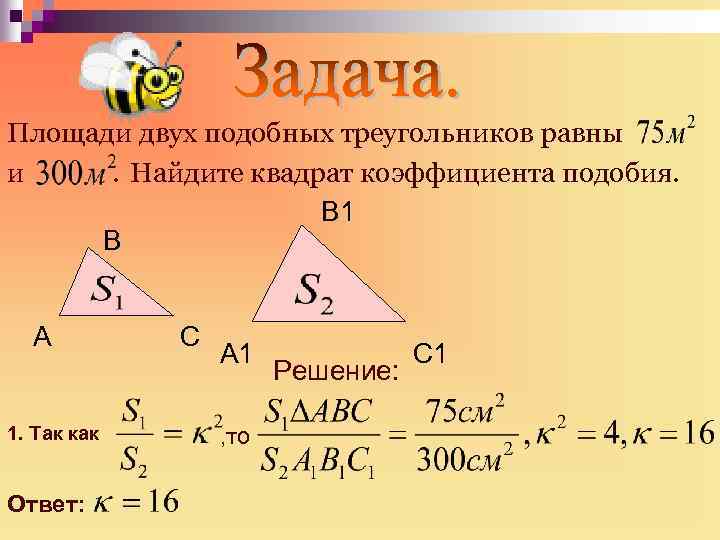
Используйте визуализации и чертежи, чтобы лучше понять пропорциональные отношения в треугольниках.
Подобные треугольники. Отношение периметров.
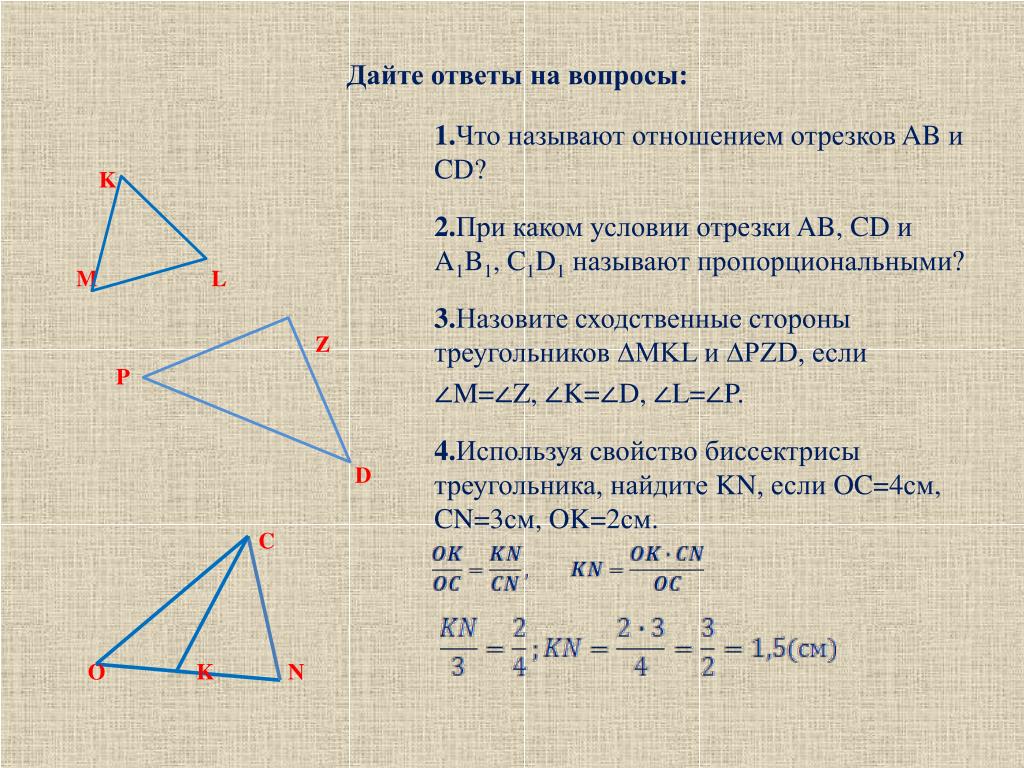
Запомните, что периметры подобных треугольников пропорциональны коэффициенту подобия.
№547. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.
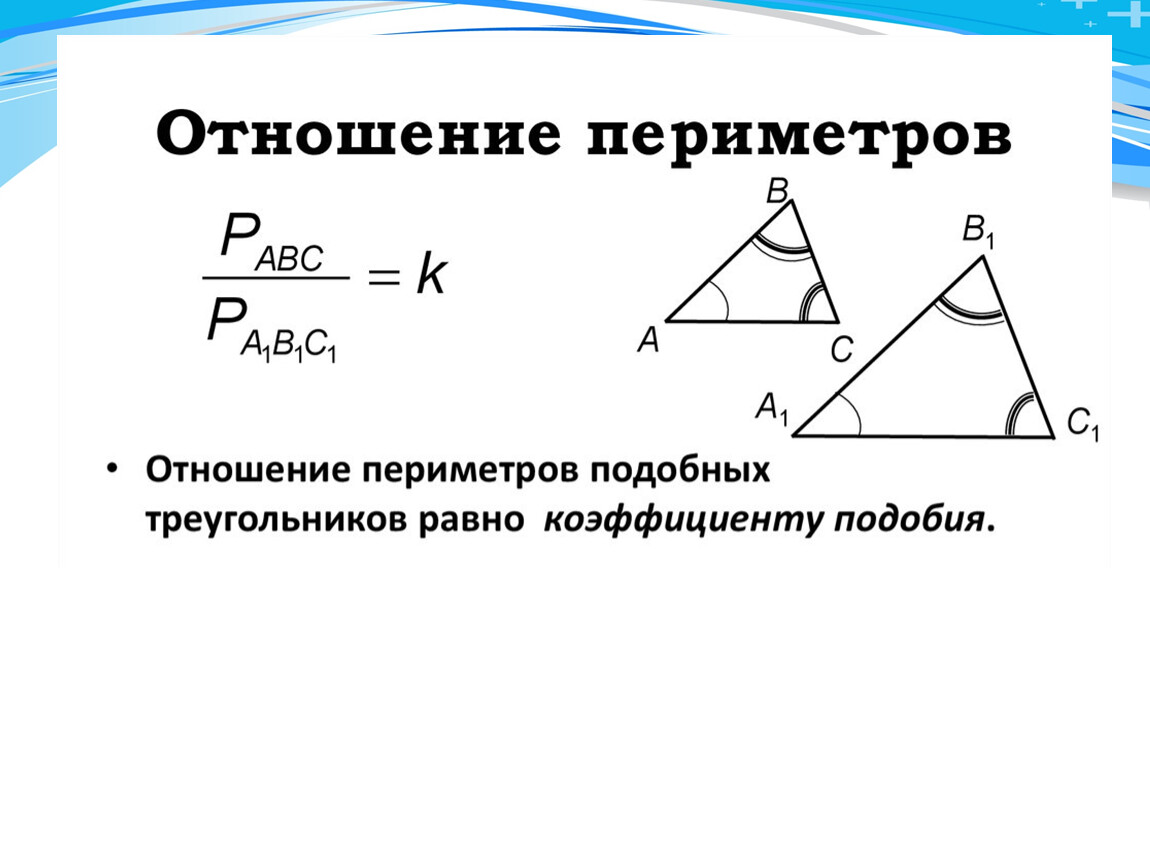

Проверяйте свои решения на точность, используя разные методы проверки.
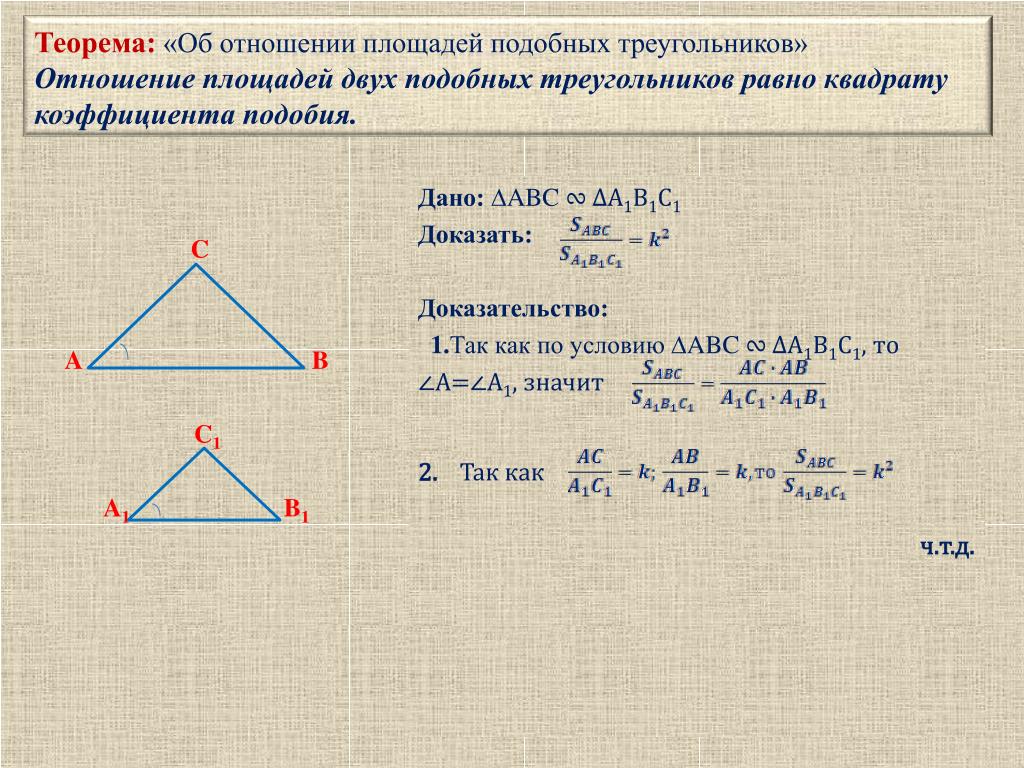
Изучите примеры из жизни, где применяется теорема о соотношении периметров подобных треугольников.
Консультируйтесь с преподавателями или одноклассниками, если возникают трудности с пониманием теоремы.
Геометрия 8 класс : Отношение площадей подобных треугольников

Создавайте свои собственные задачи и решайте их, чтобы развивать логическое мышление.

Используйте онлайн-ресурсы и учебные материалы для углубленного изучения темы.