Как дилемма заключённых объясняет стратегическое мышление
Теория игр является важной областью математики и экономики, которая помогает понять, как принимаются решения в условиях конкуренции и сотрудничества. Один из самых известных примеров - это дилемма заключённых, которая иллюстрирует, как рациональные игроки могут оказаться в ситуации, когда они не могут достичь оптимального результата из-за недоверия друг к другу.



Исследуйте основные понятия теории игр, такие как стратегии, выигрыши и равновесие Нэша.
Задача о Спящей красавице и монетке [Veritasium]

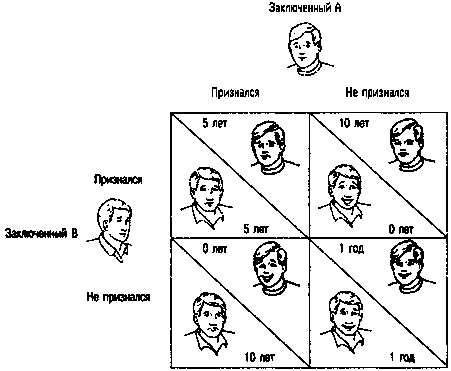
Рассмотрите классическую дилемму заключённых и попробуйте найти её решения с различными стратегиями.


Примените дилемму заключённых к реальным жизненным ситуациям, таким как бизнес-переговоры или политические соглашения.
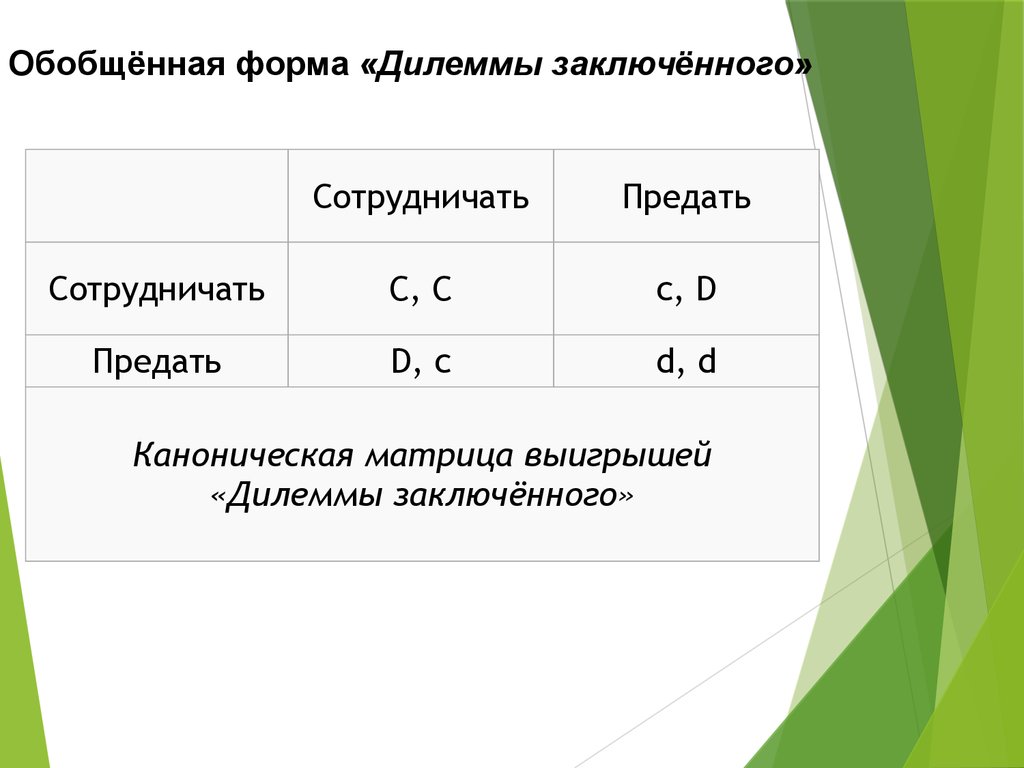
Дилемма заключённого и равновесие Нэша


Изучите другие известные игры в теории игр, такие как ястребы и голуби или координационная игра.
Используйте симуляции и компьютерные модели для анализа сложных игровых ситуаций.

Читайте научные статьи и книги по теории игр для углубленного понимания темы.

Участвуйте в семинарах и курсах по теории игр для обмена опытом и знаниями с другими энтузиастами.

Обратите внимание на применение теории игр в биологии, например, в моделях поведения животных.
Изучите примеры применения теории игр в социальных науках и экономике.
Основные теоремы в теории игр — Алексей Савватеев на ПостНауке


Практикуйтесь в решении задач и головоломок, основанных на теории игр, чтобы развить стратегическое мышление.