Как понять и использовать уравнение прямой на плоскости
В этой статье мы рассмотрим основные понятия и формулы, связанные с уравнением прямой на плоскости. Вы узнаете, как применять эти знания на практике и решать задачи различной сложности.


Определите основные параметры прямой: угол наклона и точку пересечения с осями координат.

Используйте уравнение вида y = kx + b для нахождения координат точек на прямой.
Как решить задачи по стереометрии? / Аксиомы стереометрии и следствия из них
Запомните, что коэффициент k определяет наклон прямой, а b – её пересечение с осью y.
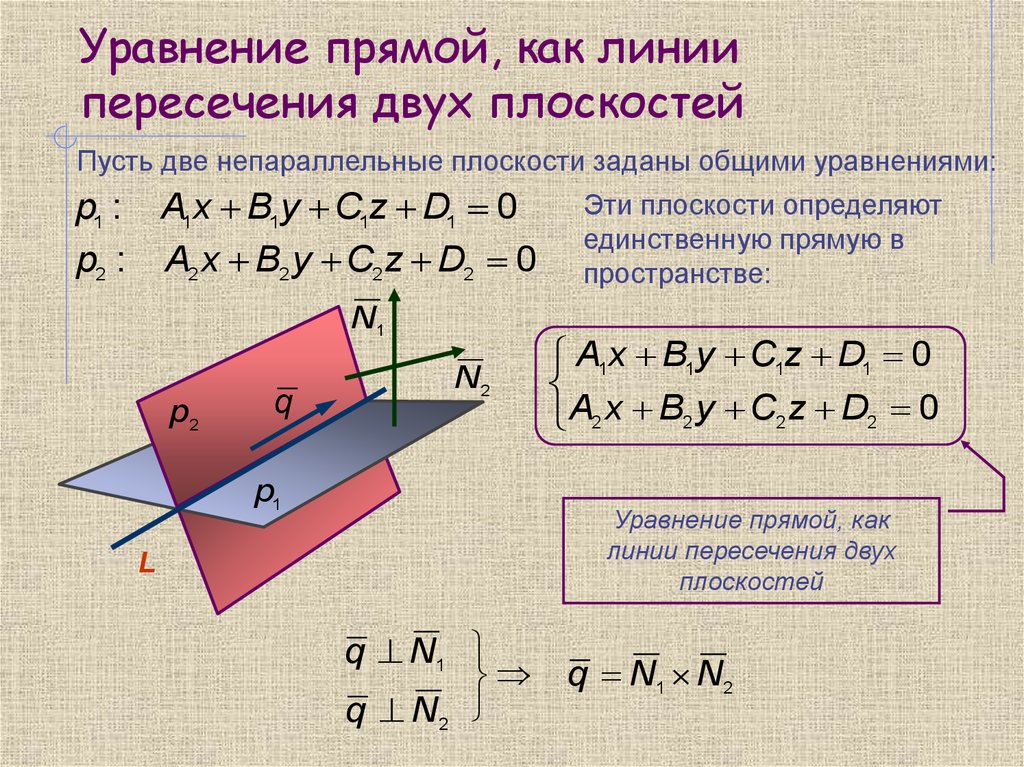
Уравнение прямой на плоскости
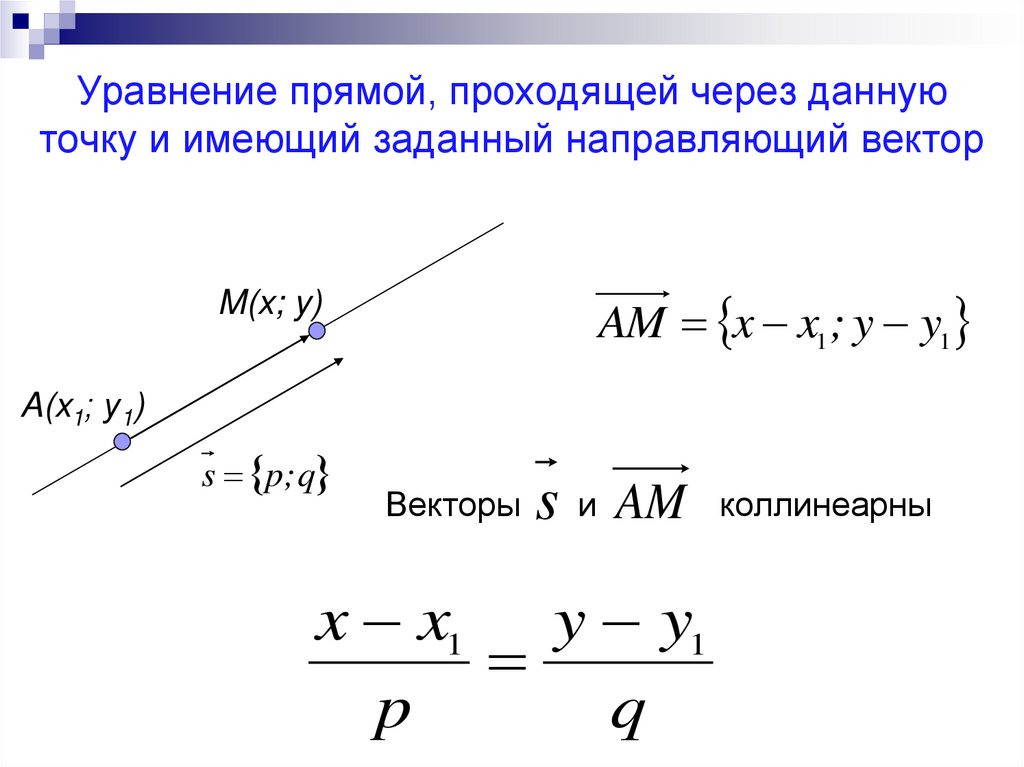
Для нахождения уравнения прямой через две точки используйте формулу (y - y1) = k(x - x1).

Чтобы найти угол между двумя прямыми, используйте формулу тангенса угла между ними: tan(φ) = |(k2 - k1) / (1 + k1k2)|.
УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 класс

Преобразуйте уравнение прямой к каноническому виду для упрощения вычислений.

Используйте метод подстановки для нахождения точки пересечения двух прямых.

Проверьте ваши расчеты с помощью графического построения на координатной плоскости.
Лекция 23. Виды уравнений прямой на плоскости.
Регулярно практикуйтесь в решении задач, чтобы лучше запомнить формулы и методы.
Уравнение прямой на плоскости

Изучайте дополнительные материалы и примеры для углубленного понимания темы.